iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s00500-022-07636-1
Fuzzy average edge connectivity with its application to communication networks | Soft Computing Skip to main content
Springer Nature Link
Log in

Fuzzy average edge connectivity with its application to communication networks

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

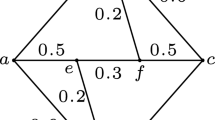
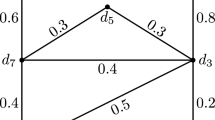
Abstract

Average edge connectivity is an important concept in the study of classical graph theory. However, it cannot be applied to the analysis of certain fuzzy problems. To address this problem, we introduce the definition of fuzzy average edge connectivity. In this paper, we study some properties of fuzzy average edge connectivity, including (1) fuzzy average edge connectivity of special fuzzy graphs, (2) fuzzy average edge connectivity of edge-deleted fuzzy subgraphs, (3) the bounds for fuzzy average edge connectivity of fuzzy graphs. In addition, we present algorithms on the connectivity parameter. Finally, practical applications verify the effectiveness of the theory and algorithms in communication networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

Enquiries about data availability should be directed to the authors.

References

  • Akram M (2019) m-Polar fuzzy graphs theory, methods and applications. Springer, Cham

    MATH  Google Scholar 

  • Akram M, Siddique S, Ahmad U (2021) Menger’s theorem for m-polar fuzzy graphs and application of m-polar fuzzy edges to road network. J Intell Fuzzy Syst 41(1):1553–1574

    Article  Google Scholar 

  • Akram M, Siddique S, Alharbi MG (2022) Clustering algorithm with strength of connectedness for m-polar fuzzy network models. Math Biosci Eng 19(1):420–455

    Article  MATH  Google Scholar 

  • Anjali N, Mathew S (2015) On blocks and stars in fuzzy graphs. J Intell Fuzzy Syst 28(4):1659–1665

    Article  MATH  Google Scholar 

  • Banerjee S (1991) An optimal algorithm to find the degrees of connectedness in an undirected edge-weighted graph. Pattern Recognit Lett 12(7):421–424

    Article  Google Scholar 

  • Bhutani KR (1989) On automorphisms of fuzzy graphs. Pattern Recognit Lett 9(3):159–162

    Article  MATH  Google Scholar 

  • Bhutani KR, Battou A (2003) On m-strong fuzzy graphs. Inf Sci 155(1–2):103–109

    Article  MATH  Google Scholar 

  • Bhutani KR, Rosenfeld A (2003) Fuzzy end nodes in fuzzy graphs. Inf Sci 152:323–326

    Article  MATH  Google Scholar 

  • Bhutani KR, Rosenfeld A (2003) Strong arcs in fuzzy graphs. Inf Sci 152:319–322

    Article  MATH  Google Scholar 

  • Ma JY, Li QG, Zhou XN (2021) Fuzzy edge connectivity and fuzzy local edge connectivity with applications to communication networks. Fuzzy Sets Syst 410:109–125

    Article  MATH  Google Scholar 

  • Manjusha OT, Sunitha MS (2019) Coverings, matchings and paired domination in fuzzy graphs using strong arcs. Iranian J Fuzzy Syst 16(1):145–157

    MATH  Google Scholar 

  • Mathew S, Sunitha MS (2009) Types of arcs in a fuzzy graph. Inf Sci 179(11):1760–1768

    Article  MATH  Google Scholar 

  • Mathew S, Sunitha MS (2010) Node connectivity and arc connectivity of a fuzzy graph. Inf Sci 180(4):519–531

    Article  MATH  Google Scholar 

  • Mathew S, Sunitha MS (2013) Strongest strong cycles and \(\theta -\)fuzzy graphs. IEEE Trans Fuzzy Syst 21(6):1096–1104

    Article  Google Scholar 

  • Mathew S, Anjali N, Mordeson JN (2018) Transitive blocks and their applications in fuzzy interconnection networks. Fuzzy Sets Syst 352:142–160

    Article  MATH  Google Scholar 

  • Mathew S, Mordeson JN, Malik DS (2018) Fuzzy Graph Theory. Springer

    Book  MATH  Google Scholar 

  • Mathew S, Yang HL, Mathew JK (2018) Saturation in fuzzy graphs. New Math Nat Comput 14:113–128

  • Nagoorgani A, Malarvizhi J (2009) Isomorphism properties of strong fuzzy graphs. Int J Algorithms, Comput Math 2(1):39–47

    Google Scholar 

  • Nagoorgani A, Radha K (2008) On regular fuzzy graphs. J Phys Sci 12:33–40

    MATH  Google Scholar 

  • Nagoorgani A, Akram M, Vijayalakshmi P (2016) Certain types of fuzzy sets in a fuzzy graph. Int J Mach Learn Cybern 7(4):573–579

    Article  Google Scholar 

  • Nair PS (1994) Triangle and parallelogram laws on fuzzy graphs. Pattern Recognit Lett 15:803–805

    Article  MATH  Google Scholar 

  • Poulik S, Ghorial G (2020) Certain indices of graphs under bipolar fuzzy environment with applications. Soft Comput 24:5119–5131

    Article  MATH  Google Scholar 

  • Poulik S, Ghorial G (2021) Determination of journeys order based on graph’s wiener absolute index with bipolar fuzzy information. Inf Sci 545:608–619

    Article  MATH  Google Scholar 

  • Poulik S, Ghorial G (2022) Applications of graph’s complete degree with bipolar fuzzy information. Complex Intell Syst 8:1115–1127

    Article  Google Scholar 

  • Poulik S, Ghorial G (2022) Estimation of most effected cycles and busiest network route based on complexity function of graph in fuzzy environmen. Artif Intell Rev 55:4557–4574

    Article  Google Scholar 

  • Poulik S, Ghorial G (2022) New concepts of inverse fuzzy mixed graphs and its application. Granular Comput 7:549–559

    Article  Google Scholar 

  • Poulik S, Ghorial G, Xin Q (2021) Pragmatic results in taiwan education system based ivfg and ivng. Soft Comput 25:711–724

    Article  Google Scholar 

  • Rosenfeld A (1975) Fuzzy graphs. fuzzy sets and their applications to cognitive and decision processes. Academic Press, New York

    Google Scholar 

  • Sarwar M, Akram M, Shahzadi S (2021) Bipolar fuzzy soft information applied to hypergraphs. Soft Comput 25:3417–3439

    Article  MATH  Google Scholar 

  • Sunitha MS, Vijayakumar A (1999) A characterization of fuzzy trees. Inf Sci 113(3–4):293–300

    Article  MATH  Google Scholar 

  • Sunitha MS, Vijayakumar A (2005) Blocks in fuzzy graphs. J Fuzzy Math 13(1):13–23

    MATH  Google Scholar 

  • Yeh RT, Bang SY (1975) Fuzzy relations, fuzzy graphs and their applications to clustering analysis .fuzzy sets and their applications. Academic Press, New York

    MATH  Google Scholar 

Download references

Acknowledgements

We thank the reviewers for their insightful comments. This work is supported by the Fundamental Research Program of Shanxi Province (No. 202103021223272) and Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (No. 2021L305), and Shanxi Scholarship Council of China (No.2020-122), and Research funding of Shanxi Province for outstanding talents (No. 20222003) and Taiyuan University of Science and Technology Scientific Research Initial Funding (No. 20202049).

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. School of Applied Science, Taiyuan University of Science and Technology, Taiyuan, 030024, People’s Republic of China

    Junye Ma & Jing Li

  2. School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan, 030024, People’s Republic of China

    Lin Li

Authors
  1. Junye Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lin Li.

Ethics declarations

Conflict of interest

There is no conflict of interest between the authors and the institute where the work has been carried out.

Ethical approval

The article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, J., Li, L. & Li, J. Fuzzy average edge connectivity with its application to communication networks. Soft Comput 27, 1367–1378 (2023). https://doi.org/10.1007/s00500-022-07636-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-07636-1

Keywords

Search

Navigation