iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s00422-004-0491-5
Optimal trajectory formation of constrained human arm reaching movements | Biological Cybernetics Skip to main content
Springer Nature Link
Log in

Optimal trajectory formation of constrained human arm reaching movements

  • Published:
Biological Cybernetics Aims and scope Submit manuscript

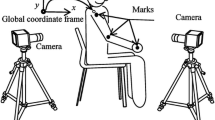
Abstract.

Opening a door, turning a steering wheel, and rotating a coffee mill are typical examples of human movements that are constrained by the physical environment. The constraints decrease the mobility of the human arm and lead to redundancy in the distribution of actuator forces (either joint torques or muscle forces). Due to this actuator redundancy, there is an infinite number of ways to form a specific arm trajectory. However, humans form trajectories in a unique way. How do humans resolve the redundancy of the constrained motions and specify the hand trajectory? To investigate this problem, we examine human arm movements in a crank-rotation task. To explain the trajectory formation in constrained point-to-point motions, we propose a combined criterion minimizing the hand contact force change and the actuating force change over the course of movement. Our experiments show a close matching between predicted and experimental data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abend W, Bizzi E, Morasso P (1982) Human arm trajectory formation. Brain 105:331–348

    Google Scholar 

  2. Baillieul J, Martin DP (1990) Resolution of kinematic redundancy. In: Brockett R (ed) Robotics Proceedings of the Symposia in Applied Mathematics, American Mathematical Society, 41:49–90

  3. Bernstein N (1967) The coordination and regulation of movements. Pergamon, London

  4. Chandler RF, Clause CE, McConville JT, Reynolds HM, Young JW (1975) Investigation of inertial properties of the human body, vol AMRL-TR-74-137. Wright Patterson Air Force Base, Ohio

  5. Chung W, Oh Y, Park J, Nenchev DN (1999) Analysis and control of kinematically redundant manipulators. In: Tutorial TS3, IEEE/RSJ International conference on intelligent robots and systems, Kyongju, South Korea

  6. Dornay M, Uno Y, Kawato M, Suzuki R (1996) Minimum muscle-tension change trajectories predicted by using a 17-muscle model of the monkey’s arm. J Motor Behav 28(2):83–100

    Google Scholar 

  7. Flash T, Hogan N (1985) The coordination of arm movement: a confirmed mathematical model. J Neurosci 5:1688–1703

    Google Scholar 

  8. Flash T, Hogan N, Richardson MJE (2003) Optimization principles in motor control. In: Arbib M (ed) Handbook of brain theory and neural networks, 2nd edn. MIT Press, Cambridge, MA, pp 827–831

  9. Gomi H, Osu R (1998) Task-dependent viscoelasticity of human multijoint arm and its spatial characteristics for interaction with environments. J Neurosci 18(21):8965–8978

    Google Scholar 

  10. Harris CM (1998) On the optimal control of behaviour: a stochastic perspective. J Neurosci Meth 83:73–88

    Google Scholar 

  11. Harris CM, Wolpert DW (1998) Signal-dependent noise determines motor planning. Nature 394:780–784

    Google Scholar 

  12. Hoff B, Arbib MA (1992) A model of the effects of speed, accuracy, and perturbation on visually guided reaching. Exp Brain Res 22:285–306

    Google Scholar 

  13. Ito K, Tsuji K, Sugino M (1991) Impedance regulation in human movements during a rotation task. J Robot Mechatron pp 44–51

  14. Jordan MI, Flash T, Arnon Y (1994) A model of the learning of arm trajectories from spatial deviations. J Cogn Neurosci 6:359–376

    Google Scholar 

  15. Kashima T, Isurugi Y (1998) Trajectory formation based on physiological characteristics of skeletal muscles. Biol Cybern 78:413–422

    Google Scholar 

  16. Kashima T, Isurugi Y, Shima M (2000) Analysis of a muscular control system in human movements. Biol Cybern 82:123–131

    Google Scholar 

  17. Kawato M (1996) Trajectory formation in arm movements: Minimization principles and procedures. In: Zelaznik H (ed) Advances in motor learning and control. Human Kinetics, Champaign, IL, pp 225–259

  18. Kawato M (1999) Internal models for motor control and trajectory planning. Curr Opin Neurobiol 9:718–727

    Google Scholar 

  19. Kawato M, Maeda Y, Uno Y, Suzuki R (1990) Trajectory formation of arm movement by cascade neural network model based on minimum torque-change criterion. Biol Cybern 62:275–288

    Google Scholar 

  20. Kitazawa S (2002) Optimization of goal-directed movements in the cerebellum: a random walk hypothesis. Neurosci Res 43(4):289–294

    Google Scholar 

  21. Luo ZW, Yamakita M, Iwakoshi K, Ito M (1995) Compliance control considering robot’s manipulability. Trans Soc Instrum Contr Eng 31:1534–1536

    Google Scholar 

  22. Maeda H, Miyaji K (1994) Task understanding of the crank turning. In: IEEE/RSJ conference on intelligent robots and systems, 2:958–965

  23. Mason M (1981) Compliance and force control for computer-controlled manipulators. IEEE Trans Syst Man Cybern 11(6):418–432

    Google Scholar 

  24. Meek SG, Wood JE, Jacobsen SC (1990) Model-based, multi-muscle EMG control of upper-extremity Prostheses. In: Winters JM, Woo SL-Y (eds) Multiple muscle system: biomechanics and movement organization. Springer, Berlin Heidelberg New York, pp 360–376

  25. Morasso P (1981) Spatial control of arm movements. Exp Brain Res 42:223–227

    Google Scholar 

  26. Nijhof EJ, Kouwenhoven E (2000) Simulation of Multijoint arm Movements. In: Winters JM, Crago PE (eds) Biomechanics and neural control of posture and movement. Springer, Berlin Heidelberg New York, pp 363–372

  27. Ohta K, Svinin MM, Luo ZW, Hosoe S (2003) Dealing with constraints: Optimal trajectories of the constrained human arm movements. In: Proceedings of the XVII IMEKO world congress, tc-18: measurement in human functions, Dubrovnik, Croatia, pp 2059–2064

  28. Russell D, Hogan N (1989) Dealing with constraints: A biomechanical approach. In: Proceedings of the IEEE Engineering in Medicine and Biological Society 11th Annual Conference, pp 892–893

  29. Scheidt R, Dingwell J, Mussa-Ivaldi F (2001) Learning to move amid uncertainty. J Neurophysiol 86:971–985

    Google Scholar 

  30. Schwartz A, Polak E, Chen Y (1997) RIOTS95: A matlab toolbox for solving optimal control problems, version 1.0, User Manual, Stanford University

  31. Shadmehr R, Mussa-Ivaldi F (1994) Adaptive representation of dynamics during learning of a motor task. J Neurosci 14:3208–3224

    Google Scholar 

  32. Svinin MM, Ohta K, Luo ZW, Hosoe S (2001) Mathematical analysis of the crank turning task. In: International symposium on measurement, analysis and modeling of human functions (ISHF 2001), Sapporo, pp 346–352

  33. Thoroughman KA, Shadmehr R (2000) Learning of action through adaptive combination of motor primitives. Nature 407:742–747

    Google Scholar 

  34. Todorov E, Jordan M (2002) Optimal feedback control as a theory of motor coordination. Nat Neurosci 5:1226–1235

    Google Scholar 

  35. Todorov E, Jordan MI (2003) A minimal intervention principle for coordinated movement. In: Becker S, Thrun S, Obermayer K (eds) Advances in neural information processing systems, vol 15. MIT Press, Cambridge, MA, pp 27–34

  36. Uno Y, Kawato M, Suzuki R (1989) Formation and control of optimal trajectory in human multijoint arm movement. Biol Cybern 61:89–101

    Google Scholar 

  37. Uno M, Suzuki R, Kawato M (1989) Minimum muscle tension change model which produces human arm movement. In: Proceedings of the 4th symposium on biological and physiological engineering, pp 299–302

  38. Wolpert DM, Ghahramani Z, Jordan MI (1995) Are arm trajectories planned in kinematic or dynamic coordinate? An adaptation study. Exp Brain Res 103:460–470

    Google Scholar 

  39. Zefran M (1996) Continuous methods for motion planning. PhD thesis, University of Pennsylvania

Download references

Author information

Authors and Affiliations

  1. Sensorimotor Coordination, Max Planck Institute for Human Cognitive and Brain Sciences, Munich, Germany

    Ken Ohta & Rafael Laboissière

  2. Bio-Mimetic Control Research Center, RIKEN, Nagoya, Japan

    Mikhail M. Svinin, ZhiWei Luo & Shigeyuki Hosoe

  3. Faculty of Engineering, Nagoya University, Nagoya, Japan

    Shigeyuki Hosoe

Authors
  1. Ken Ohta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mikhail M. Svinin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. ZhiWei Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shigeyuki Hosoe
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Rafael Laboissière
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ken Ohta.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ohta, K., Svinin, M., Luo, Z. et al. Optimal trajectory formation of constrained human arm reaching movements. Biol. Cybern. 91, 23–36 (2004). https://doi.org/10.1007/s00422-004-0491-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00422-004-0491-5

Keywords

Search

Navigation