iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s00332-010-9090-x
Propagation Failure Along Myelinated Nerves | Journal of Nonlinear Science Skip to main content
Springer Nature Link
Log in

Propagation Failure Along Myelinated Nerves

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

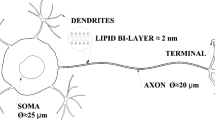
Abstract

Propagation of traveling pulses in the myelinated Hodgkin–Huxley model is studied. The nerve impulse is a traveling wave with two components. At the Ranvier nodes, it behaves as a discrete traveling pulse. Wave motion through the internodal regions is then driven by this traveling pulse. We give analytical characterizations of the parameter ranges for which nerve impulses fail to propagate by exploiting time scale separation and the active node approximation, which reduces the dynamics of infinite fibers to the evolution of a few nodes. Simple recipes to predict the speed of the impulses and the widths of their peaks are also given. Predictions are in good agreement with the information provided by numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Anderson, A.R.A., Sleeman, B.D.: Wave front propagation and its failure in coupled systems of discrete bistable cells modelled by FitzHugh-Nagumo dynamics. Int. J. Bifurc. Chaos 5, 63–74 (1995)

    Article  MATH  Google Scholar 

  • Beeler, G.W., Reuter, H.: Reconstruction of the action potential of ventricular myocardial fibres. J. Physiol. 268, 177–210 (1977)

    Google Scholar 

  • Bell, J., Costner, C.: Threshold behavior and propagation for nonlinear differential-difference systems motivated by modeling myelinated axons. Q. Appl. Math. 42, 1–13 (1984)

    MATH  Google Scholar 

  • Binczak, S., Eilbeck, J.C., Scott, A.C.: Ephaptic coupling of myelinated nerve fibers. Physica D 148, 159–174 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • Carpio, A.: Asymptotic construction of pulses in the Hodgkin–Huxley model for myelinated nerves. Phys. Rev. E 72, 011905 (2005a)

    Article  MathSciNet  Google Scholar 

  • Carpio, A.: Wave trains, self-oscillations and synchronization in discrete media. Physica D 207, 117–136 (2005b)

    Article  MathSciNet  MATH  Google Scholar 

  • Carpio, A., Bonilla, L.L.: Wave front depinning transition in discrete one dimensional reaction-diffusion systems. Phys. Rev. Lett. 86, 6034–6037 (2001)

    Article  Google Scholar 

  • Carpio, A., Bonilla, L.L.: Depinning transitions in discrete reaction-diffusion equations. SIAM J. Appl. Math. 63, 1056–1082 (2003a)

    Article  MathSciNet  MATH  Google Scholar 

  • Carpio, A., Bonilla, L.L.: Pulse propagation in discrete systems of excitable cells. SIAM J. Appl. Math. 63(2), 619–635 (2003b)

    Article  MathSciNet  Google Scholar 

  • Carpio, A., Chapman, S.J., Hastings, S., Mcleod, J.B.: Wave solutions for a discrete reaction-diffusion equation. Eur. J. Appl. Math. 11, 399–412 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  • Casten, R.G., Cohen, H., Lagerstrom, P.A.: Perturbation analysis of an approximation to the Hodgkin–Huxley theory. Q. Appl. Math. 4, 365–402 (1975)

    Google Scholar 

  • Cole, K.S.: Membranes, Ions and Impulses. University of California Press, Berkeley (1968)

    Google Scholar 

  • Coombes, S., Hinch, R., Timofeeva, Y.: Receptors, sparks and waves in a fire-diffuse-fire framework for calcium release. Prog. Biophys. Mol. Biol. 85, 197–216 (2003)

    Article  Google Scholar 

  • Fáth, G.: Propagation failure of traveling waves in a discrete bistable medium. Physica D 116, 176–180 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  • FitzHugh, R.: Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1, 445–466 (1961)

    Article  Google Scholar 

  • FitzHugh, R.: Computation of impulse initiation and saltatory conduction in a myelinated nerve fiber. Biophys. J. 2, 11–21 (1962)

    Article  MathSciNet  Google Scholar 

  • Goldman, L., Albus, J.S.: Computation of impulse conduction in myelinated fibres: Theoretical basis of the velocity-diameter relation. Biophys. J. 8, 596–607 (1968)

    Article  Google Scholar 

  • Hodgkin, A.L., Huxley, A.F.: A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544 (1952)

    Google Scholar 

  • Keener, J.P.: Waves in excitable media. SIAM J. Appl. Math. 39, 528–548 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  • Keener, J.P.: Propagation failure in coupled systems of discrete excitable cells. SIAM J. Appl. Math. 47, 317–334 (2000)

    Article  MathSciNet  Google Scholar 

  • Keener, J.P., Sneyd, J.: Mathematical Physiology. Springer, Berlin (1998)

    MATH  Google Scholar 

  • Mallet-Paret, J.: The global structure of traveling waves in spatially discrete dynamical systems. J. Dyn. Differ. Equ. 11, 1–47 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  • Markin, V.S., Chimadzhev, Yu.A.: On the propagation of an excitation for one model of a nerve fiber. Biophys. J. 12, 1032–1040 (1967)

    Google Scholar 

  • Morris, C., Lecar, H.: Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 35, 193–213 (1981)

    Article  Google Scholar 

  • Moore, J.W., Joyner, R.W., Brill, M.H., Waxman, S.D., Najar-Joa, M.: Simulations of conduction in uniform myelinated fibers: Relative sensitivity to changes in nodal and internodal parameters. Biophys. J. 21, 147–160 (1978)

    Article  Google Scholar 

  • Muratov, C.B.: A quantitative approximation scheme for traveling wave solutions in the Hodgkin–Huxley model. Biophys. J. 79, 2893–2901 (2000)

    Article  Google Scholar 

  • Nagumo, J., Arimoto, S., Yoshizawa, S.: An active pulse transmission line simulating nerve axon. Proc. Inst. Radio Eng. 50, 2061–2070 (1962)

    Google Scholar 

  • Pickard, W.F.: On the propagation of the nervous impulse down medullated and unmedullated fibers. J. Theor. Biol. 11, 30–40 (1966)

    Article  Google Scholar 

  • Pluchino, S., Quattrini, A., Brambilla, E., et al.: Injection of adult neurospheres induces recovery in a chronic model of multiple sclerosis. Nature 422, 688–694 (2003)

    Article  Google Scholar 

  • Ponce Dawson, S., Keizer, J., Pearson, J.E.: Fire-diffuse-fire model of dynamics of intracellular calcium waves. Proc. Natl. Acad. Sci. USA 96, 6060–6063 (1999)

    Article  Google Scholar 

  • Rinzel, J., Keller, J.B.: Traveling wave solutions of a nerve conduction equation. Biophys. J. 13, 1313–1337 (1973)

    Article  Google Scholar 

  • Rushton, W.A.H.: A theory of the effects of fibre size in medullated nerve. J. Physiol. 115, 101–122 (1951)

    Google Scholar 

  • Scott, A.C.: The electrophysics of a nerve fiber. Rev. Mod. Phys. 47, 487–533 (1975)

    Article  Google Scholar 

  • Scott, A.C.: Neuroscience. Springer, Berlin (2002)

    MATH  Google Scholar 

  • Struijk, J.J.: The extracellular potential of a myelinated nerve fiber in an unbounded medium and in nerve cuff models. Biophys. J. 72, 2457–2469 (1997)

    Article  Google Scholar 

  • Timofeeva, Y.: Travelling waves in a model of quasi-active dendrites with active spines. Physica D 239, 494–503 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  • Tonnelier, A.: The McKean’s caricature of the FitzHugh-Nagumo model: Traveling pulses in discrete diffusive medium. Phys. Rev. E 67, 036105 (2003)

    Article  MathSciNet  Google Scholar 

  • Zinner, B.: Existence of traveling wave front solutions for the discrete Nagumo equation. J. Differ. Equ. 96, 1–27 (1992)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática Aplicada, Universidad Complutense de Madrid, Madrid, 28040, Spain

    A. Carpio & I. Peral

Authors
  1. A. Carpio
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. Peral
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Carpio.

Additional information

Communicated by P.K. Maini.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Carpio, A., Peral, I. Propagation Failure Along Myelinated Nerves. J Nonlinear Sci 21, 499–520 (2011). https://doi.org/10.1007/s00332-010-9090-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00332-010-9090-x

Keywords

Mathematics Subject Classification (2000)

Search

Navigation