Abstract
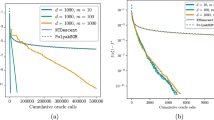
In this paper a new algorithm for minimizing locally Lipschitz functions is developed. Descent directions in this algorithm are computed by solving a system of linear inequalities. The convergence of the algorithm is proved for quasidifferentiable semismooth functions. We present the results of numerical experiments with both regular and nonregular objective functions. We also compare the proposed algorithm with two different versions of the subgradient method using the results of numerical experiments. These results demonstrate the superiority of the proposed algorithm over the subgradient method.
Similar content being viewed by others
References
Bagirov AM and Gasanov AA (1995). A method of approximating a quasidifferential. J Comput Math Math Phys 35(4): 403–409
Bagirov AM (1998). Discrete gradient as applied to the minimization of Lipschitzian functions. J Comput Math Math Phys 38(10): 1556–1565
Bagirov AM (1999). Minimization methods for one class of nonsmooth functions and calculation of semi-equilibrium prices. In: Eberhard, A et al (eds) Progress in optimization: contribution from Australasia, pp 147–175. Kluwer, Dordrecht
Bagirov AM (2002). A method for minimizing of quasidifferentiable functions. Optim Methods Software 17(1): 31–60
Bagirov AM (2003). Continuous subdifferential approximations and their applications. J Math Sci 115(5): 2567–2609
Bagirov AM, Ghosh M and Webb D (2006). A derivative-free method for linearly constrained nonsmooth optimization. J Ind Manage Optim 2(3): 319–338
Bagirov AM, Karasozen B, Sezer M (2008) Discrete gradient method: a derivative free method for nonsmooth optimization. J Optim Theory Appl 136(3)
Bagirov AM, Rubinov AM, Soukhoroukova NV and Yearwood J (2003). Supervised and unsupervised data classification via nonsmooth and global optimisation. TOP: Spanish Oper Res J 11(1): 1–93
Bagirov AM and Yearwood J (2006). A new nonsmooth optimization algorithm for minimum sum-of-squares clustering problems. Eur J Oper Res 170(2): 578–596
Bertsekas DP (1999). Nonlinear programming, 2nd edn. Athena Scientific, Nashua
Burke JV, Lewis AS and Overton ML (2005). A robust gradient sampling algorithm for nonsmooth, nonconvex optimization. SIAM J Optim 15(3): 751–779
Clarke FH (1983). Optimization and nonsmooth analysis. Wiley, New York
Demyanov VF and Rubinov AM (1995). Constructive nonsmooth analysis. Peter Lang, Frankfurt am Main
Frangioni A (2002). Generalized bundle methods. SIAM J Optim 113(1): 117–156
Golikov AI and Evtushenko YuG (2001). A new method for solving systems of linear equalities and inequalities. Dokl Math 64(3): 370–373
Gaudioso M and Monaco MF (1982). A bundle type approach to the unconstrained minimization of convex nonsmooth functions. Math Program 23: 216–226
Hiebert K (1980). Solving systems of linear equations and inequalities. SIAM J Numer Anal 17(3): 447–464
Hiriart-Urruty JB and Lemarechal C (1993). Convex analysis and minimization algorithms, vol 1, 2. Springer, New York
Kiwiel KC (1985). Methods of descent for nondifferentiable optimization. Lecture Notes in Mathematics, vol 1133. Springer, Berlin
Luksan L, Vlcek J (2000) Test problems for nonsmooth unconstrained and linearly constrained optimization, Technical Report No. 78, Institute of Computer Science, Academy of Sciences of the Czech Republic
Makela MM and Neittaanmaki P (1992). Nonsmooth optimization. World Scientific, Singapore
Mifflin R (1977a). Semismooth and semiconvex functions in constrained optimization. SIAM J Control Optim 15(6): 959–972
Mifflin R (1977b). An algorithm for constrained optimization with semismooth functions.. Math Oper Res 2: 191–207
Polak E and Royset JO (2003). Algorithms for finite and semi-infinite min–max–min problems using adaptive smoothing techniques. J Optim Theory Appl 119(3): 421–457
Polyak B (1985). Introduction to optimization. Optim Software, New York
Shor NZ (1985). Minimization methods for non-differentiable functions. New York, Berlin
Wolfe PH (1975). A method of conjugate subgradients of minimizing nondifferentiable convex functions. Math Program Study 3: 145–173
Zowe J (1985). Nondifferentiable optimization: a motivation and a short introduction into the subgradient and the bundle concept. In: Schittkowski, K (eds) Computational mathematical programming. NATO SAI Series, vol 15, pp 323–356. Springer, New York
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bagirov, A., Ganjehlou, A.N. An approximate subgradient algorithm for unconstrained nonsmooth, nonconvex optimization. Math Meth Oper Res 67, 187–206 (2008). https://doi.org/10.1007/s00186-007-0186-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-007-0186-5