iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s00034-012-9439-5
Stabilization of a Class of Switched Stochastic Systems with Time Delays Under Asynchronous Switching | Circuits, Systems, and Signal Processing Skip to main content
Springer Nature Link
Log in

Stabilization of a Class of Switched Stochastic Systems with Time Delays Under Asynchronous Switching

  • Short Paper
  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

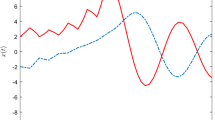
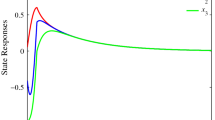
This paper addresses stabilization problem for a class of switched stochastic systems with time delays by using piecewise Lyapunov–Krasovskii functional method. Asynchronous switching means the switching of the controller has a time delay to the switching of the system. We provide a set of Lyapunov–Krasovskii-type sufficient conditions for establishing the mean-square exponential stability. The mean-square exponential stability condition for the resulting closed-loop system is firstly derived by further allowing the Lyapunov–Krasovskii functional to increase during the running time of the active subsystem with the mismatched controller. Then, the corresponding solvability condition for stabilizing controllers is established. Finally, we present an example to show the effectiveness of the developed theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. B. Øksendal, Stochastic Differential Equations: an Introduction with Applications (Springer, New York, 1989)

    Google Scholar 

  2. M.S. Branicky, Multiple Lyapunov functions and other analysis tools for switched and hybrid systems. IEEE Trans. Autom. Control 43(4), 475–482 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  3. H.J. Gao, C.H. Wang, A delay-dependent approach to robust H ∞ and L 2–L ∞ filtering for a class of uncertain nonlinear time-delayed systems. IEEE Trans. Autom. Control 48(9), 1661–1666 (2003)

    Article  Google Scholar 

  4. L. Hetel, J. Daafouz, C. Iung, Stability analysis for discrete time switched systems with temporary uncertain switching signal, in Proceeding of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA (2007), pp. 12–14

    Google Scholar 

  5. D. Liberzon, A.S. Morse, Basic problems in stability and design of switched systems. IEEE Control Syst. 19(5), 59–70 (1999)

    Article  Google Scholar 

  6. H. Lin, P.J. Antsaklis, Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans. Autom. Control 54(2), 308–322 (2009)

    Article  MathSciNet  Google Scholar 

  7. X. Su, P. Shi, L. Wu, Y. Song, A novel approach to filter design for T–S fuzzy discrete-time systems with time-varying delay. IEEE Trans. Fuzzy Syst. (2012). doi:10.1109/TFUZZ.2012.2196522

    Google Scholar 

  8. X.M. Sun, J. Zhao, J. David, Stability and L 2-gain analysis for switched delay systems: a delay-dependent method. Automatica 42(10), 1769–1774 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  9. X.M. Sun, G.P. Liu, D. Rees, W. Wang, Delay-dependent stability for discrete systems with large delay sequence based on switching techniques. Automatica 44(11), 2902–2908 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  10. X.M. Sun, G.P. Liu, D. Rees, W. Wang, Stability of systems with controller failure and time-varying delay. IEEE Trans. Autom. Control 53(10), 2391–2396 (2008)

    Article  MathSciNet  Google Scholar 

  11. L. Vu, M.A. Kristi, Stability of time-delay feedback switched linear systems. IEEE Trans. Autom. Control 55(10), 2385–2389 (2010)

    Article  Google Scholar 

  12. Y.E. Wang, X.M. Sun, J. Zhao, Stabilization of a class of switched stochastic systems with asynchronous switching, in The 24th Chinese Control and Decision Conference, Taiyuan, China (2012), pp. 552–556

    Chapter  Google Scholar 

  13. Z. Wang, H. Qiao, Robust filtering for bilinear uncertain stochastic discrete-time systems. IEEE Trans. Signal Process. 50(3), 560–567 (2002)

    Article  MathSciNet  Google Scholar 

  14. Z. Wang, H. Qiao, K.J. Burnham, On stabilization of bilinear uncertain time-delay stochastic systems with Markovian jumping parameters. IEEE Trans. Autom. Control 47(4), 640–646 (2002)

    Article  MathSciNet  Google Scholar 

  15. L.G. Wu, D.W.C. Ho, C.W. Li, Stabilization and performance synthesis for switched stochastic systems. IET Control Theory Appl. 4(10), 2010 (1877–1888)

    MathSciNet  Google Scholar 

  16. L.G. Wu, D.W.C. Ho, Reduced-order L 2–L ∞ filtering for a class of nonlinear switched stochastic systems. IET Control Theory Appl. 3(5), 493–508 (2009)

    Article  MathSciNet  Google Scholar 

  17. L.G. Wu, D.W.C. Ho, Sliding mode control of singular stochastic hybrid systems. Automatica 46(4), 779–783 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. L.G. Wu, D.W.C. Ho, C.W. Li, Sliding mode control of switched hybrid systems with stochastic perturbation. Syst. Control Lett. 60(8), 531–539 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  19. L.G. Wu, D.W.C. Ho, Fuzzy filter design for nonlinear Itô stochastic systems with application to sensor fault detection. IEEE Trans. Fuzzy Syst. 17(1), 233–242 (2009)

    Article  Google Scholar 

  20. L.G. Wu, W.X. Zheng, L 2–L ∞ Control of nonlinear fuzzy Itô stochastic delay systems via dynamic output feedback. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 39(5), 1308–1315 (2009)

    Article  MathSciNet  Google Scholar 

  21. Z.R. Xiang, C.Y. Liang, Q.W. Chen, Robust L 2–L ∞ filtering for switched systems under asynchronous switching. Commun. Nonlinear Sci. Numer. Simul. 16(8), 3303–3318 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  22. Z.R. Xiang, R.H. Wang, Robust control for uncertain switched non-linear systems with time delay under asynchronous switching. IET Control Theory Appl. 3(8), 1041–1050 (2008)

    Article  MathSciNet  Google Scholar 

  23. G.M. Xie, L. Wang, Stabilization of switched linear systems. J. Math. Anal. Appl. 305(1), 277–290 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  24. S. Xu, T. Chen, Robust H ∞ control for uncertain stochastic systems with state delay. IEEE Trans. Autom. Control 47(12), 2089–2094 (2002)

    Article  Google Scholar 

  25. S. Xu, T. Chen, H ∞ output feedback control for uncertain stochastic systems with time-varying delays. Automatica 40(12), 2091–2098 (2004)

    MathSciNet  MATH  Google Scholar 

  26. L.X. Zhang, P. Shi, Stability, ℓ 2-gain and asynchronous H ∞ control of discrete-time switched systems with average dwell time. IEEE Trans. Autom. Control 54(9), 2193–2200 (2009)

    Google Scholar 

  27. L.X. Zhang, H.J. Gao, Asynchronously switched control of switched linear systems with average dwell time. Automatica 46(5), 953–958 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. J. Zhao, D.J. Hill, On stability, L 2-gain and H ∞ control for switched systems. Automatica 44(5), 1220–1232 (2008)

    Article  MathSciNet  Google Scholar 

  29. J. Zhao, D.J. Hill, Passivity theory for switched systems. IEEE Trans. Autom. Control 53(4), 941–953 (2008)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the NSFC under Grants 61174058 and 61004020, and the Program for New Century Excellent Talents in University NCET-09-0257.

Author information

Authors and Affiliations

  1. The State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, 110819, China

    Yue-E Wang & Jun Zhao

  2. The School of Control Science and Engineering, Dalian University of Technology, Dalian, 116024, China

    Xi-Ming Sun

Authors
  1. Yue-E Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xi-Ming Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jun Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yue-E Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, YE., Sun, XM. & Zhao, J. Stabilization of a Class of Switched Stochastic Systems with Time Delays Under Asynchronous Switching. Circuits Syst Signal Process 32, 347–360 (2013). https://doi.org/10.1007/s00034-012-9439-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-012-9439-5

Keywords

Search

Navigation