A modularity-maximization-based approach for detecting multi-communities in social networks

Abstract

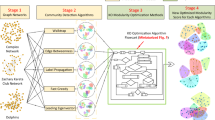
The modularity is a widely-used objective function to determine communities from a given network. The leading eigenvector method is a popular solution that applies the first eigenvector to determine the communities. The low computation cost is the major advantage of the leading eigenvector method. However, the leading eigenvector method only can split a network into two communities. To detect multiple communities, the modularity maximization is transformed to the vector partition problem (VPP). We propose an algorithm which is called as the partition at polar coordinate protocol (PPCP) to solve the VPP problem. The goal of PPCP is to find non-overlapping vertex vector sets so as to maximize the quadratic sum of the norms of community vectors. The proposed PPCP has two steps to determine the communities that are the network structure analysis and the community determination. During the network structure analysis, we obtain following issues. First, the vertex vectors belong to different communities can be separated by the distribution angles. Second, a node with a higher degree corresponds to a vertex vector with a larger norm. So, we propose three refinement functions including the noise reduction, the common-friends model and the strong connectivity hypothesis to improve the accuracy of PPCP. In our simulations, PPCP detects communities more precisely than Fine-tuned algorithm especially in the network with the weak structure. Moreover, the proposed refinement functions can capture the special properties of the network. So, PPCP with refinement functions performs much better than Fine-tuned algorithm and PPCP without refinement functions in terms of the accuracy in detecting communities.

Appendices

Leading eigenvector method

The spectral algorithms (Newman 2006a; White and Smyth 2005; Richardson et al. 2009) use the Eigen information to partition a network into communities. The eigenvectors can be computed easily, so the community detection problem can be solved efficiently. Newman rewrite Q as the matrix and applied the spectral analysis on the modularity matrix B to design an approximated approach (Newman 2006a). To maximize Q, the Kronecker delta $\delta (g_i, g_j)$ can be defined as:

$$\begin{aligned} \delta (g_i,g_j)=\frac{s_i s_j+1}{2}, \end{aligned}$$

(6)

where $s_i = 1$ if i belongs to community one, $s_i=-\,1$ if it belongs to the other one. Note that $\delta (g_i, g_j)=1$ if i and j belong to the same community, 0 otherwise. From Eq. 6, Q can be rewritten as:

$$\begin{aligned} Q&=\frac{1}{4m}\sum _{i,j}\left( A_{i,j}-\frac{k_i k_j}{2m}\right) (s_i s_j+1) \end{aligned}$$

(7)

$$\begin{aligned}&=\frac{1}{4m}\sum _{i,j}\left( A_{i,j}-\frac{k_i k_j}{2m}\right) s_i s_j \end{aligned}$$

(8)

$$\begin{aligned}&=\frac{1}{4m}s^TBs. \end{aligned}$$

(9)

Since we have $\sum _{i, j}A_{i, j} = \sum _{i, j}k_i k_j/2m = 2m$, we can derive Eq. 8 (Newman 2006a, b). In Eq. 9, s is the index vector with the element $s_i$. So, each element in B is:

$$\begin{aligned} B_{i,j}=A_{i,j}-\frac{k_ik_j}{2m}. \end{aligned}$$

(10)

Then, we apply the spectral analysis to B. Supposing s is a linear combination of the normalized eigenvectors $u_{i}$ of B, so we have $s=\sum _{i=1}^{n}a_{i}u_{i}$ with $a_{i}=u_{i}^Ts$, and Eq. 9 can be rewritten as:

$$\begin{aligned} Q&=\frac{1}{4m}\Big (\sum _{i=1}^{n}a_{i}u_{i}^T\Big )B\Big (\sum _{j=1}^{n}a_{j}u_{j}\Big ) \end{aligned}$$

(11)

$$\begin{aligned}&=\frac{1}{4m}\Big (\sum _{i=1}^{n}a_{i}u_{i}^T\Big )\Big (\sum _{j=1}^{n}a_{j}Bu_{j}\Big ) \end{aligned}$$

(12)

$$\begin{aligned}&=\frac{1}{4m}\Big (\sum _{i=1}^{n}a_{i}u_{i}^T\Big )\Big (\sum _{j=1}^{n}a_{j}\beta _{j}u_{j}\Big ) \end{aligned}$$

(13)

$$\begin{aligned}&=\frac{1}{4m}\sum _{i}a_{i}^2\beta _{i}, \end{aligned}$$

(14)

where $\beta _{i}$ is the eigenvalue of B corresponding to eigenvector $u_{i}$. In Eq. 14, two eigenvectors $u_{i}$ and $u_{j}$ are orthogonal since B is a symmetric matrix. Assume that the eigenvalues are labeled in the descending order, e.g. $\beta _1 \ge \beta _2 \ge \cdots \ge \beta _n$. Q is maximized when $s = u_1$ with $\beta _1$. So, we have a feasible solution by choosing the leading eigenvector as the index vector.

However, $s_i$ is fractional within − 1 and 1, so the approximated solution can be derived by the following rounding approach.

$$\begin{aligned} s_i = {\left\{ \begin{array}{ll} +\,1 &{} \quad \text {if}\quad \,u_{i} \ge 0 \\ -\,1 &{} \quad \text {if}\quad \,u_{i} < 0 \end{array}\right. } \end{aligned}$$

(15)

Therefore, a network is divided into two communities by the sign of each entry of the index vector.

However, the leading eigenvector method has two implementation issues. First, the above solution divides a network into two communities, but real-world networks may consist of multiple communities. Second, we apply the leading eigenvector to design the approximation solution, but other eigenvectors are ignored. Therefore, Newman redefines Eq. 6 as (Newman 2006a):

$$\begin{aligned} \delta (g_i,g_j)=\sum _{k=1}^c S_{ik}S_{jk}, \end{aligned}$$

(16)

where S is an n-by-c index matrix with elements set as:

$$\begin{aligned} S_{ij} = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if node { i} belongs to community { j}}, \\ 0 &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(17)

Then Eq. 1 can be rewritten as:

$$\begin{aligned} Q = \text {Tr}(S^TBS). \end{aligned}$$

(18)

Vector partitioning

The leading eigenvector method only considers the first eigenvector to partition the network. In fact, other eigenvalues may make positive contribution on the modularity, so Newman transformed Eq. 18 to a general form with the first p leading eigenvalues, where $p \in [1,n]$. Thus, we have:

$$\begin{aligned} Q&=n\alpha +\sum _{k=1}^{c}\sum _{j=1}^{p}\Big [\sum _{i\in G_{k}}[r_{i}]_{_{j}}\Big ]^2 \end{aligned}$$

(19)

$$\begin{aligned}&=n\alpha +\sum _{k=1}^{c}|R_{k}|^2. \end{aligned}$$

(20)

$G_k$ is the set of vertex vectors comprising the community k and vertex vectors $r_i$ are defined as:

$$\begin{aligned} {[}r_{i}]_{_{j}}=(\sqrt{\beta _{j}-\alpha })U_{ij}, \end{aligned}$$

(21)

where $i \in \{1, 2, \ldots , n\}$, U is the Eigen matrix, and $\alpha$ is chosen to be equal to $(\sum _{i=p+1}^{n}\beta _{i}) / (n-p)$ so as to minimize the error resulted from the loss of $n - p$ eigenvectors of B (Newman 2006a).

In Eq. 20, the community vector $R_k$ are defined as:

$$\begin{aligned} R_k = \sum _{\forall i \in G_k} r_i, \end{aligned}$$

(22)

where $k=1 \ldots c$. Thus, the modularity maximization is now equivalent to find a division of vertex vectors so as to maximize the quadratic sum of norms of community vectors $R_k$.

Consider a special case of dividing a network into two communities. Since $\sum _j B_{ij} = \sum _j A_{ij} - \sum _j k_ik_j/2m = k_i-k_i = 0$ , $(1, 1, \ldots )$ always has an eigenvector of B. Moreover, eigenvectors are orthogonal since B is symmetric. Thus, the sum of the entries of all other eigenvectors must be zero:

$$\begin{aligned} \sum _{i=1}^n[u_j]_{_i} = (1, 1, \ldots ) \cdot u_j = \sqrt{n} u_1^Tu_j=0. \end{aligned}$$

(23)

From Eqs. 23, 21 implies:

$$\begin{aligned} \sum _{i=1}^n[r_i]_{_j} = \sqrt{\beta _j-\alpha }\sum _{i=1}^n U_{ij} = \sqrt{\beta _j-\alpha }\sum _{i=1}^n[u_j]_i=0, \end{aligned}$$

(24)

and we have:

$$\begin{aligned} \sum _{i=1}^n r_i = 0. \end{aligned}$$

(25)

Hence, the community vectors also sum to zero:

$$\begin{aligned} \sum _{k=1}^{c}R_k=\sum _{k=1}^c\sum _{i \in G_k}r_i = \sum _{i=1}^n r_i = 0. \end{aligned}$$

(26)

We have two communities currently and the community vectors are denoted by $R_{left}$ and $R_{right}$. There are many choices of bisection planes. For example, there are seven vertex vectors $r_1, r_2, \ldots , r_7$ in Fig. 13, and we have to choose one bisection plane. Considering three bisection planes a, b and c in Fig. 13, they all split the vertex vectors into two communities with each community vector oppositely directed and equal length. However, we can transform b and c into a without decreasing the quadratic sum of norms of community vectors. Assuming that we choose c as bisection plane where $r_7$ is one community and one of $r_1,r_2,r_3, \ldots ,r_6$ is the other community, and $R_{left}$ and $R_{right}$ are their community vectors respectively. Then removing $r_6$ from a community $R_{right}$ to $R_{left}$ where $R_{right} \cdot r_6 < 0$ produces a change in the corresponding term $|R_{right}|^2$ in Eq. 20. So, we have:

$$\begin{aligned} |R_{right} - r_6|^2 - |R_{right}|^2 = |r_6|^2 - 2R_{right} \cdot r_i > 0. \end{aligned}$$

(27)

Hence, $r_6$ can be moved to $R_{left}$, and so as $r_5$. Then, we transform c into a without decreasing the quadratic sum of norms of community vectors. Thus, the bisection plane must be a straight line going through origin such as a and partition the vertex vectors into two sets. In Fig. 13, there are seven choices of straight bisection planes. To find the best bi-partition with maximum Q, we just rotate the bisection plane and compute Q for all possible partitions. Then, we can find the best bi-partition with maximum Q over these partitions.

Fig. 13

Three different choices for the bisection plane

The meaning of eigen decomposition on modularity matrix

The vector partition applies the Eigen decomposition and selects two eigenvectors to maximize Q. In fact, the idea of the vector partition is similar to that of the Principal Component Analysis (PCA). We use the example as shown in Fig. 14 to explain how the PCA works. Given the column vector $v_i, \forall i \in \{1, 2, \ldots , n\}$, and the first principal component is denoted by $z_i = x \cdot v_i$, where x is the unit vector. The objective is to find x to maximize the variance of serial $z_i$. In Fig.  14, there are three vectors $v_1, v_2,$ and $v_3$ at Cartesian coordinate. If we choose $x = u_1$, these vectors are projected on $u_1$ as the purple nodes shown in this figure. Similarly, we will get the orange nodes if we choose $x=u_3$. In fact, the variance of the green nodes is the largest if we choose $x=u_2$. This implies that we have the largest variance if we choose the unit vector in vectors’ direction.

Fig. 14

Nodes and their projections on given vectors in 2-dimension plane

The connectivity of a social network can be represented by an adjacency matrix (Van Den Elzen et al. 2016), as shown in Fig.  15a. The black and white blocks represent the entries of 1 and 0 respectively. Based on the ground truth partition (Topchy et al. 2004), the matrix shown in Fig.  15a can be illustrated as that shown in Fig. 15b by arranging the nodes according to the community they belong to (Ruan and Zhang 2008). Thus, we have six communities and any two column vectors belonging to different communities are nearly orthogonal. If two column vectors belong to the same community, their directions are similar. Therefore, they have a hyperspace where each community represents an axis and the number of communities is the dimension of this hyperspace.

Fig. 15

Two bitmap representations for the matrix of a network

We transform the adjacency matrix to the modularity matrix as follows:

$$\begin{aligned} B_{ij} = A_{ij}-\frac{k_i k_j}{2m} \approx A_{ij}. \end{aligned}$$

(28)

The number of total edges is much more than the degree of any node in most social network. So, we have $m>> k_i$. The entry of the adjacency matrix is different from that of the modularity matrix. Thus, the difference of the angles between any pair of the column vectors in the modularity matrix will approach the angles between any pairs of the column vectors in the adjacency matrix.

Given a network with two communities and Fig. 16 is the spatial distribution of the column vectors of the modularity matrix. There are three blue column vectors $v_1, v_2,$ and $v_3$ with the first community $C_1$ and three green column vectors with the second community $C_2$. Since the column vectors which belong to different communities are almost orthogonal, we can assume that each column vector in $C_1$ is orthogonal to each column vector in $C_2$. Orange vectors a and b are first and second eigenvectors respectively. Obviously, a has a close direction with $v_1$, $v_2$ and $v_3$. Next, we will show that a node with larger degree will correspond to a vertex vector with larger norm along the direction of a in $C_1$.

Fig. 16

Nodes and their projections on given vectors in 2-dimension plane

Let B be a modularity matrix and $v_i$ is ith column vector. Then, B is:

$$\begin{aligned} B= \begin{pmatrix} B_{1,1} &{} \quad B_{1,2} \quad &{} B_{1,3} \\ B_{2,1} &{} \quad B_{2,2} &{} \quad B_{2,3} \\ B_{3,1} &{} \quad B_{3,2} &{} \quad B_{3,3} \end{pmatrix} = \begin{pmatrix} v_1&v_2&v_3 \end{pmatrix} = \begin{pmatrix} v_1&v_2&v_3 \end{pmatrix}. \end{aligned}$$

(29)

Define an unit vector $x = \begin{pmatrix}x_1&\quad x_2&\quad x_3\end{pmatrix}^T$, then the projection from $v_i$ on x is:

$$\begin{aligned} Bx = \begin{pmatrix} v_1&v_2&v_3 \end{pmatrix} \begin{pmatrix} x \end{pmatrix} = \begin{pmatrix} v_1 \cdot x \\ v_2 \cdot x \\ v_3 \cdot x \end{pmatrix}. \end{aligned}$$

(30)

Supposing $k_3> k_2 > k_1$ in $C_1$, $v_3$ has more neighbors than $k_2$ and $k_1$. The corresponding column vector has more entries in its coordinate (see Fig. 15b). Hence, we have $||v_3||> ||v_2|| > ||v_1||$ as shown in Fig.  14. To maximize the variance of serial $z_i = x \cdot v_i$, x must be chosen by the maximum norm. So, the best unit vector $x_{best}$ maximizes the difference of $z_i = x \cdot v_i$.

The variance of $z_i$ is maximized when $x_{best} = a$ where a is the first eigenvector. Here the related theoretical proof is skipped. From Eq. 30, a can be written as:

$$\begin{aligned} \lambda \begin{pmatrix} a_1\\ a_2\\ a_3 \end{pmatrix} = Bx_{best} = \begin{pmatrix} v_1 \cdot a \\ v_2 \cdot a \\ v_3 \cdot a \end{pmatrix}. \end{aligned}$$

(31)

Finally, we have:

$$\begin{aligned} \begin{pmatrix} a_1\\ a_2\\ a_3 \end{pmatrix} \propto \begin{pmatrix} v_1 \cdot a \\ v_2 \cdot a \\ v_3 \cdot a \end{pmatrix}. \end{aligned}$$

(32)

From Eq. 21, we have:

$$\begin{aligned} \begin{pmatrix} [r_1]_1 \\ [r_2]_1 \\ [r_3]_1 \end{pmatrix} = \begin{pmatrix} \sqrt{\beta _1 - \alpha }a_1 \\ \sqrt{\beta _1 - \alpha }a_2 \\ \sqrt{\beta _1 - \alpha }a_3 \end{pmatrix} \propto \begin{pmatrix} v_{1} \cdot a \\ v_{2} \cdot a \\ v_{3} \cdot a \end{pmatrix}. \end{aligned}$$

(33)

Hence, in $C_1$, $r_3$ which corresponds to the node with the largest degree has the largest norm along a over other vertex vectors in the same community.

Since a must be chosen as close to $v_3$ as possible, $v_3 \cdot a$ is the greatest one among other entries. From Eq. 33, we have:

$$\begin{aligned} {[}r_3]_1> [r_2]_1 > [r_1]_1. \end{aligned}$$

(34)

Hence, if a is chosen as the new x-axis, $r_3$ has the largest norm along direction of a among $r_1$ and $r_2$ in $C_1$. On the other hand, $r_4$, $r_5$ and $r_6$ will have small norm along the direction of a since $v_4$, $v_5$ and $v_6$ are almost orthogonal to a. By the same way, $r_5$ has the largest norm as b is the new y-axis. Therefore, plotting $r_i$, $i \in \{1, 2, \ldots , 7\}$ at the polar coordinate system, any two vertex vectors belonging to different communities will be separated by an angle as shown in Fig.  17.

Fig. 17

Six vertex vectors at polar coordinate system

Spectral clustering and ratio-cut

The high-dimension data consists of many attributes, but critical attributes which can be used to partition the network may be few. If we can find out the critical attributes, we can simplify the data and analyze the property easily. The spectral clustering is designed based on finding the critical attributes. First, the data are represented as a similarity matrix L where $L_{ij}$ indicates the similarity between node i and node j. Then, we can capture the eigenvectors based on the similarity matrix. The eigenvector with large eigenvalue provides important information about the data. This idea is similar to the PCA.

Chen et al. propose the ratio-cut to partition the network (Chen et al. 2014). Supposed A is the adjacency matrix where $A_{ij}$ is an edge between node i and node j. The corresponding degree matrix is denoted by D, which is a diagonal matrix and $A_{ii}$ is the degree of i. Define Laplacian matrix as $L = D - A$. A ratio-cut partition for a network $G=(V, E)$ is defined as a partition of V into two disjoint sets U and W with minimum cost $c = (Cut(U, W)) / (|U||W|)$. In Pothen et al. (1990), Pothen et al. proved that the second eigenvalue $\lambda$ yields a lower bound on the optimal cost of ratio-cut partition with $c \ge \lambda / n$. Thus, we can partition a network into two communities according to the sign of the entry of this eigenvector.

However, |U||W| in c implies that the ratio-cut is appropriate for balanced divisions. For example, consider a network merged by two communities with different sizes. We will get two communities with similar size by the ratio-cut. Hence, the ratio-cut performs better in balanced networks than in unbalanced cases.