Abstract
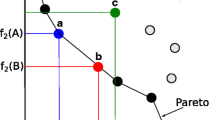
The paper presents a constraint-handling approach for multi-objective optimization. The general idea is shown as follow: Firstly, the population was classified into two groups: feasible population and infeasible population. Secondly, feasible population was classified into Pareto population and un-Pareto population. Thirdly, the Pareto population was defied with k-average classify approach into colony Pareto population and in-colony Pareto population. Last, R-fitness was given to each population. Simulation results show that the algorithm not only improves the rate of convergence but also can find feasible Pareto solutions distribute abroad and even.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Schaffer JD (1985) Multiple objective optimization with vector evaluated genetic algorithms. In: Grefenstette J (ed) Proceedings of an international conference on genetic algorithms and their applications
Horn J, Nafpliotis N, Goldberg DE (1994) A niched Pareto genetic algorithm for multiobjective optimization. In: Proceedings of the first IEEE conference on evolutionary computation. Piscataway, pp 82–87
Fonseca CM, Fleming PJ (1993) Genetic algorithms for multiobjective optimization: formulation, discussion and generalization. In: Proceeding of the fifth international conference on genetic algorithms. Morgan Kauffman, San Francisco
Deb K, Agrawal S, Pratap A, Meyarivan T (200) A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II, KanGAL report No. 200001
Zitzler E, Deb K, Thiele L (2000) Comparison of multiobjective evolutionary algorithms: empirical results.Evol Comput 8(2):125--147
Jimenez F, Verdegay J (1999) Evolutionary techniques for constrained optimization problems. In: 7th European congress on intelligent techniques and soft computing (EUFIT’99), Springer, Aachen, Germany
Wang Y, Liu L (2005) Constrained multi-objective optimization evolutionary algorithm. J Tsinghua Univ (Nat Sci Ed) 45(1):103–106
Wang X, Cao L (2002) Genetic algorithm theory, application and software implementation. Xi’an Jiao Tong University press, Xi’an
Wen X, Zhou L, Wang D (2000) MATLAB Neural network application design. Science press, Beijing
Wang L (2001) Intelligent optimization algorithm and its application. Qinghua University press, Beijing
Xing W, Xie J (2000) Modern optimization method. Qinghua University press, Beijing
Anderson R, Lew D (2003) Evaluating predictive models of species distributions: criteria for selecting optimal models. Ecol Model 162(3):211–232
Acknowledgments
This Project supported by College youth talents foundation of Anhui Province (2012SQRL259) and Anhui University Of Science And Technology university scientific research projects.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Zhang, Ll., Xu, F., Hu, J. (2013). Multi-Objective Genetic Algorithm with Complex Constraints Based on Colony Classify. In: Yin, Z., Pan, L., Fang, X. (eds) Proceedings of The Eighth International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA), 2013. Advances in Intelligent Systems and Computing, vol 212. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-37502-6_20
Download citation
DOI: https://doi.org/10.1007/978-3-642-37502-6_20
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-37501-9
Online ISBN: 978-3-642-37502-6
eBook Packages: EngineeringEngineering (R0)