Abstract
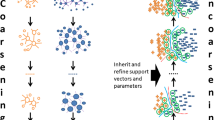
In many classification applications, Support Vector Machines (SVMs) have proven to be highly performing and easy to handle classifiers with very good generalization abilities. However, one drawback of the SVM is its rather high classification complexity which scales linearly with the number of Support Vectors (SVs). This is due to the fact that for the classification of one sample, the kernel function has to be evaluated for all SVs. To speed up classification, different approaches have been published, most which of try to reduce the number of SVs. In our work, which is especially suitable for very large datasets, we follow a different approach: as we showed in (Zapien et al. 2006), it is effectively possible to approximate large SVM problems by decomposing the original problem into linear subproblems, where each subproblem can be evaluated in Ω(1). This approach is especially successful, when the assumption holds that a large classification problem can be split into mainly easy and only a few hard subproblems. On standard benchmark datasets, this approach achieved great speedups while suffering only sightly in terms of classification accuracy and generalization ability. In this contribution, we extend the methods introduced in (Zapien et al. 2006) using not only linear, but also non-linear subproblems for the decomposition of the original problem which further increases the classification performance with only a little loss in terms of speed. An implementation of our method is available in (Ronneberger and et al.) Due to page limitations, we had to move some of theoretic details (e.g. proofs) and extensive experimental results to a technical report (Zapien et al. 2007).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
V. VAPNIK (1995): The Nature of Statistical Learning Theory, New York: Springer Verlag.
Y. LEE and O. MANGASARIAN (2001): RSVM: Reduced Support Vector Machines, Pro-ceedings of the first SIAM International Conference onData Mining, 2001 SIAM Inter-national Conference, Chicago, Philadelphia.
H. LEI and V. GOVINDARAJU (2005): Speeding Up Multi-class SVM Evaluation by PCA andFeature Selection, Proceedings of the Workshop on Feature Selection for DataMin-ing: Interfacing Machine Learning and Statistics, 2005 SIAM Workshop.
C. BURGES and B. SCHOELKOPF (1997): Improving Speed and Accuracy of Support Vector Learning Machines, Advances in Neural Information Processing Systems9, MIT Press, MA, pp 375-381.
K. P. BENNETT and E. J. BREDENSTEINER (2000): Duality and Geometry in SVM Clas-sifiers, Proc. 17th International Conf. on Machine Learning, pp 57-64.
C. HSU and C. LIN (2001): A Comparison of Methods for Multi-Class Support Vector Ma-chines, Technical report, Department of Computer Science and Information Engineering, National Taiwan University, Taipei, Taiwan.
T. K. HO AND E. M. KLEINBERG (1996): Building projectable classifiers of arbitrary com-plexity, Proceedings of the 13th International Conference onPattern Recognition, pp 880-885, Vienna, Austria.
B. SCHOELKOPF and A. SMOLA (2002): Learning with Kernels, The MIT Press, Cam-bridge,MA, USA.
S. KEERTHI and S. SHEVADE and C. Bhattacharyya and K. Murthy (1999): Improvements to Platt’s SMO Algorithm for SVM Classifier Design, Technical report, Dept. ofCSA, Banglore, India.
P. CARBONETTO: Face data base, http://www.cs.ubc.ca/pcarbo/, University of British Columbia Computer Science Deptartment.
J. J. HULL (1994): A database for handwritten text recognition research, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 16, No 5, pp 550-554.
K. ZAPIEN, J. FEHR and H. BURKHARDT (2006): Fast Support Vector Machine Classifi-cation using linear SVMs, in Proceedings: ICPR, pp. 366- 369 ,Hong Kong 2006.
O. RONNEBERGER and et al.: SVM template library, University of Freiburg, Depart-ment of Computer Science, Chair of Pattern Recognition and Image Processing, http://lmb.informatik.uni-freiburg.de/lmbsoft/libsvmtl/index.en.html
K. ZAPIEN, J. FEHR and H. BURKHARDT (2007): Fast Support Vector Machine Classi-fication of very large Datasets, Technical Report 2/2007, University of Freiburg, De-partment of Computer Science, Chair of Pattern Recognition and Image Processing. http://lmb.informatik.uni-freiburg.de/people/fehr/svm_tree.pdf
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Fehr, J., Arreola, K.Z., Burkhardt, H. (2008). Fast Support Vector Machine Classification of Very Large Datasets. In: Preisach, C., Burkhardt, H., Schmidt-Thieme, L., Decker, R. (eds) Data Analysis, Machine Learning and Applications. Studies in Classification, Data Analysis, and Knowledge Organization. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-78246-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-540-78246-9_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-78239-1
Online ISBN: 978-3-540-78246-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)