Abstract
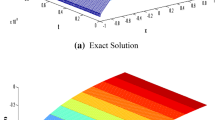
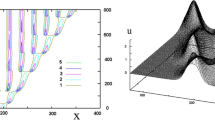
Bridging the gap between clinical applications and mathematical models is one of the new challenges of medical image analysis. In this paper, we propose an efficient and accurate algorithm to solve anisotropic Eikonal equations, in order to link biological models using reaction-diffusion equations to clinical observations, such as medical images. The example application we use to demonstrate our methodology is tumor growth modeling. We simulate the motion of the tumor front visible in images and give preliminary results by solving the derived anisotropic Eikonal equation with the recursive fast marching algorithm.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Aronson, D., Weinberger, H.: Multidimensional nonlinear diffusion arising in population genetics. Advances in Mathematics 30 (1978)
Ebert, U.: W.S.: Front propagation into unstable states: universal algebraic convergence towards uniformly translating pulled fronts. Physica D: Nonlinear Phenomena 146 (2000)
Tovi, M.: Mr imaging in cerebral gliomas analysis of tumour tissue components. Acta Radiol. Suppl. (1993)
Sethian, J., Vladimirsky, A.: Ordered upwind methods for static hamilton-jacobi equations: theory and algorithms. SIAM J. Numer. Anal. 41 (2003)
Kao, C., Osher, S., Tsai, Y.: Fast sweeping methods for static hamilton-jacobi equations. SIAM J. Numer. Anal. 42 (2005)
Qian, J., Zhang, Y., Zhao, H.: A fast sweeping method for static convex hamilton-jacobi equations. UCLA Comp. and App. Math. Reports, 06-37 (2006)
Kevorkian, J.: Partial differential equations: Analytical solution techniques. Springer, Heidelberg (2000)
Sethian, J.: Level set methods and fast marching methods: Evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science. Cambridge University Press, Cambridge (1999)
Qian, J., Symes, W.: Paraxial eikonal solvers for anisotropic quasi-p travel times. J. Comp. Physics, 173 (2001)
Keener, J., Sneyd, J.: Mathematical physiology. Springer, Heidelberg (1998)
Murray, J.: Mathematical Biology. Springer, Heidelberg (2002)
Maini, P., McElwain, D., Leavesley, D.: Traveling wave model to interpret a wound-healing cell migration assay for human peritoneal mesothelial cells. Tissue Eng. 10 (2004)
Bramson, M.: Convergence of solutions of the kolmogoroff equations to traveling waves. Mem. Am. Math. Soc (1983)
Cristini, V., Lowengrub, J., Nie, Q.: Nonlinear simulation of tumor growth. Journal of Math. Biol. 46 (2003)
Swanson, K., Alvord, E., Murray, J.: Virtual brain tumours (gliomas) enhance the reality of medical imaging and highlight inadequacies of current therapy. British Journal of Cancer, 86 (2002)
Clatz, O., Sermesant, M., Bondiau, P., Delingette, H., Warfield, S., Malandain, G., Ayache, N.: Realistic simulation of the 3d growth of brain tumors in mr images coupling diffusion with biomechanical deformation. IEEE T.M.I. 24(10) (2005)
Giese, A., Kluwe, L., Laube, B., Meissner, H., Berens, M., Westphal, M.: Migration of human glioma cells on myelin. Neurosurgery, 38(4) (1996)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2007 Springer Berlin Heidelberg
About this paper
Cite this paper
Konukoglu, E., Sermesant, M., Clatz, O., Peyrat, JM., Delingette, H., Ayache, N. (2007). A Recursive Anisotropic Fast Marching Approach to Reaction Diffusion Equation: Application to Tumor Growth Modeling. In: Karssemeijer, N., Lelieveldt, B. (eds) Information Processing in Medical Imaging. IPMI 2007. Lecture Notes in Computer Science, vol 4584. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-73273-0_57
Download citation
DOI: https://doi.org/10.1007/978-3-540-73273-0_57
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-73272-3
Online ISBN: 978-3-540-73273-0
eBook Packages: Computer ScienceComputer Science (R0)