Keywords

1 Introduction

The goal of video cosegmentation is to jointly extract the common foreground regions and/or objects from a set of videos. The video cosegmentation can be considered weakly supervised [7], since the presence of common foreground regions and/or objects in multiple videos provides some indication that is not available to the unsupervised problem of segmentation for a single video. That additional information may help, but it may not be enough to reduce the ambiguity in video cosegmentation of general content, due to the presence of multiple foreground regions and/or objects with low contrast to the background.

In this paper, we present a novel approach for video cosegmentation that uses graph-based hierarchical clustering as its basic component. Our graph-based Hierarchical Video Cosegmentation method (HVC) presents two main technical contributions. The former is the adoption of a simple graph-based hierarchical clustering method as key component of the framework which respects two important principles of multi-scale set analysis, i.e., causality and location principles [9]. Therefore, it is able to produce a set of video segments that are more homogeneous and whose borders are better defined using simple features to calculate dissimilarity measure between neighboring pixels and voxels (instead of several and expensive features which are very common in other approaches found in the literature). The second one is the removal of the need for parameter tuning and for the computation of a segmentation at finer levels, since it is possible to compute any level without computing the previous ones.

The few existing methods for video cosegmentation are all based on low-level features. In [11], the authors separated foreground and background regions through an iterative process based on feature matching among video frame regions and spatio-temporal tubes. The video cosegmentation method presented in [4] can extract multiple foreground objects by learning a global appearance model that connects segments of the same class. It also uses the Bag-of-Words (BoW) representation for multi-class video cosegmentation. While BoW provides more discriminative ability than basic color and texture features, they may be susceptible to appearance variations of foreground objects in different videos, due to factors such as pose change. In [15], the authors proposed a method which employs the object proposal [5] as the basic element, and uses the regulated maximum weight clique method to select the corresponding nodes for video multi-class segmentation. Finally, in [7], the authors proposed a multi-state selection graph in which a node representing a video frame can take multiple labels that correspond to different objects (also based on object proposal [5]). In addition, they used an indicator matrix to handle foreground objects that are missing in some videos, and they also presented an iterative procedure to optimize an energy function along with that indicator matrix.

The paper is organized as follows. Section 2 presents concepts about graph-based hierarchical clustering used in this work. While Sect. 3 describes our method to cope with video cosegmentation problem, Sect. 4 presents experimental results of our approach together with a comparative analysis with others methods from the literature. Finally, we draw some conclusions in Sect. 5.

2 Graph-Based Hierarchical Clustering

Following the seminal ideas proposed in [10], a hierarchy of partitions based on observation scales can be computed using a criterion for region-merging popularized by [6]. Moreover, it satisfies two important principles of multi-scale set analysis, i.e., causality and location principles [9]. Namely, and in contrast with the approach presented in [6], the number of regions is decreasing when the scale parameter increases, and the contours do not move from one scale to another.

Thanks to that, one can compute the hierarchical observation scales for any graph, in which the adjacent graph regions are evaluated depending on the order of their merging in the fusion tree, i.e., the order of merging between connected components on the minimum spanning tree (MST) of the original graph. Actually, one does not need to produce explicitly a hierarchy of partitions, since a weight map with observation scales can be used to infer the desired hierarchy, e.g., by removing those edges whose weight is greater than a desired scale value. This map is a new edge-weighted tree created from MST in which each edge weight corresponds to the scale from which two adjacent regions connected by this edge are correctly merged, i.e., there are no other sub-regions of these regions that might be merged before these two.

Following [10], for computing the weight map of observation scales, we consider the criterion for region-merging proposed in [6] which measures the evidence for a boundary between two regions by comparing two quantities: one based on intensity differences across the boundary, and the other based on intensity differences between neighboring pixels within each region. More precisely, in order to know whether two regions must be merged, two measures are considered. The internal difference \( Int ({X})\) of a region \(X\) is the highest edge weight among all the edges linking two vertices of \(X\) in MST. The difference \( Diff ({X},{Y})\) between two neighboring regions \(X\) and \(Y\) is the smallest edge weight among all the edges that link \(X\) to \(Y\). Then, two regions \(X\) and \(Y\) are merged when:

$$\begin{aligned} Diff ({X},{Y})\le \min \left\{ Int ({X})+\frac{\lambda }{|X|}, Int ({Y})+\frac{\lambda }{|Y|}\right\} \end{aligned}$$
(1)

in which \(\lambda \) is a parameter used to prevent the merging of large regions, i.e., larger \(\lambda \) forces smaller regions to be merged.

The merging criterion defined by Eq. (1) depends on the scale \(\lambda \) at which the regions \(X\) and \(Y\) are observed. More precisely, let us consider the (observation) scale \(S_{Y}({X})\) of \(X\) relative to \(Y\) as a measure based on the difference between \(X\) and \(Y\), on the internal difference of \(X\) and on the size of \(X\):

$$\begin{aligned} S_{Y}({X})=( Diff ({X},{Y})- Int ({X}))\times ~|X|. \end{aligned}$$
(2)

Then, the scale \(S(X,Y)\) is simply defined as:

$$\begin{aligned} S(X,Y)=\max (S_{Y}({X}),S_{X}({Y})). \end{aligned}$$
(3)

Thanks to this notion of a scale, Eq. (1) can be written as:

$$\begin{aligned} \lambda \ge S(X,Y). \end{aligned}$$
(4)

The core of [10] is the identification of the smallest scale value that can be used to merge the largest region to another one while guaranteeing that the internal differences of these merged regions are greater than the value calculated for smaller scales. The hierarchization of this principle has been successfully applied to several tasks: image segmentation [10], video segmentation [12,13,14], and video summarization [3]. In next section, we present our proposal to extend its application to the video cosegmentation problem.

3 Proposed Method

In this work, video cosegmentation problem is transformed into a graph-based clustering task in which a cluster (or connected component of the graph), computed from a graph partition, represents a set of similar supervoxels belonging to the analyzed videos. In order to do that, our proposed method, named HVC, is divided in two main parts: (i) supervoxel generation; and (ii) supervoxel correlation. The former explores only intra-video similarities, while the latter seeks to determine relationships between supervoxels belonging to the same video (intra-video similarity) or to distinct videos (inter-video similarity).

Fig. 1.
figure 1

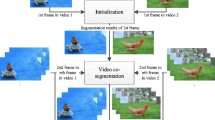
Outline of our method: each video is transformed into a video graph (step 1); a hierarchy is computed from each video graph (step 2); the identification of video segments (supervoxels) is made from each hierarchy (step 3); each set of supervoxels is described (step 4) and a single supervoxel graph is generated (step 5); another hierarchy is computed from supervoxel graph (step 6); a partition of supervoxel graph is obtained (step 7); and, finally, the identification of connected components is made (step 8).

Full size image

Figure 1 illustrates the steps of HVC method. First, each video is transformed into a video graph (step 1). Then, to explore the intra-video similarity, a hierarchy is computed from each video graph (step 2) and the identification of video segments (supervoxels) is made from each hierarchy (step 3). For each video, its set of supervoxels is described (step 4) and a single supervoxel graph is generated (step 5) containing all supervoxels from every video, in order to analyze both intra and inter-video similarities. Again, another hierarchy is computed from supervoxel graph (step 6) and a partition of supervoxel graph is obtained (step 7). And, finally, the identification of connected components (i.e., “cosegments”) is made (step 8).

An example of HVC results can be seen in Fig. 2 for both parts: supervoxels generation and correlation. The first part – supervoxel generation (steps 1 to 3) – adopts a hierarchical video segmentation (very similar to HOScale method proposed in [13, 14]) that helps producing supervoxels that are more homogeneous and whose borders are better defined (HOScale exhibits high values for 3D segmentation accuracy and boundary recall and a low undersegmentation error [13, 14]). The second part – supervoxels correlation (steps 4 to 8) – also utilizes a graph-based hierarchical clustering method based on [10], but applied to a complete graph generated from video segments obtained before. This removes the need for parameter tuning, resulting in a method that is not dependent on the hierarchical level, and consequently, making possible to compute any level without computing the previous ones [10]. Moreover, this is done using simple features to calculate dissimilarity measure between neighboring pixels and voxels (more details are given in Sect. 4).

Fig. 2.
figure 2

HVC results for two videos with the same pair of vases. First row presents some samples of the original video frames. Video segments are illustrated at the second line (i.e., pixels with the same color belong to the same supervoxel); and, finally, cosegmentation results are presented at the third line (i.e., the same color is adopted to present pixels from common regions between videos).

Full size image

The method HVC depends on: (i) the dissimilarity measure used in video graphs; (ii) the minimum size of a video segments (\(min_{vs}\)); (iii) the number of those segments (\(n_{vs}\)) per video; (iv) the dissimilarity measure used in supervoxel graph; (v) the minimum size of connected component (\(min_{cc}\)) for eliminating outliers during supervoxel clustering step; and (vi) the number of connected components (\(n_{cc}\)) used for obtaining a video cosegmentation.

4 Experiments

In order to evaluate our proposed method HVC, we used two well-known datasets: (i) ObMiC [7, 8]; and (ii) MOViCS [4]. ObMiC dataset [7, 8] is composed of four sets of video pairs each with two foreground objects in common, and the ground truth is manually labeled for each frame. MOViCS dataset [4] contains four video sets with 11 videos in total, and five frames of each video are labeled with ground truth at the pixel level.

During supervoxel generation, video graphs are the ones induced by the 26-adjacency pixel relationship, in which edge weights are calculated by a simple color gradient computed using the Euclidean distance in Lab color space, and we set \(n_{vs}\) to 100, 200, 300, 400, and 500. The supervoxel graph is generated as a complete graph, combining every possible number of video segments. In order to improve the strength of the relationship between supervoxels related to objects (or foreground regions) belonging to the same video (i.e., intra-video similarity) an objectness measure (i.e., a value which reflects how likely an image window covers an object of any category [1]) was used. The average value of objectness for every supervoxel was computed from the objectness values from its pixels. Following [1], to calculate the objectness value for a pixel p, the objectness measure was applied to 1,000 random windows for each video frame and the measure obtained for each window is added if it contains the pixel p. Actually, we adopted a normalized version of that objectness measure per pixel, called heatmap, in which pixels values are rescaled to [0, 1] and used to produced a pseudo-colored image where areas with high probability of containing an object are shown in red, while dark blue indicates the absence of any object (see Fig. 3). Finally, \(n_{cc}\) is set to 5%, 10%, 15%, 20%, and 25% of the total number of nodes of the supervoxel graph.

Fig. 3.
figure 3

Examples of heatmaps generated from objectness measure. (Color figure online)

Full size image

We have compared our method HVC against two cosegmentation methods from the literatureFootnote 1: (i) Regulated Maximum Weight Cliques (RMWC) [15]; and (ii) Multi-state Selection Graph (MSG) [7]. Differently from [7], the used MSG implementation does not have any post-processing, since the available code does not have any pixel-level refinement step in it. This allows a much fair comparison among different approaches because we can focus on the actual results generated by the cosegmentation methods (instead of considering improvements from post-processing steps that may be applied to the results of any approach).

To assess the quality of obtained cosegmentation results, we adopted two metrics (similar to [7]) to evaluate accuracy and error rate: (i) the average Intersection-over-Union (IoU); and (ii) the average per-frame pixel error (pFPE), respectively. We present IoU and pFPE scores that are optimal considering a constant scale parameter for the whole database (ODS) and a scale parameter varying for each video (OVS) (analogously to [2]). Thus, HVC\(_D\) and HVC\(_V\) stand for the results of HVC with a constant scale parameter for the whole database (ODS) and a scale parameter varying for each video (OVS), respectively.

Table 1 presents accuracy results on both datasets. The method HVC\(_V\) outperforms on average RMWC for both datasets (for MOViCS dataset, the difference in average accuracy is only 1%). The performance of MSG is very poor on MOViCS dataset, but it has presented an average accuracy 5% greater than HVC\(_V\) on ObMiC dataset. As one can see in Fig. 4, good accuracy results are related to low values of pFPE. Actually, MSG method presented the lowest pFPE value on average for ObMiC dataset and the highest one for MOViCS dataset, which could explain its good results for the former and poor performance for the latter (e.g., see the results for video class Tiger on MOViCS dataset).

Table 1. Accuracy results for different methods on ObMiC and MOViCS datasets.
Full size table
Fig. 4.
figure 4

Accuracy and error on the ObMiC and MOViCS dataset for different methods.

Full size image

In order to assess qualitatively the obtained cosegmentation results, some examples for different approaches on ObMiC dataset are shown in Fig. 5. Results are presented for two videos from each class, along with the original video frames and the expected results (i.e., ground truth). For video class Dog, RMWC results were very poor, while MSG and HVC produced similar results (with a little advantage for MSG method). The same pattern can be observed for video class Skating (but in this case MSG method was even better). For video class Monster, both RMWC and MSG methods have failed to identify one of the expected objects. Moreover, MSG method has assigned an instance of those objects from the first video to a different one in the second video. Finally, for video class Person, HVC was able to identify both persons (without the heads), while RMWC and MSG have continued failing in identifying one of them. This is similar to what happened for class Monster, except that in this case an object instance from the first video was divided and assigned to distinct parts of the same object (by RMWC) or to segments belonging to two different objects (by MSG).

Fig. 5.
figure 5

Cosegmentation results on ObMiC dataset. From top to bottom: original video frames, ground truth, RMWC [15], MSG [7], and our proposed method HVC.

Full size image

Similarly, some results produced by different approaches on MOViCS dataset are shown in Fig. 6. As before, results are presented for each class, along with the original video frames and the expected results (i.e., ground truth), but some classes have more than two results since they have more videos (03 for class Tiger and 04 for class Lion). For classes Chicken and Lion, RMWC has shown the best results followed closely by HVC method, while MSG results were very poor (it has divided some objects and has also considered some similar object instances as distinct). Finally, for classes Giraffe and Tiger, the opposite occurred: HVC presented best results followed by RMWC (while MSG showed some improvement only for class Giraffe).

Fig. 6.
figure 6

Cosegmentation results on MOViCS dataset. From top to bottom: original video frames, ground truth, RMWC [15], MSG [7], and our proposed method HVC.

Full size image

It is worth to mention that, for the class Dog, the proposed method HVC was not able to relate any segment of the second video to anyone belonging to the first one. This problem probably occurs due to the low differences between color averages of regions belonging to the same video. The same problem has also happened with RMWC (see the third video of the class Tiger).

Finally, HVC method is able to obtain very good results on both datasets using only a small amount of time. Table 2 presents total and average (per frame) time spent for tested methods on both datasets. For ObMiC dataset, HVC spent only 45.5% and 32.2% of the time spent on average by RMWC and MSG, respectively; while it spent on average 26.6% and 44.5% of the time spent by RMVC and MSG, respectively, for MOViCS dataset. The method MSG outperforms HVC on ObMiC dataset, but since it uses a great number of (computational expensive) features it took 211% more time to obtain the its results.

Table 2. Time spent for different methods on ObMiC and MOViCS datasets.
Full size table

5 Conclusion

In this paper, we present a novel approach for video cosegmentation that uses graph-based hierarchical clustering as its basic component. Our method HVC presents two main technical contributions. The former is the adoption of a simple graph-based hierarchical clustering method as key component of the framework which respects two important principles of multi-scale set analysis, i.e., causality and location principles [9]. Therefore, it is able to produce a set of video segments that are more homogeneous and whose borders are better defined using simple features to calculate dissimilarity measure between neighboring pixels and voxels (instead of several and expensive features which are very common in other approaches found in the literature). The second one is the removal of the need for parameter tuning and for the computation of a segmentation at finer levels, since it is possible to compute any level without computing the previous ones.

In this work, video cosegmentation problem is transformed into a graph-based clustering task in which a cluster (or connected component of the graph), computed from a graph partition, represents a set of similar supervoxels belonging to the analyzed videos. Our proposed method HVC is divided in two main parts: (i) supervoxel generation; and (ii) supervoxel correlation. The former explores only intra-video similarities, while the latter seeks to determine relationships between supervoxels belonging to the same video (intra-video similarity) or to distinct videos (inter-video similarity). Moreover, HVC uses simple features to calculate dissimilarity measure between neighboring pixels and voxels.

Experimental results provide quantitative and qualitative comparison involving new approach and other methods from the literature on two well known datasets, showing that HVC is a competitive approach. Concerning quality measures, HVC outperforms on average both tested methods for one dataset; and it presents on average an accuracy of 5% less than the best method for the other dataset. In spite of that, HVC method represents an attractive approach which is able to produce good quality results without being too computational expensive. When compared to the other methods, it took less than 50% of the time spent by any other approach.

In order to improve and better understand our results, further works involve inclusion of new features and automatic identification of the number of connected components; and also the application to another datasets.