Palm Trees Detection from High Spatial Resolution Satellite Imagery Using a New Contextual Classification Method with Constraints

Abstract

Palm groves are one of the most characteristic agro-ecosystems of Morocco. Therefore, conservation and monitoring have become a primary objective, not just from an environmental and landscaping point of view but also from the socio-economic. In this context, remote sensing presents an effective tool to map palm groves, to count palm trees and to detect their possible diseases.

The present study attempts to map palm trees from very high resolution WorldView 2 (WV 2) imagery, using a new supervised contextual classification method based on Markov Random Fields and palm trees shadow orientation. A combined layer of pan-sharpened multi-spectral (MS) bands and eight mean texture measures based Gray Level Co-occurrence Matrices (GLCM) were used as input variables. Total accuracy of 83.4 % palm trees detection was achieved. Using a decision criterion based on palm trees: shape, shadow orientation and the distance, the total accuracy of palm trees detection reached 88.1 %.

1 Introduction

Palm groves are one of the most characteristic agro-ecosystems of Morocco, not only for their natural and scenic value, but also because over hundreds of years, they have created a favorable environment that man has used to cultivate, taking advantage of the microclimate and protection offered by the palm trees in this arid environment. Therefore, conservation and monitoring have become a primary objective, not just from an environmental and landscaping point of view but also from the socio-economic.

In this sense, remote sensing presents an effective tool to map palm groves, to count palm trees, and to detect their possible diseases. To date, no specific document touching the use of remote sensing to map date palms in Morocco has been published. However, some authors have demonstrated the potential of satellite images in other parts of the world not just to identify palm trees, but also to detect the symptoms of diseases. In [1] the authors have mapped the date palm trees in urban and agricultural areas in Kuwait. They have used panchromatic and multispectral sensor of Quickbird with a resolution of 60 cm. Although the results show a level of accuracy 96 %, it should be noted that their study is limited to areas where there are palm trees of 3 m or more in diameter, and most importantly, the distance between them should be greater than 3–8 m. Similar studies were conducted in Malaysia, and in this case the goal was to detect and count the palm oil plantations [2]. The authors used data from an airborne senor with a spatial resolution of 1 m and 20 spectral bands. They scored higher levels of accuracy to 90 %, but always there were no palm trees with an overlap. In [3] although it is not specifically devoted to the classification of palm trees, the authors made a comparative analysis between IKONOS and WorldView-2 imagery to map different species of trees in an urban environment. We note in their results for palm category (all existing species in the studied area), the success rate was only 40 %. They tried to reason with the fact that the diameters of palm trees were small (< 3 m) and the presence of a mixing effect with surfaces below and around the palm trees. We could cite further studies, all with good results but provided that the palm trees are large and separated by a distance from each other.

The process of the classification can be performed in several ways, e.g., supervised or unsupervised, parametric or nonparametric, contextual or non-contextual. In this paper, we focus on the application of a supervised contextual classification method using a Markov Random Fields (MRF). In image processing the fundamental idea of the MRF is to introduce contextual relations on a local neighborhood, with MRF, pixels are not considered any more independently but in their globality. Thus, besides spectral values for each pixel, information from its neighboring pixels is also evaluated. In this regard, we have used the Iterated Conditional Mode (ICM) algorithm [4, 5] with a parameter of temperature inspired from the simulated annealing algorithm [6]. Basically, this parametric method models the prior distribution of the image as a locally dependent Markov random field, for which the maximum a posteriori estimate is approximated iteratively.

This paper is organized as follows: in Sect. 2, we present an overview of the processing workflow. In Sect. 3, the developed ICM classification algorithm with constraints is described. Then in Sect. 4, the preliminary results are given and the post-classification decision criterion is used to improve results. Finally, conclusions are given in Sect. 5.

2 The Proposed Workflow

Due to the complexity of the scenes and of the several factors limiting digital palm trees detection, our conceptual workflow incorporates three blocks. The first block is devoted to the pre-processing, the second is related to the classification process and the third block to identify palm trees using shape and shadow direction information. The classified image is compared with the validation samples to determine the level of accuracy of the resulting classification. The workflow outlining steps of our methodology is shown in Fig. 1.

Fig. 1.

Processing flow chart of the palm trees mapping.

3 The Classification Developed Method

3.1 The Contextual Image Model

3.1.1 Markov Random Fields in Imagery

We are given an image MxN defined on $\varOmega =\left\{ s=(i,j);1\le i\le M,1\le j\le N\right\}$ with value in E, thus, an element $x_s$ of E is a matrix $x=(x_s ,s\in \varOmega )$ where $x_s$ is for example the gray scale associated to the site s.

To the family $V=\left\{ V(s),s\in \varOmega \right\}$ is associated a class of the distribution probability, called Markov field and characterized by the following property:

$$\begin{aligned} {\left\{ \begin{array}{ll} P(x_s)\succ 0 \text {, for any configuration}\,x_s \\ P(x_s|x_r,r\in \varOmega -\{s\})=P(x_s|x_r ,r\in V(s)-\{s\}). \end{array}\right. } \end{aligned}$$

(1)

The probability of a pixel $x_{s}$ conditional to all the others is equal to the conditional probability of $x_{s}$ knowing the pixels of its local neighborhood V(s). The value of the other sites r is supposed known $r\in \varOmega -\left\{ s\right\}$. In the context of land cover classification, this property implies that the same land cover class is more likely to occur in connected regions than isolated pixels.

With a given neighborhood system corresponds a set of cliques. A clique is a set of points of the lattice that are mutually neighboring. The order of a clique is the number of sites which compose it. Two pixels belong to a clique if they are mutually neighboring each other. So, U(x) which can be decomposed on all the cliques of the image, and expressed as a sum of associated potentials to these cliques:

$$\begin{aligned} U(x)=\sum _{c\subset C}V_{c} (x). \end{aligned}$$

(2)

The theorem of Hammersley-Clifford [5] makes it possible to characterize the MRFs in overall terms from the expression of the a priori probability of a configuration of the classes$P\left( X=x\right)$. It allows to establish a correspondence between a Markov field and a Gibbs field when no realization of X has a null probability. It shows that a definite random field on a network is a Markovian field if and only if its distribution of the a priori probability P(x) is a Gibbs distribution, defined by:

$$\begin{aligned} P\left( x\right) =\frac{1}{Z} e^{-U\left( x\right) } , \end{aligned}$$

(3)

where Z is a normalizing constant.

3.1.2 The Estimation Criteria in MRF

There are several criteria for estimating the variables of interest x. The one which is applied in the developed method is the estimator of the Maximisation of the a posteriori (MAP). So, the best estimation is the most probable given the observed realization y and which amounts to minimize the energy U(x).

In the case of MAP, there exist several methods of researching its solution: deterministic or stochastic. In our work we have opted for a deterministic method, which is the Iterated Conditional Mode method (ICM), because our goal is to process images of large sizes and with this method the convergence is guaranteed with a reasonable time of execution.

3.1.3 Minimization of the Posterior Energy by the ICM

Proposed by Besag [4], by assigning to each site s the class that maximizes the conditional probability to the observation in s and therefore minimizes the function of energy.

Let $Y=\left\{ Y_{s} =y_{s} ;s\in \varOmega \right\}$ and $X=\left\{ X_{s} =x_{s} ;s\in \varOmega \right\}$. Each pixel configuration $x_{s }$ denotes one land cover class. Hence, $x_{s} \in \left\{ 1,...,L\right\}$. A simple way to see this method is using Markovian property as follows: developing the a posteriori probability compared to a pixel s, we choose as a new value in s the one that maximizes the conditional probability $P(X=x\left| Y=y\right. )$, which can be written as,

$$\begin{aligned} X^* = \arg \{\max \limits _X \left[ P(y|x=x_s)P(x_s)\right] \}, \end{aligned}$$

(4)

here, $P(y|x=x_s)$ is the probability that the data point y is observed for the given class of the configuration x in the site s, whereas $P(x_s)$ denotes the a priori probability of the configuration $x_s$. To calculate the probability$P(y|x=x_s)$, a multivariate Gaussian distribution with mean vector $\mu _s$ and covariance matrix $\varSigma _s$ is assumed for class in $x_s$:

$$\begin{aligned} P(y|x=x_{s} )=\frac{1}{2\pi ^{d/2} \left| \varSigma _s \right| ^{1/2} } \exp [-\frac{1}{2} (y_s -\mu _s )^T \varSigma _{s}^{-1} (y_s -\mu _s )], \end{aligned}$$

(5)

where d is the number of spectral bands.

The common covariance matrix is $\varSigma =\frac{1}{L} \sum _{i=1}^{L}\varSigma _i$.

Substituting (4) into (5), yields,

$$\begin{aligned} X^{*} = \arg \{\max \limits _{X} [C\exp (-E(X|Y))]\}, \end{aligned}$$

(6)

where $C={1}/{Z_T (2\pi )^{d/2} }$, ${Z_T}$ is a normalizing constant depends on the temperature T and

$$ E(X|Y)=\frac{1}{T} U(x_{s})+\frac{1}{2} (y_{s} -\mu _{s} )^{T} \varSigma _{s}^{-1} (y_{s} -\mu _{s} )+\frac{1}{2} \ln (|\varSigma _{s} |). $$

Since the exponential function is monotonic and C is a constant that is independent of X, (6) can be reduced to

$$\begin{aligned} X^{*} = \arg \{\min \limits _{X} [E(X|Y)]\}. \end{aligned}$$

(7)

3.2 The Developed ICM Method with Contextual Constraints

The formalism of Markov Random Fields makes it possible to introduce, in a flexible way, the constraints of spatial context through their modeling by some potential functions. In addition to the constraint of the neighbourhood (regularization or smoothing constraint) we have introduced another constraint which is that of the contour (segmentation) [7] in order to minimize more the function of energy E in the classification. The expression of the function of energy, corresponding to the constraints used in the modeling of the a priori probability implemented in our application is as follow:

$$\begin{aligned} E(X|Y)\propto \frac{1}{T} U(x_s)+f(y_s ,\mu _s ,\varSigma _s), \end{aligned}$$

(8)

where

$$\begin{aligned} U(x_s)=\sum _{all\_ constraints}U_{constraint} = U_{smooth}(x_s)+U_{contour}(x_s). \end{aligned}$$

(9)

For the constraint of regularization, the class the most present in the neighborhood of the pixel is favored. For the constraint of contour, the image of contours used is obtained through a segmentation process cited in [7].

Throughout the algorithm, we will decrease T, nor too quickly to avoid getting blocked around a local minimum, nor too slowly if we want to have a result in a reasonable time.

4 Result and Discussion

4.1 Study Area

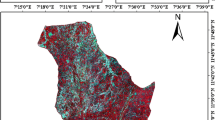
The study area is the date palm grove of Mezguita (Fig. 2), in the Draa River Valley, Morocco. It has an extension of 44 km$^2$. The mean altitude is near 900 m above sea level. The area is characterized by a prevalence of small property. 85.8 % of farms have a surface lower than 2 ha and only 5.3 % of farms have a surface higher than 5 ha. In this very fragmented zone where date palms coexist with other crops.

4.2 Satellite Data

A 9 km $\times$ 4.9 km Worldview-2 (WV2) image of the Mezguita Oasis (Fig. 2), acquired on 13 April 2012 at 11:39 UTM was used. The acquisition was slightly off-nadir at 83.2 satellite elevation. The image was supplied at the nominal spatial resolution of 0.50 m/pixel and 2 m/pixel for the panchromatic and multispectral bands, respectively.

Fig. 2.

Worldview-2 image of the Mezguita Oasis

4.3 Image Pre-processing

The acquired WV-2 image was standard ortho ready level and radiometrically corrected. It was converted to top-of-atmosphere spectral radiance using the procedure described in [8]. The resulting image was atmospherically corrected to obtain surface reflectances by mean of FLAASH (Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes), a first-principles atmospheric correction tool that corrects wavelengths in the visible through near-infrared and shortwave infrared regions [9]. Normally, palms are mixed with the rest of crops and soil uses, and irregularly arranged, which necessitates the highest possible level of detail. This is possible thanks to the panchromatic image with a resolution of 50 cm per pixel, but at the same time we would lose all the 8 spectral information bands of WV-2 satellite. That is why we chose a process of fusion where the multispectral bands were resampled through the Gram-Smith Spectral sharpening with the panchromatic band. Thus, an image is obtained that has not only a higher spatial resolution, but also all the spectral information. In addition to the loss or possible distortion of the spectral information which can occur during this process, there is still another problem arises: the considerable size of the generated image, which forces to use very powerful equipment to reduce the duration of treatment. The fusion method used was developed in [10] This technique solves the two most important problems in the image fusion: on the one hand the color distortion and, on the other hand, the operator dependence. It is about an adjustment by the ordinary least squares (OLS) method between the gray levels of the original multi-spectral images, the panchromatic and the fused bands to improve the color representation (Fig. 3).

Fig. 3.

Fusion process (C) of multi-spectral bands (B) with panchromatic band (A)

4.4 Classification Results

In this section we present the results obtained, first, with the proposed supervised contextual classification represented in the Fig. 4 by comparing it with the most commonly used supervised classification namely maximum likelihood (MLC). Thereafter, we show the interest of the use of shape and shadow direction information to refine the result of the contextual classification by masking the palm trees.

Fig. 4.

[4-3-2] bands color composite and Classified result map [palm tree (blue); shadow (cyan)] (Color figure online)

The confusion matrix in Table 1 shows the results of the validation polygons compared to the classified image. The main diagonal refers to the well-classified areas. In addition, we have calculated the producer’s accuracy and at the user’s accuracy (Table 2). The first accuracy refers to the probability for a given type of land cover to be well classified, and the second refers to the probability of an object on the classified image actually belong to the class it represents

Table 1. Confusion matrix of the proposed ICM classification

Generally, it could be said that the non-contextual results did not allow good palm trees class detection (73.2 % total accuracy using ENVI Software). On the contrary, for the ICM method a total palm trees accuracy of 83.4 % was achieved. After having the classified map, the palm trees will be detected based on the shape (circular or elliptical), the orientation angle and the distance between the centers of the adjacent labeled objects of the palm trees class and shadow class to select the potential palm trees. For the choice of the angle of orientation, it was chosen experimentally between $40^o$ and $50^o$ Fig. 5. The decision may be reformulated as below.

$$\begin{aligned} Decision = AND( Criterion_{shape} ; Criterion_{dist-palm-shadow} ; Criterion_{angle}) \end{aligned}$$

(10)

Tree objects are identified according to their geometric properties (shape rule) as they define compact and elliptical objects and according to the adjacency between palm tree class and shadow class (distance rule). Also, tree objects depend to the directional existence of shadow according to the sun illumination represented by the third rule of angle orientation.

As expected, with the use of the shape and shadow information. This accuracy shows improved to reach 88.1 %.

Fig. 5.

Experimental angle interval of shadow orientation

Table 2. Palm trees producer’s accuracy and user’s accuracy

5 Conclusion

In this paper we have proposed a new supervised classification based on the Model of Markov Region and derived from the ICM (Iterated Conditional Mode). We have added a post-classification decision criterion based on shape, orientation angle and the distance, an improvement was achieved. The application of this method for the detection of palm trees is promising, however, the case of overlapping palm trees still significant issue for further investigation.