Abstract
Accountability is a critical requirement of any deployed voting system as it allows unequivocal identification of misbehaving parties, including authorities. In this paper, we propose the first game-based definition of accountability and demonstrate its usefulness by applying it to the sElect voting system (Küsters et al., 2016) – a voting system that relies on no other cryptographic primitives than digital signatures and public key encryption.
We strengthen our contribution by proving accountability for sElect in the EasyCrypt proof assistant. As part of this, we identify a few errors in the proof for sElect as presented by Küsters et al. (2016) for their definition of accountability.
Finally, we reinforce the known relation between accountability and verifiability, and show that it is still maintained by our new game-based definition of accountability.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The EasyCrypt code can be accessed from https://github.com/mortensol/acc-select.
- 2.
Absenting voters verify that their identifier is not included on the list published by the \(\textsf{AS}\).
- 3.
In the game, we use the notation “\(\textsf {Require}\)” for
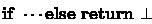 .
.
References
Abdalla, M., Bellare, M., Rogaway, P.: DHIES: an encryption scheme based on the Diffie-Hellman problem. Contributions to IEEE P1363a (Sep 1998)
Adida, B.: Helios: web-based open-audit voting. In: van Oorschot, P.C. (ed.) USENIX Security 2008, pp. 335–348. USENIX Association (Jul / Aug 2008)
Barthe, G., Dupressoir, F., Grégoire, B., Kunz, C., Schmidt, B., Strub, P.-Y.: EasyCrypt: a tutorial. In: Aldini, A., Lopez, J., Martinelli, F. (eds.) FOSAD 2012-2013. LNCS, vol. 8604, pp. 146–166. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10082-1_6
Bernhard, D., Cortier, V., Galindo, D., Pereira, O., Warinschi, B.: A comprehensive analysis of game-based ballot privacy definitions. Cryptology ePrint Archive, Report 2015/255 (2015). https://eprint.iacr.org/2015/255
Bruni, A., Giustolisi, R., Schürmann, C.: Automated analysis of accountability. In: Nguyen, P.Q., Zhou, J. (eds.) ISC 2017. LNCS, vol. 10599, pp. 417–434. Springer, Heidelberg (Nov (2017)
Cortier, V., Dragan, C.C., Dupressoir, F., Schmidt, B., Strub, P.Y., Warinschi, B.: Machine-checked proofs of privacy for electronic voting protocols. In: 2017 IEEE Symposium on Security and Privacy, pp. 993–1008. IEEE Computer Society Press (May 2017). https://doi.org/10.1109/SP.2017.28
Cortier, V., Dragan, C.C., Dupressoir, F., Warinschi, B.: Machine-checked proofs for electronic voting: Privacy and verifiability for belenios. In: Chong, S., Delaune, S. (eds.) CSF 2018 Computer Security Foundations Symposium, pp. 298–312. IEEE Computer Society Press (2018). https://doi.org/10.1109/CSF.2018.00029
Cortier, V., Lallemand, J., Warinschi, B.: Fifty shades of ballot privacy: privacy against a malicious board. In: Jia, L., Küsters, R. (eds.) CSF 2020 Computer Security Foundations Symposium, pp. 17–32. IEEE Computer Society Press (2020). https://doi.org/10.1109/CSF49147.2020.00010
Cortier, V., Gaudry, P., Glondu, S.: Belenios: a simple private and verifiable electronic voting System, pp. 214–238 (04 2019). https://doi.org/10.1007/978-3-030-19052-1_14
Drăgan, et al.: Machine-checked proofs of privacy against malicious boards for selene & co. In: 2022 IEEE 35th Computer Security Foundations Symposium (CSF), pp. 335–347 (2022). https://doi.org/10.1109/CSF54842.2022.9919663
Hirschi, L., Schmid, L., Basin, D.A.: Fixing the achilles heel of E-voting: The bulletin board. In: Küsters, R., Naumann, D. (eds.) CSF 2021 Computer Security Foundations Symposium, pp. 1–17. IEEE Computer Society Press (2021). https://doi.org/10.1109/CSF51468.2021.00016
Khazaei, S., Moran, T., Wikström, D.: A mix-net from any CCA2 secure cryptosystem. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 607–625. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_37
Kiayias, A., Zacharias, T., Zhang, B.: End-to-end verifiable elections in the standard model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 468–498. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_16
Kiayias, A., Zacharias, T., Zhang, B.: Ceremonies for end-to-end verifiable elections. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 305–334. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_11
Künnemann, R., Esiyok, I., Backes, M.: Automated verification of accountability in security protocols. In: Delaune, S., Jia, L. (eds.) CSF 2019 Computer Security Foundations Symposium, pp. 397–413. IEEE Computer Society Press (2019). https://doi.org/10.1109/CSF.2019.00034
Künnemann, R., Garg, D., Backes, M.: Accountability in the decentralised-adversary setting. In: Küsters, R., Naumann, D. (eds.) CSF 2021 Computer Security Foundations Symposium, pp. 1–16. IEEE Computer Society Press (2021). https://doi.org/10.1109/CSF51468.2021.00007
Küsters, R., Müller, J., Scapin, E., Truderung, T.: sElect: a lightweight verifiable remote voting system. In: Hicks, M., Köpf, B. (eds.) CSF 2016 Computer Security Foundations Symposium, pp. 341–354. IEEE Computer Society Press (2016). https://doi.org/10.1109/CSF.2016.31
Küsters, R., Truderung, T., Vogt, A.: Accountability: definition and relationship to verifiability. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 526–535. ACM Press (Oct 2010). https://doi.org/10.1145/1866307.1866366
Morio, K., Künnemann, R.: Verifying accountability for unbounded sets of participants. In: Küsters, R., Naumann, D. (eds.) CSF 2021 Computer Security Foundations Symposium, pp. 1–16. IEEE Computer Society Press (2021). https://doi.org/10.1109/CSF51468.2021.00032
Ryan, P.Y.A., Rønne, P.B., Iovino, V.: Selene: voting with transparent verifiability and coercion-mitigation. In: Clark, J., Meiklejohn, S., Ryan, P.Y.A., Wallach, D., Brenner, M., Rohloff, K. (eds.) FC 2016. LNCS, vol. 9604, pp. 176–192. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53357-4_12
SwissPost: Swiss post voting system. https://gitlab.com/swisspost-evoting (2022)
Acknowledgment
T. Haines is the recipient of an Australian Research Council Australian Discovery Early Career Award (project number DE220100595). C. C. Drăgan is supported by EPSRC grant EP/W032473/1 (AP4L), EU Horizon grants 101069688(CONNECT) and 101070627 (REWIRE). P. Rønne received funding from the France 2030 program managed by the French National Research Agency under grant agreement No. ANR-22-PECY-0006.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A Sketch of Proof of Theorem 1
We now sketch the proof of Theorem 1. We begin by defining two new games: a fairness game \( G_{f} \) and a completeness game \( G_{c} \). These games are almost identical to the original security game, with the exception that in \( G_{f} \), we remove the variable \( e_{c} \) from the experiment and only consider the fairness aspect of accountability, while in \( G_{c} \), we remove the variable \( e_{f} \) and only consider the completeness aspect of accountability. Let \( E_{f} \) resp. \( E_{c} \) be the event that the game \( G_{f} \) resp. \( G_{c} \) returns 1. It is straightforward to see that  . Thus, the adversary has two possibilities to win. Either \( \textsf{Judge} \) has blamed an innocent party, or it has blamed no one, but the result is inconsistent with the honest votes. We analyze the fairness and completeness aspects separately, and argue that the adversary has zero probability of winning the fairness game and negligible probability of winning the completeness game.
. Thus, the adversary has two possibilities to win. Either \( \textsf{Judge} \) has blamed an innocent party, or it has blamed no one, but the result is inconsistent with the honest votes. We analyze the fairness and completeness aspects separately, and argue that the adversary has zero probability of winning the fairness game and negligible probability of winning the completeness game.
We begin with fairness. We will consider each way in which the judge may blame a party and show that it will never blame a party that did not misbehave. Recall the various checks performed by the judge: The judge first checks that the public keys used by the authentication server and the mix servers are valid. If not, it will blame the voting authority as it allowed the election to run with invalid keys. Note that \( \textsf{Bad} \) will also blame the voting authority if the keys are invalid (but not otherwise), meaning that the voting authority will only be blamed by the judge if it indeed misbehaved. As invalid keys will result in the voting authority being blamed by both the judge and by \( \textsf{Bad} \), we assume for the remainder of the proof that all the public keys are valid.
The judge then checks that the bulletin board \( \textsf{BB}_{vote}\) is valid, i.e. that it contains at most \( N_{v} \) elements and that its contents are in lexicographic order and duplicate-free. If this check fails, the judge blames the authentication server. If this is the case, the authentication server will also be blamed by \( \textsf{Bad} \), ensuring that if \( \textsf{AS} \) is blamed for producing an invalid board, it must indeed have misbehaved. Next, the judge checks that the output of each mix server contains at most as many elements as in its received input and that the output of each mix server is duplicate free and in lexicographic order. Since an honest mixer filters out duplicates and sorts the output list, it will always pass this check.
The judge then checks, for all ciphertext and signature pairs in the evidence list whether or not there is a ballot with a valid signature that is not present on \( \textsf{BB}_{vote}\). Since an honest authentication server only authenticates the first ballot from each voter, and posts all these on the bulletin board, it will always pass this check. Note that if a dishonest voter blames the authentication server with valid evidence, the \( \textsf{Bad} \) algorithm will also blame the authentication server, and thus the judge will not blame the authentication server unless it is also blamed by \( \textsf{Bad} \). Finally, \( \textsf{Judge} \) checks, for any triple \( (\textsf{mpk}_{i}, \alpha _{i+1}, r_{i}) \), whether or not  is in the input to the ith mix server, but \( \alpha _{i+1} \) is not in its output. Since the encryption system is correct,
is in the input to the ith mix server, but \( \alpha _{i+1} \) is not in its output. Since the encryption system is correct,  will decrypt to \(\alpha _{i+1}\) and since an honest mix server does not remove any ciphertexts other than duplicates, it will always pass this check. In summary, \( \textsf{Judge} \) will never blame an honestly behaving party, and thus, the adversary has zero probability of winning the fairness game.
will decrypt to \(\alpha _{i+1}\) and since an honest mix server does not remove any ciphertexts other than duplicates, it will always pass this check. In summary, \( \textsf{Judge} \) will never blame an honestly behaving party, and thus, the adversary has zero probability of winning the fairness game.
We now move on to completeness and bound the adversarial advantage in the completeness game, i.e. that if extra ballots are added or honest voters’ ballots are dropped, the judge will, with overwhelming probability, hold someone accountable. Fairness ensures that the blamed party actually misbehaved.
We begin with the first criterion for completeness, i.e. that the number of ballots on \( \textsf{BB}_{vote}\) is not greater than the number of eligible voters. This follows from the second check of the \( \textsf{Judge} \) algorithm, where it checks if the bulletin board is valid. The second criterion (that the number of votes on \( \textsf{BB}_{dec}\) is not greater than the number of cast ballots) follows from the judge checking that the output of each mix server contains at most as many elements as its input.
Now consider the criterion that says that all honest votes are in the multiset of votes output by the last mix server (i.e. \( \textsf{BB}_{dec}\)). Every honest voter checks, using \( \textsf{VSDVerify} \), that their ballot appears in \( \textsf{BB}_{vote}\). If not there, they output the token \( \sigma \) given to them by the authentication server. This, in turn, causes the authentication server to be blamed by the judge. If \( \textsf{AS}\) was not blamed, we know that all honest ballots were present in \( \textsf{BB}_{vote}\). If any honest ballot is dropped by one of the mix servers, this will be detected by \( \textsf{VSDVerify} \), which will output some evidence that this mix server misbehaved, which in turn causes this mix server to be blamed by the judge.
Now, the adversary has one possibility of winning the completeness game, namely if two (or more) voters have cast the same vote, and their sampled nonces happen to be equal. In this case, the adversary may drop all but one of these ballots without it being detected. To analyze this situation, we slightly modify the completeness game. We call the new game \( G_{c}' \) and let \( E_{c}' \) be the probability that \( G_{c}' \) returns 1. The difference from \( G_{c} \) to \( G_{c}' \) is that in \( G_{c}' \), we keep track of the nonces that are sampled when the adversary calls the vote oracle, and only sample new nonces from the set of nonces that have not been used earlier. The two games are equivalent unless there is a collision in the first game, hence 
In \( G_{c}' \), as there are no collisions in the nonces, any ballot that is dropped by the adversary will be detected by \( \textsf{VSDVerify} \), which in turns causes the judge to blame the misbehaving party. In other words, in \( G_{c}' \), the adversary will have zero probability of winning, so  . Thus, the probability that the adversary wins the completeness game is bounded by
. Thus, the probability that the adversary wins the completeness game is bounded by  . As the adversary has zero probability of winning the fairness game, and the probability of winning the accountability game is bounded by the sum of winning the fairness game and the completeness game, we arrive at the conclusion of Theorem 1 that the advantage is bounded by the collision probability. By the birthday paradox the collission probability is bounded by \( \frac{q_v(q_v-1)}{2 \cdot |\textsf{N}|} \), where \( q_v\) is the number of queries vote oracle queries and \( \textsf{N}\) is the nonce space.
. As the adversary has zero probability of winning the fairness game, and the probability of winning the accountability game is bounded by the sum of winning the fairness game and the completeness game, we arrive at the conclusion of Theorem 1 that the advantage is bounded by the collision probability. By the birthday paradox the collission probability is bounded by \( \frac{q_v(q_v-1)}{2 \cdot |\textsf{N}|} \), where \( q_v\) is the number of queries vote oracle queries and \( \textsf{N}\) is the nonce space.
Appendix B Proof for Theorem 2
The proof of the theorem follows from analyzing Fairness and Completeness.
Lemma 1
(Fairness). The judge J is computationally fair in \( \mathcal {P}(n,m,\mu , p^{verif}_{voter},p^{verif}_{abst})\).
Proof
The proof is essentially the same as for sElect in [17] for the voting phase but relies on \(\textsf{GBA}\) in the mixing and decryption phases.
Consider what happens if the voter makes a complaint and the judge blames both the party accused and the voter (J2). Since the bulletin board is honest and the channel is authenticated the voter must really have made the complaint. There are two cases. If the voter is dishonest the verdict is clearly true. If the voter is honest, the correctness of the verdict follows from the voter verification correctness of the protocol either because the person it blamed has misbehaved or because the authentication server did not send a valid confirmation. (J2) covers both the case where the voter’s ballot is dropped and when it is added.
Case (J1) is covered by \(\textsf{GBA}\). Since the scheme has \(\textsf{GBA}\) it follows that the adversary cannot make either of these conditions trigger when the party ran its honest program, otherwise \(\textsf{GBA}\) would not hold.
Lemma 2
(Completeness). For every instance \(\pi \) of \(\mathcal {P}(n,m,\mu , p^{verif}_{voter},p^{verif}_{abst})\), we have
with overwhelming probability as a function of l.
Again, the proof is essentially the same as for sElect in the voting phase but relies on \(\textsf{GBA}\) in the mixing and decryption phases. We need to show that the following probabilities are bounded for every i: a) \(Pr\big [\pi (1^l) \rightarrow (\chi _i \wedge \lnot dis(v_i) \wedge \lnot dis(AS) ) \big ]\), b) \(Pr\big [\pi (1^l) \rightarrow (\chi '_i \wedge \lnot dis(v_i) \wedge \lnot dis(AS)) \big ]\), c) \(Pr\big [\pi (1^l) \rightarrow (\lnot \gamma _k \wedge \lnot \chi \rightarrow dis(\textsf{VA}) | dis(\textsf{AS}) | dis(\textsf{DA}_i)_{i=1}^q | dis(\textsf{MS}_j)_{j=1}^m) \big ]\). The first two probabilities are equal to zero as noted in the sElect proof [17]. The last probability is \(\delta ^k\) bounded by the completeness component of \(\textsf{GBA}\). This is immediate when \(p^{verif}_{voter}\) is equal to one since our definition assumes all honest voters vote and verify; when \(p^{verif}_{voter}\) is lower this is more complicated and requires guessing ahead of time which voters will verify. This can be achieved using standard techniques from complexity leveraging.
Appendix C Proof for Theorem 3
Proof
Consider an adversary \(\mathcal {A}\) against  . We start by running \(\mathcal {A}\) getting the output \(\textsf{pd}\) which we use for \(\mathcal {B}\) in addition to an honestly generated signing keypair for \(\textsf{AS}\). We then make a random guess about which voters \(\mathcal {A}\) is going to ask to verify. The probability of guessing correctly is at least \(1/2^{|\mathcal {I}|}\). Now, we keep running \(\mathcal {A}\) to choose honestly cast votes and creating the bulletin board \(\textsf{BB}\). Every time the vote oracle is called and we guessed the voter is going to verify, we let \(\mathcal {B}\) query the same and forward the output to \(\mathcal {A}\). If we guessed that the voter is not going to verify, we simply honestly generate the ballot and send it to \(\mathcal {A}\) without \(\mathcal {B}\) querying the vote oracle. We use the board \(\textsf{BB}\) output by \(\mathcal {A}\) in addition to honestly generated signatures for \(\textsf{AS}\). Since the signature scheme is perfectly correct, the signatures will verify in lines 4–7 of
. We start by running \(\mathcal {A}\) getting the output \(\textsf{pd}\) which we use for \(\mathcal {B}\) in addition to an honestly generated signing keypair for \(\textsf{AS}\). We then make a random guess about which voters \(\mathcal {A}\) is going to ask to verify. The probability of guessing correctly is at least \(1/2^{|\mathcal {I}|}\). Now, we keep running \(\mathcal {A}\) to choose honestly cast votes and creating the bulletin board \(\textsf{BB}\). Every time the vote oracle is called and we guessed the voter is going to verify, we let \(\mathcal {B}\) query the same and forward the output to \(\mathcal {A}\). If we guessed that the voter is not going to verify, we simply honestly generate the ballot and send it to \(\mathcal {A}\) without \(\mathcal {B}\) querying the vote oracle. We use the board \(\textsf{BB}\) output by \(\mathcal {A}\) in addition to honestly generated signatures for \(\textsf{AS}\). Since the signature scheme is perfectly correct, the signatures will verify in lines 4–7 of  .
.
We now run \(\mathcal {O}\textsf{Verify}\) for \(\mathcal {B}\) which will call verification for all voters used in the oracle calls in  . We can use the outputs to \(\mathcal {A}\)’s calls to the verification oracle. Here we assume that we guessed the verifiers correctly and, further, in this case the two sets of verifying voters will be the same in the two experiments. For the sake of the proof, we will abort if they do not match, hence the degradation factor in the advantage. Now with probability
. We can use the outputs to \(\mathcal {A}\)’s calls to the verification oracle. Here we assume that we guessed the verifiers correctly and, further, in this case the two sets of verifying voters will be the same in the two experiments. For the sake of the proof, we will abort if they do not match, hence the degradation factor in the advantage. Now with probability  in
in  we will have no complaints from the individual verification, the universal verification will be successful and we have \(\lnot (|\mathcal {I}|\ge |\textsf{BB}|_{submit}|\ge |\textsf{BB}|_{res}|\wedge \textsf{V}[\textsf{Checked}]\subseteq _{ms}\textsf{BB}|_{res})\). Using that the scheme is accountability-verifiability-correct in
we will have no complaints from the individual verification, the universal verification will be successful and we have \(\lnot (|\mathcal {I}|\ge |\textsf{BB}|_{submit}|\ge |\textsf{BB}|_{res}|\wedge \textsf{V}[\textsf{Checked}]\subseteq _{ms}\textsf{BB}|_{res})\). Using that the scheme is accountability-verifiability-correct in  all individual verification will also produce no blame since the signatures will verify by perfect correctness, and, finally, again by accountability-verifiability-correctness and successful universal verification, no blame will be output by \(\textsf{Judge}\), i.e. \(|B|=0\). Since the votes from the verifying voters, \(\textsf{V}[\textsf{Checked}]\), in
all individual verification will also produce no blame since the signatures will verify by perfect correctness, and, finally, again by accountability-verifiability-correctness and successful universal verification, no blame will be output by \(\textsf{Judge}\), i.e. \(|B|=0\). Since the votes from the verifying voters, \(\textsf{V}[\textsf{Checked}]\), in  exactly corresponds to the votes from the oracle vote calls in
exactly corresponds to the votes from the oracle vote calls in  and \(|\textsf{BB}|_{submit}|=|\textsf{BB}_{vote}| \) and \(\textsf{BB}|_{res}=\textsf{BB}_{dec}\) we exactly get the winning condition \((\lnot (n \ge |\textsf{BB}_{vote}| \ge |\textsf{BB}_{dec}| \wedge V \subseteq \textsf{BB}_{dec}) \wedge B = \bot )\) in
and \(|\textsf{BB}|_{submit}|=|\textsf{BB}_{vote}| \) and \(\textsf{BB}|_{res}=\textsf{BB}_{dec}\) we exactly get the winning condition \((\lnot (n \ge |\textsf{BB}_{vote}| \ge |\textsf{BB}_{dec}| \wedge V \subseteq \textsf{BB}_{dec}) \wedge B = \bot )\) in  .
.
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Drăgan, C.C., Dupressoir, F., Gjøsteen, K., Haines, T., Rønne, P.B., Solberg, M.R. (2024). Machine-Checked Proofs of Accountability: How to sElect Who is to Blame. In: Tsudik, G., Conti, M., Liang, K., Smaragdakis, G. (eds) Computer Security – ESORICS 2023. ESORICS 2023. Lecture Notes in Computer Science, vol 14346. Springer, Cham. https://doi.org/10.1007/978-3-031-51479-1_24
Download citation
DOI: https://doi.org/10.1007/978-3-031-51479-1_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-51478-4
Online ISBN: 978-3-031-51479-1
eBook Packages: Computer ScienceComputer Science (R0)






 .
.