Abstract
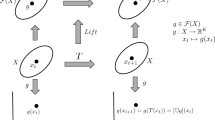
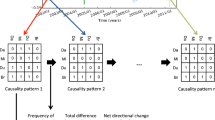
Dynamical networks are a framework commonly used to model large networks of interacting time-varying components such as power grids and epidemic disease networks. The connectivity structure of dynamical networks play a key role in enabling many interesting behaviours such as synchronisation and chimeras. However, dynamical networks can also be vulnerable to network attack, where the connectivity structure is externally altered. This can cause sudden failure and loss of stability in the network. The ability to detect these network attacks is useful in troubleshooting and preventing system failure. Recently, a backpropagation regression method inspired by RNN training algorithms was proposed to infer both local node dynamics and connectivity structure from measured node signals. This paper explores the application of backpropagation regression for fault detection in dynamical networks. We construct separate models for local dynamics and coupling structure to perform short-term freerun predictions. Due to the separation of models, abnormal increases in prediction error can be attributed to changes in the network structure. Automatic detection is achieved by comparing prediction error statistics across two windows that span a period before and after a network attack. This method is tested on a simulated dynamical network of chaotic Lorenz oscillators undergoing gradual edge corruption via three different processes: edge swapping, moving and deletion. We demonstrate that the correlation between increased prediction error and the occurrence of edge corruption can be used to reliably detect both the onset and approximate location of the attack within the network.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Abrams, D.M., Strogatz, S.H.: Chimera states for coupled oscillators. Phys. Rev. Lett. 93(17), 174102 (2004)
Andreev, A., Frolov, N., Pisarchik, A., Hramov, A.: Chimera state in complex networks of bistable Hodgkin-Huxley neurons. Phys. Rev. E 100(2), 022224 (2019)
Banerjee, A., Hart, J.D., Roy, R., Ott, E.: Machine learning link inference of noisy delay-coupled networks with optoelectronic experimental tests. Phys. Rev. X 11(3), 031014 (2021)
Banerjee, A., Pathak, J., Roy, R., Restrepo, J.G., Ott, E.: Using machine learning to assess short term causal dependence and infer network links. Chaos Interdisc. J. Nonlinear Sci. 29(12), 121104 (2019)
Casadiego, J., Nitzan, M., Hallerberg, S., Timme, M.: Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun. 8(1), 1–10 (2017)
Dashtdar, M., Dashti, R., Shaker, H.R.: Distribution network fault section identification and fault location using artificial neural network. In: 2018 5th International Conference on Electrical and Electronic Engineering (ICEEE), pp. 273–278. IEEE (2018)
Eroglu, D., Tanzi, M., van Strien, S., Pereira, T.: Revealing dynamics, communities, and criticality from data. Phys. Rev. X 10(2), 021047 (2020)
Hota, A.R., Sneh, T., Gupta, K.: Impacts of game-theoretic activation on epidemic spread over dynamical networks. SIAM J. Control. Optim. 60(2), S92–S118 (2021)
Izhikevich, E.M.: Dynamical systems in neuroscience. MIT press (2007)
Jaeger, H.: The “echo state” approach to analysing and training recurrent neural networks-with an erratum note. Bonn, Germany: German National Research Center for Information Technology Gesellschaft für Mathematik und Datenverarbeitung mbH (GMD) Technical Report 148, 13 (2001)
Kohar, V., Sinha, S.: Emergence of epidemics in rapidly varying networks. Chaos Solitons Fractals 54, 127–134 (2013)
Kornilov, M., Sysoev, I., Astakhova, D., Kulminsky, D., Bezruchko, B., Ponomarenko, V.: Reconstruction of the coupling architecture in the ensembles of radio-engineering oscillators by their signals using the methods of granger causality and partial directed coherence. Radiophys. Quantum Electron. 63(7), 542–556 (2020)
Lorenz, E.N.: Deterministic nonperiodic flow. J. Atmos. Sci. 20(2), 130–141 (1963)
Majdandzic, A., et al.: Multiple tipping points and optimal repairing in interacting networks. Nat. Commun. 7(1), 1–10 (2016)
Masuda, N., Lambiotte, R.: A guide to temporal networks. World Scientific (2016)
Muhammed, T., Shaikh, R.A.: An analysis of fault detection strategies in wireless sensor networks. J. Netw. Comput. Appl. 78, 267–287 (2017)
Napoletani, D., Sauer, T.D.: Reconstructing the topology of sparsely connected dynamical networks. Phys. Rev. E 77(2), 026103 (2008)
Pasqualetti, F., Dörfler, F., Bullo, F.: Attack detection and identification in cyber-physical systems. IEEE Trans. Autom. Contr. 58(11), 2715–2729 (2013)
Rosenblum, M., Frühwirth, M., Moser, M., Pikovsky, A.: Dynamical disentanglement in an analysis of oscillatory systems: an application to respiratory sinus arrhythmia. Phil. Trans. R. Soc. A 377(2160), 20190045 (2019)
Sachtjen, M., Carreras, B., Lynch, V.: Disturbances in a power transmission system. Phys. Rev. E 61(5), 4877 (2000)
Shandilya, S.G., Timme, M.: Inferring network topology from complex dynamics. New J. Phys. 13(1), 013004 (2011)
Small, M., Tse, C.K.: Minimum description length neural networks for time series prediction. Phys. Rev. E 66(6), 066701 (2002)
Stepaniants, G., Brunton, B.W., Kutz, J.N.: Inferring causal networks of dynamical systems through transient dynamics and perturbation. Phys. Rev. E 102(4), 042309 (2020)
Takens, F.: Detecting strange attractors in turbulence. In: Rand, D., Young, L.-S. (eds.) Dynamical Systems and Turbulence, Warwick 1980. LNM, vol. 898, pp. 366–381. Springer, Heidelberg (1981). https://doi.org/10.1007/BFb0091924
Tan, E., Corrêa, D., Stemler, T., Small, M.: Backpropagation on dynamical networks. arXiv preprint arXiv:2207.03093 (2022)
Valencia, M., Martinerie, J., Dupont, S., Chavez, M.: Dynamic small-world behavior in functional brain networks unveiled by an event-related networks approach. Phys. Rev. E 77(5), 050905 (2008)
Wang, J., Rong, L., Zhang, L., Zhang, Z.: Attack vulnerability of scale-free networks due to cascading failures. Physica A 387(26), 6671–6678 (2008)
Wang, W.X., Lai, Y.C., Grebogi, C.: Data based identification and prediction of nonlinear and complex dynamical systems. Phys. Rep. 644, 1–76 (2016)
Weistuch, C., Agozzino, L., Mujica-Parodi, L.R., Dill, K.A.: Inferring a network from dynamical signals at its nodes. PLoS Comput. Biol. 16(11), e1008435 (2020)
Wu, B., Zhou, D., Fu, F., Luo, Q., Wang, L., Traulsen, A.: Evolution of cooperation on stochastic dynamical networks. PLoS ONE 5(6), e11187 (2010)
Wu, H.S.: A survey of research on anomaly detection for time series. In: 2016 13th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), pp. 426–431. IEEE (2016)
Xia, Y., Fan, J., Hill, D.: Cascading failure in Watts-Strogatz small-world networks. Physica A 389(6), 1281–1285 (2010)
Xia, Y., Hill, D.J.: Attack vulnerability of complex communication networks. IEEE Trans. Circuits Syst. II Express Briefs 55(1), 65–69 (2008)
Yang, L.X., Jiang, J.: Impacts of link addition and removal on synchronization of an elementary power network. Physica A 479, 99–107 (2017)
Zenisek, J., Holzinger, F., Affenzeller, M.: Machine learning based concept drift detection for predictive maintenance. Comput. Ind. Eng. 137, 106031 (2019)
Zhang, J.S., Xiao, X.C.: Predicting chaotic time series using recurrent neural network. Chin. Phys. Lett. 17(2), 88 (2000)
Zhang, S., Tong, H., Xu, J., Maciejewski, R.: Graph convolutional networks: a comprehensive review. Comput. Soc. Netw. 6(1), 1–23 (2019). https://doi.org/10.1186/s40649-019-0069-y
Zhu, Y., Zheng, Z., Yang, J.: Chimera states on complex networks. Phys. Rev. E 89(2), 022914 (2014)
Acknowledgements
E.T. is supported by a Robert and Maude Gledden Postgraduate Research Scholarship and Australian Government Research Training Program Scholarship at The University of Western Australia. M.S. and D.C.C. acknowledge the support of the Australian Research Council through the Centre for Transforming Maintenance through Data Science (grant number IC180100030), funded by the Australian Government.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Tan, E., Corrêa, D.C., Stemler, T., Small, M. (2022). Machine Learning Inspired Fault Detection of Dynamical Networks. In: Aziz, H., Corrêa, D., French, T. (eds) AI 2022: Advances in Artificial Intelligence. AI 2022. Lecture Notes in Computer Science(), vol 13728. Springer, Cham. https://doi.org/10.1007/978-3-031-22695-3_33
Download citation
DOI: https://doi.org/10.1007/978-3-031-22695-3_33
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-22694-6
Online ISBN: 978-3-031-22695-3
eBook Packages: Computer ScienceComputer Science (R0)