Abstract
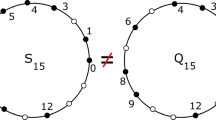
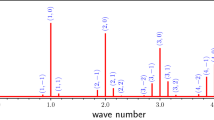
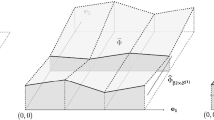
This paper contributes to the emergent area of Periodic Geometry, which studies continuous spaces of solid crystalline materials (crystals) by new methods of metric geometry. Since crystal structures are determined in a rigid form, their strongest practical equivalence is rigid motion or isometry preserving inter-point distances. The most fundamental model of any crystal is a periodic set of points at all atomic centers. The previous work introduced an infinite sequence of density functions that are continuous isometry invariants of periodic point sets. These density functions turned out to be highly non-trivial even in dimension 1 for periodic sequences of points in the line. This paper fully describes the density functions of any periodic sequence and their symmetry properties. The explicit description confirms coincidences of density functions that were previously computed via finite samples.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Anosova, O., Kurlin, V.: Introduction to periodic geometry and topology (2021). https://arxiv.org/abs/2103.02749
Anosova, O., Kurlin, V.: Algorithms for continuous metrics on periodic crystals (2022). https://arxiv.org/abs/2205.15298
Bright, M., Cooper, A.I., Kurlin, V.: Geographic-style maps for 2-dimensional lattices (2021). https://arxiv.org/abs/2109.10885
Bright, M., Cooper, A.I., Kurlin, V.: Welcome to a continuous world of 3-dimensional lattices (2021). https://arxiv.org/abs/2109.11538
Edelsbrunner, H., Heiss, T., Kurlin, V., Smith, P., Wintraecken, M.: The density fingerprint of a periodic point set. In: SoCG, vol. 189, pp. 32:1–32:16 (2021)
Grünbaum, F., Moore, C.: The use of higher-order invariants in the determination of generalized Patterson cyclotomic sets. Acta Cryst. A 51, 310–323 (1995)
Kurlin, V.: A complete isometry classification of 3-dimensional lattices (2022). https://arxiv.org/abs/2201.10543
Kurlin, V.: A computable and continuous metric on isometry classes of high-dimensional periodic sequences (2022). https://arxiv.org/abs/2205.04388
Kurlin, V.: Mathematics of 2-dimensional lattices. arxiv:2201.05150 (2022)
Mosca, M., Kurlin, V.: Voronoi-based similarity distances between arbitrary crystal lattices. Cryst. Res. Technol. 55(5), 1900197 (2020)
Pozdnyakov, S., et al.: Incompleteness of atomic structure representations. Phys. Rev. Let. 125, 166001 (2020)
Ropers, J., et al.: Fast predictions of lattice energies by continuous isometry invariants. In: Proceedings of DAMDID 2021. https://arxiv.org/abs/2108.07233
Widdowson, D., Kurlin, V.: Resolving the data ambiguity for periodic crystals. Adva. Neural Inf. Proc. Syst. 35 (NeurIPS 2022). arXiv:2108.04798
Widdowson, D., et al.: Average minimum distances of periodic point sets. MATCH Commun. Math. Comput. Chem. 87, 529–559 (2022)
Zhu, Q., et al.: Analogy powered by prediction and structural invariants. J. Am. Chem. Soc. 144, 9893–9901 (2022). https://doi.org/10.1021/jacs.2c02653
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this paper
Cite this paper
Anosova, O., Kurlin, V. (2022). Density Functions of Periodic Sequences. In: Baudrier, É., Naegel, B., Krähenbühl, A., Tajine, M. (eds) Discrete Geometry and Mathematical Morphology. DGMM 2022. Lecture Notes in Computer Science, vol 13493. Springer, Cham. https://doi.org/10.1007/978-3-031-19897-7_31
Download citation
DOI: https://doi.org/10.1007/978-3-031-19897-7_31
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-19896-0
Online ISBN: 978-3-031-19897-7
eBook Packages: Computer ScienceComputer Science (R0)