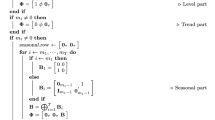Modelling and Forecasting Based on Recurrent Pseudoinverse Matrices

Abstract

Time series modelling and forecasting techniques have a wide spectrum of applications in several fields including economics, finance, engineering and computer science. Most available modelling and forecasting techniques are applicable to a specific underlying phenomenon and its properties and lack generality of application, while more general forecasting techniques require substantial computational time for training and application. Herewith, we present a general modelling framework based on a recursive Schur - complement technique, that utilizes a set of basis functions, either linear or non-linear, to form a model for a general time series. The basis functions need not be orthogonal and their number is determined adaptively based on fitting accuracy. Moreover, no assumptions are required for the input data. The coefficients for the basis functions are computed using a recursive pseudoinverse matrix, thus they can be recomputed for different input data. The case of sinusoidal basis functions is presented. Discussions around stability of the resulting model and choice of basis functions is also provided. Numerical results depicting the applicability and effectiveness of the proposed technique are given.

1 Introduction

General time series modelling and forecasting has become an essential tool in several scientific fields and business sectors, spanning from physics and engineering to workforce prediction and finance. Several methods have been proposed in the literature for modelling and forecasting time series based on either statistical or Machine Learning techniques. The most notable methods in the statistical methods class include Exponential Smoothing (ES), Auto-Regressive Integrated Moving Average (ARIMA), State Space and Structural models, Kalman filter, Nonlinear models and Generalized Auto-Regressive Conditionally Heteroscedastic (GARCH) models.

Exponential Smoothing (ES) was proposed in the1960 s by Brown, Holt and Winters [3, 11, 27], has been used extensively along with its variants due to its simplicity and adaptability to various scientific fields [14, 25]. Auto-Regressive (AR), Auto-Regressive Moving Average (ARMA) and Auto-Regressive Integrated Moving Average (ARIMA) models were first proposed by Box and Jenkins [2] in the1970 s. Estimation techniques for the parameters of such methods have been discussed in [2]. Several univariate time series forecasting variants of such models have been proposed in the literature including ARARMA [18], Vector ARIMA (VARIMA) [21, 23], Automatic univariate ARIMA type models [24] and seasonal approaches such as STL or $X-11$ [4, 5]. In the1980 s, state space models have been also used including Dynamic Linear Models (DLM) [9] and Basic Structural Models (BSM) [10] along with several variants [20]. In the quantitative finance domain Generalized Auto-Regressive Conditionally Heteroscedastic (GARCH) models [6] have been used. Nonlinear variants that handle asymmetric volatility have been also presented and studied [1, 17].

Research around non-linear modelling techniques has also been conducted however not in such extent. This is primarily because of their increased complexity and the lack of closed form formulas. In this field notable contributions include the work of Wiener [26] and others [19]. Detailed overview on the advances of time series modelling and forecasting techniques over the last decades are given in [8] and references inside. Moreover, large scale benchmarking of popular modelling and forecasting techniques are given in [15].

Despite the popularity and wide use of the aforementioned techniques, they are mostly dedicated tools tuned specifically to a use case relying on restrictive assumptions for the form and nature of the data. General models such as Artificial Neural Networks or Support Vector Machines handle those limitations but they require substantial amounts of data, increased training and retraining times, as well as substantial tuning of the large number of hyperparameters. A different approach is followed by Fast Orthogonal Search (FOS) and its variants [12, 13, 16], which can form general models using combinations of linear and non-linear basis functions. These methods are based on Gram - Schmidt and Modified Gram - Schmidt orthogonalization as well as a Cholesky type factorization approaches. These methods build the model incrementally based on a re-orthogonalization approach. The time series is projected to this orthogonal set and until a prescribed modelling error is achieved. However, inherently parallel orthogonalization procedures have instabilities and stable variants are inherently sequential, thus cannot take advantage of novel multicore architectures. Furthermore, for models composed of a large number of trigonometric components, retraining the model requires re-computation of the coefficients performed by backward - forwards substitution, which is inherently sequential.

In this article a novel inherently parallel Schur complement based pseudoinverse matrix modelling and forecasting technique is proposed. The proposed scheme is based on a recursive pseudoinverse matrix to form a model based on a predefined set of linearly independent (linear or non-linear) basis functions. Basis functions are accumulated recursively into the model until a prescribed error is achieved. The stability of the model is ensured by enforcing positive definiteness of the dot product matrix of basis functions through monitoring of error reduction as well as monitoring the magnitude of the diagonal elements. Retraining of the produced model is limited to the pseudoinverse matrix by vector product. By exploiting orthogonality features, computing the residual time series is avoided, improving computational complexity. Discussions and implementation details regarding the computation of the pseudoinverse matrix and model formation are also provided. The case of sinusoidal basis functions is also discussed along with a technique to accurately determine frequencies based on the proposed approach. The efficiency and applicability of the proposed scheme is assessed in a variety of time series with different characteristics.

In Sect. 2, the recursive Schur complement based pseudoinverse matrix of basis functions is introduced. In Sect. 3, the Schur complement based pseudoinverse matrix is utilized in the design of the proposed modelling technique in order to computed the weights of the respective basis. Discussions on the stability of the scheme and implementation details are also provided. In Sect. 4, the case of sinusoidal basis functions is examined and discussed. In Sect. 5, numerical results are presented depicting the applicability and accuracy of the proposed scheme along with discussions for several time series.

2 Recursive Schur Complement Based Pseudoinverse Matrix of Basis Functions

Let us consider a matrix composed of a set of n basis functions:

$$\begin{aligned} X= \begin{bmatrix} x_1(t)&x_2(t)&\ldots&x_n(t) \end{bmatrix}, \end{aligned}$$

(1)

where $x_i(t),1\le i \le n$ are the basis functions and t is the time variable. We can expand a general time series y based on the $x_i(t)$:

$$\begin{aligned} y=a_1 x_1(t) + a_2 x_2(t) + \ldots + a_n x_n(t) + \epsilon (t), \end{aligned}$$

(2)

where $\epsilon (t)$ is the error term and $a_i,1\le i \le n$ are the unknown coefficients that have to be determined. The Eqs. (2) can be written in block form:

$$\begin{aligned} y=Xa. \end{aligned}$$

(3)

or equivalently,

$$\begin{aligned} a=X^{+}y=(X^T X)^{-1} X^T y. \end{aligned}$$

(4)

Thus, the coefficients can be determined by solving the least squares linear system (3) or through the pseudoinverse $X^{+}$ (4). However, in many cases the basis functions are not known a priori and are computed iteratively or recurrently up to prescribed tolerance. This requires formation and solution of multiple least squares linear systems, which increases substantially the computational work. To avoid such issues modelling techniques such as Fast Orthogonal Search (FOS) and variants [12, 13, 16] have been proposed, based on Gram - Schmidt and Modified Gram - Schmidt orthogonalization as well as Cholesky factorization type approaches. These methods build the model incrementally by adding basis functions and re-orthogonalize with the already computed ones in order to project the time series and reduce the modelling error.

In order to avoid computational costs and instabilities involved in using orthogonalization procedures, while retaining the flexibility of incrementally building the model, a novel approximate inverse scheme is proposed. Let as consider the matrix $X_i$ containing up to the i-th base and an additional base F:

$$\begin{aligned} X_{i+1}= \begin{bmatrix} X_i\; |\; F \end{bmatrix} \end{aligned}$$

(5)

or:

$$\begin{aligned} K_{i+1}=X^T_{i+1} X_{i+1}= \begin{bmatrix} X^T_i X_i &{} X^T_i F\\ F^T X_i &{} F^T F \end{bmatrix} = \begin{bmatrix} K_i &{} b\\ b^T &{} d \end{bmatrix}, \end{aligned}$$

(6)

where $b=X_i^T F$ and $d=F^T F$. It should be noted that the matrix $X^T_{i+1} X_{i+1}$ is Symmetric Positive Definite and thus invertible, under the assumption that the basis function are linearly independent.

Computing the inverse of the matrix $K_{i+1}$ enables formation of the pseudoinverse $X_{i+1}^{+}$ and consequently the computation of the coefficients $a_i$ to form the model. The matrix $K_{i+1}$ can be factored to enable easier inversion and avoid the update step for the elements of the inverse of the matrix $K_{i}$, which is essential in case of non-factored inverse matrices [7]:

$$\begin{aligned} K_{i+1}= \begin{bmatrix} G^{-T}_i &{} 0\\ b^T K_{i}^{-1} &{} 1 \end{bmatrix} \begin{bmatrix} D_i &{} 0\\ 0 &{} s_i \end{bmatrix} \begin{bmatrix} G^{-1}_i &{} K_{i}^{-1} b\\ 0 &{} 1 \end{bmatrix} \end{aligned}$$

(7)

or equivalently:

$$\begin{aligned} K_{i+1}^{-1}= \begin{bmatrix} G_i &{} -K_{i}^{-1} b\\ 0 &{} 1 \end{bmatrix} \begin{bmatrix} D_i^{-1} &{} 0\\ 0 &{} s_i^{-1} \end{bmatrix} \begin{bmatrix} G^T_i &{} 0\\ -b^T K_{i}^{-1} &{} 1 \end{bmatrix}=G_{i+1} D_{i+1}^{-1} G^T_{i+1} \end{aligned}$$

(8)

where the matrix $D_i$ retains the Schur complements $s_i$ corresponding to each addition of a basis functions. The Schur complements are of the form: $s_i = d - b^T G_{i} D^{-1}_{i} G^T_{i} b$. Due to the symmetric nature of the inverse $K^{-1}_{i+1}$ only the factors $D_{i+1}$ and $G_{i+1}$ are required. Thus, we have:

$$\begin{aligned} G_{i+1}= \begin{bmatrix} G_i &{} -G_{i} D_{i}^{-1} z\\ 0 &{} 1 \end{bmatrix}\;\;and\;\; D^{-1}_{i+1}= \begin{bmatrix} D_i^{-1} &{} 0\\ 0 &{} (d-z^T D^{-1}_i z)^{-1} \end{bmatrix} \end{aligned}$$

(9)

where $z=G_i^T b$. Addition of a new basis is limited to simple “matrix times vector” operations, which can be efficiently performed in modern CPUs or accelerators such as GPUs. The storage requirements for the inverse are limited to the upper triangular matrix $G_i$, which retains $i(i+1)/2$ elements, and the diagonal matrix $D_i$ retaining i elements.

In order to avoid breakdowns in case of weak linear independence between different basis functions or loss of numerical precision, a condition on the magnitude of the diagonal element (Schur Complement) should be imposed. If the diagonal element is close to machine precision, in practice less than $\sqrt{\epsilon _{mach}}$, it is substituted with $\sqrt{\epsilon _{mach}}$, thus avoiding breakdowns.

3 Schur Based Pseudoinverse Matrix Modelling and Forecasting

The choice of basis functions for creating a model can be arbitrary, since they are evaluated and stored in the columns of matrix X. However, the amount and type of functions chosen affects the accuracy of the model and computational work. Considering the basis functions of Eq. (1), the general time - series of Eq. (2) and the recursive inverse matrix of Eq. (8) we can obtain the coefficients $a_{i}$, after the addition of the $i+1$ basis function, as follows:

$$\begin{aligned} \begin{bmatrix} a_i \\ b \end{bmatrix}= \begin{bmatrix} G_i &{} -G_{i}D_i^{-1}G^T_{i} X_i^T F\\ 0 &{} 1 \end{bmatrix} \begin{bmatrix} D_i^{-1} &{} 0\\ 0 &{} s_i^{-1} \end{bmatrix} \begin{bmatrix} G^T_i &{} 0\\ -F^T X_{i} G_{i} D_i^{-1} G^T_{i} &{} 1 \end{bmatrix} \begin{bmatrix} X_i^T y \\ F^T y \end{bmatrix} \end{aligned}$$

(10)

where $s_i = F^T F - F^T X_i G_{i}D_i^{-1}G^T_{i} X_i^T F$. The addition of a basis function involves updating of the values of already computed coefficients $a_i$ corresponding to the i basis functions. Let $g_{i+1} = -G_{i}D_i^{-1}G^T_{i} X_i^T F$ then we have:

$$\begin{aligned} a_{i+1}= \begin{bmatrix} a^*_i \\ b \end{bmatrix}= \begin{bmatrix} a_i+g_{i+1}b \\ s^{-1}_i (F^T+g^T_{i+1}X_i^T)y \end{bmatrix} \end{aligned}$$

(11)

where $a_i=G_i D^{-1}_i G^T_i X_i^T y$ and $s_i=F^T(F+X_i g_{i+1})$. The coefficients $a^*_i$ are updated after the inclusion of basis function F, while matrix $X_i$ retains all basis functions up to i-th. The residual time series update equation, with respect to the addition of a new basis function can be formed using Eq. (11) as follows:

$$\begin{aligned} \begin{bmatrix} X_i&F \end{bmatrix} a_{i+1}= \begin{bmatrix} X_i&F \end{bmatrix} \begin{bmatrix} a^*_i \\ b \end{bmatrix} \end{aligned}$$

(12)

or:

$$\begin{aligned} r_{i+1}=y- \begin{bmatrix} X_i&F \end{bmatrix} \begin{bmatrix} a^*_i \\ b \end{bmatrix} =y-X_i a^{*}_i - F b=r^*_i-F b=r_i-(X_i g_{i+1} + F)b. \end{aligned}$$

(13)

Using Eq. (13) the norm of the residual, after addition of a basis function, can be computed as follows:

$$\begin{aligned} r_{i+1}=r_i-(X_i g_{i+1} + F)b=r_i-(I-X_i G_i D_i^{-1} G_i^T X_i^T)Fb=r_i-(I-P_{X_i})Fb, \end{aligned}$$

(14)

where $P_{X_i}$ is an orthogonal projection operator onto the subspace spanned by the columns of $X_i$. The Eq. (14) implies also the following:

$$\begin{aligned} P_{X_i}r_i = 0 \;\; or \;\; r_i \perp span(X_i). \end{aligned}$$

(15)

Thus, we have:

$$\begin{aligned} \Vert r_{i+1} \Vert _2^2 = \Vert r_{i}\Vert _2^2-\Vert (X_i g_{i+1} +F)b \Vert _2^2 = \Vert r_{i}\Vert _2^2-b^2 s_i, \end{aligned}$$

(16)

or

$$\begin{aligned} \Vert r_{i+1} \Vert _2 = \sqrt{\Vert r_{i}\Vert _2^2-b^2 s_i}. \end{aligned}$$

(17)

Equation (17) can be used to assess progress of fitting, instead of computing the norm of the residual at each iteration, substantially improving performance especially in the case of increased number of basis functions. Moreover, the quantity $b^2 s$ is positive since matrix $X_i^T X_i$ is Symmetric Positive Definite, thus its Schur Complement is also Symmetric Positive Definite, leading to monotonic reduction of the norm of the residual $r_{i+1}$.

The initial conditions for Eqs. (11) and (13) are the following:

$$\begin{aligned} G_1=1 \end{aligned}$$

(18)

$$\begin{aligned} D^{-1}_1=(X_1^T X_1)^{-1} \end{aligned}$$

(19)

and

$$\begin{aligned} a_1=(X_1^T X_1)^{-1} X_1^T y. \end{aligned}$$

(20)

The procedure for computing the coefficients $a_i$ is described in the Algorithm 1. The chosen basis functions are evaluated for $t=1,...,T$ and stored in the columns of matrix $X$. Thus, the model can be formed by computing $Xa$. The formed model can be used to compute forecasts up to predefined horizon $h$. This can be achieved by initially progressing the set of basis function in time, e.g. evaluate them for $t^*=T+1,...,T+h$ and store them to the columns of a matrix $X^*=[x_1(t^*) \ldots x_n(t^*)]$. Then, the forecasts can be computed by $X^*a$. In practice, the choice of basis functions can be arbitrary, e.g. linear or non-linear or combinations.

The stability of the model with respect to each addition of a basis function can be ensured by allowing basis function to be added only if the error reduction, caused by such an addition, is positive ($b^2 s \ge 0$) and the reduction of the error does not render the error term negative $\rho <0$ ($\rho \ge b^2 s$). These conditions ensure invertibility of the matrix $X_i^T X_i$ and positive definiteness of the inverse matrix $G_i D_i ^{-1} G_i^T$, by allowing inclusion of basis functions that are suitably linearly independent to the already selected ones.

4 The Case of Sinusoidal Basis Functions

Sinusoidal basis functions can be used to form a model for general time series. In the case of strong trigonometrical phenomena in a time series, such basis functions can be used to capture them. The sinusoidal basis functions are of the following form:

$$\begin{aligned} b_i(t) = A cos(\omega _i t) + B sin(\omega _i t), \end{aligned}$$

(21)

where $\omega _i$ is the frequency. Estimation of frequencies can be performed using techniques such as the Fast Fourier Transform through the spectrum or the Quinn - Fernandes algorithm [22]. The proposed scheme allows for determining frequencies with arbitrary accuracy through frequency searching similar to the procedure described in [12]. In case of the proposed technique basis function of the form $F=cos(\omega _i t)$ followed by a basis function of the form $F=sin(\omega _i t)$ for various frequencies $\omega _i \in (0,pi]$ are fitted and the frequency that results in maximum error reduction is selected. The selected frequency becomes part of the model, is excluded from the search space, and the procedure continues until the error criterion is met. The search space $(0,pi)$ is sampled based on a prescribed sampling interval $\delta \omega$. The choice of $\delta \omega$ affects the accuracy in which the frequencies are determined. The advantages of this technique are that frequencies can be determined in parallel while the residual time series need not be computed explicitly.

In order to assess the accuracy of the technique the following example is provided. Let us consider the following:

$$\begin{aligned} y(t) = cos(\omega _1 t) + 3sin(\omega _2 t) + 2 cos(\omega _3 t) - cos(\omega _4 t) + sin(\omega _4 t) + \sigma (t) \end{aligned}$$

(22)

where $\sigma (t)$ is following uniform random distribution with average equal to $0.5$. The frequencies $\omega _i$ are: $\omega _1 = 0.0546$, $\omega _2 = 0.83120$, $\omega _3 =1.87120$ and $\omega _4 = 1.91320$. The frequencies are estimated using Fast Fourier Transform (FFT), Quinn - Fernandes method based on FFT as initial guess coupled with Ordinary Least Squares (OLS) method and the proposed technique. The results are given in Table 1.

Table 1. Percentage errors for frequency estimation.

The choice of $\delta \omega$, in the proposed scheme, should be less than the sampling interval of the Fast Fourier Transform, e.g. $\delta \omega \le \frac{2*pi}{N}{}$, in order to allow accurate determination of the frequencies and avoid undersampling.

The proposed technique can be used to estimate the frequency to improved accuracy compared to FFT or the QF-OLS method. The proposed scheme can be coupled also with either the FFT or QF-OLS method and hybrid schemes can be designed leveraging the advantages of those schemes. This will be studied in future work.

5 Numerical Results

In this section the applicability and accuracy of the proposed scheme is examined by applying the proposed technique to three time series. The two error measures used to assess the forecasting error was Mean Absolute Percentage Error (MAPE) and Mean Absolute Deviation (MAD):

$$\begin{aligned} MAPE = \frac{100}{T} \sum _{i=1}^{T} \frac{|y_i - \hat{y}_i |}{|y_i|} \text { and } MAD=\frac{1}{T}\sum _{i=1}^{T} |y_i - \hat{y}_i|, \end{aligned}$$

(23)

where $y_i$ are the actual values, $\hat{y}_i$ the forecasted values and $T$ the length of the test set. The basis functions chosen to model the selected time series were:

$$\begin{aligned} F_1 = 1, F_2 = t, F_3 = e^t, F_i = A cos(\omega _i t) + B sin(\omega _i t), i \ge 4, t \ge 0. \end{aligned}$$

(24)

The linear and exponential basis were added to automatically capture such trends in the data. It should be mentioned that the time variable $t$ is scaled for the linear and exponential components to improve numerical behavior during inversion of the matrix of basis functions.

5.1 US Airline Passenger Volume

This US airline passenger volume dataset was extracted from R Studio and is composed of monthly total volumes of passengers spanning from January 1949 to December 1960 (144 samples). The training part was composed of $75\%$ of the dataset, while the test part was composed of $25\%$ of the dataset, specifically the training part included $108$ samples and the test part included $36$ samples, as presented in Fig. 1. The prescribed interval $\delta \omega$ for frequency search was set to $0.001$ and the prescribed tolerance for fitting the model was set to $\epsilon =0.01$. The forecasted values along with the actuals are given in Fig. 2. The MAPE and MAD of the forecasts were $9.3474$ and $40.0410$, respectively. From Fig. 2 we observe that the proposed scheme captured the exponential and linear tendency automatically as well as the underlying trigonometric phenomena, without requiring any pre-processing steps for the input data apart from maximum scaling.

Fig. 1.

Train and test parts for the US airline passenger volume dataset.

Fig. 2.

Forecasted and actual values for the US airline passenger volume dataset.

With respect to the value of the coefficients comprising the model the time series exhibits a significant exponential component, a weak linear component along with a strong low frequency harmonic component, because of the yearly periodicity of the time series.

5.2 Monthly Expenditure on Eating Out in Australia

The monthly expenditure on eating out in Australia dataset was extracted from R Studio and is composed of the monthly expenditure on cafes, restaurants and takeaway food services in Australia in billion dollars. The dataset is composed of 426 samples spanning a period from April 1982 to September 2017. The training part was composed of $\approx 80\%{ ofthedatasetwhilethetestpartwascomposedof}\approx 20\%{ ofthedataset},\,{ specificallythetrainingpartincluded}342{ samplesandthetestpartincluded}84$ samples, as presented in Fig. 3. The prescribed interval $\delta \omega { forfrequencysearchwassetto}0.001{ andtheprescribedtoleranceforfittingthemodelwassetto}\epsilon =0.01$. The forecasted values along with the actuals are given in Fig. 4. The MAPE and MAD of the forecasts were 4.5292 and 0.1465, respectively.

Fig. 3.

Train and test parts for the monthly expenditure on eating out in Australia dataset.

Fig. 4.

Forecasted and actual values for the US airline passenger volume dataset.

With respect to the value of the coefficients comprising the model the time series exhibits a strong exponential component, a strong linear component along with a relatively significant medium frequency harmonic components.

5.3 Call Volume for a Large North American Bank

The call volume for a large North American bank dataset was extracted from R Studio and is composed of the volume of calls, per five minute intervals, spanning 164 d starting from 3 March 2003. The dataset is composed of 27716 samples. The training part was composed of $\approx 80\%{ ofthedatasetwhilethetestpartwascomposedof}\approx 20\%$ of the dataset, specifically the training part included 22325 samples and the test part included 5391 samples, as presented in Fig. 5. The prescribed interval $\delta \omega { forfrequencysearchwassetto}10^{-5}{} { andtheprescribedtoleranceforfittingthemodelwassetto}\epsilon =0.088.{ Thevalueofthetolerance}\epsilon$ is chosen as below that margin the rate of error reduction slows down significantly due to the presence of noise in the form of a large number of frequencies with the same magnitude in the spectrum. This issue can be overcome by increasing the samples of the spectrum, however this substantially increases the computational work, without significant improvement in the forecasting error. The forecasted values along with the actuals are given in Fig. 6. The MAPE and MAD of for the forecasts were 15.1580 and 25.4576, respectively.

Fig. 5.

Train and test parts for the call volume for a large North American bank dataset.

Fig. 6.

Forecasted and actual values for call volume for a large North American bank dataset.

With respect to the value of the coefficients the model has a weak exponential component that is counteracted by a weak linear component. There are also strong low frequency components that contribute significantly in the reduction of the error.

5.4 Discussions

The proposed scheme was able to capture the dominant characteristics of the different time series. The choice of the basis functions substantially affects the estimation and the forecasting error. For example, for the model problem of Subsection 5.3 the linear and exponential basis do not contribute significantly to the accuracy of the model, while also increasing the computational complexity since the dimensions of the pseudoinverse matrix grow. However, to preserve generality and wide applicability, a common set of basis functions was retained for all experiments.

Another important issue is the estimation of frequencies, which for the low value of the $\delta \omega$ parameter requires substantial computational work especially in the case of large training data. In order to reduce computational complexity, frequency estimation can be performed by means of either FFT or the Quinn - Fernandes algorithm [22] or hybrid approaches which will be studied in future research.

The generality of the approach allows the incorporation of basis functions based on nonlinear modelling techniques such as Artificial Neural Networks (ANN) and Support Vector Machines (SVM) trained by subsets of the available dataset. The effect of such basis functions will be studied also in future research.

6 Conclusion

A novel Schur complement based pseudoinverse matrix approach for modelling and forecasting general time series has been proposed. The proposed technique can incorporate linear and non-linear components during model formation, thus avoiding preprocessing and transformation of the time series or restrictive assumptions related to the statistical properties of the data. Stability of the model is ensured by enforcing positive definiteness of the dot product matrix of basis functions $(X^T X)$ and its inverse, and monotonic reduction of the error. A frequency detection technique is also presented based on the proposed scheme. The proposed scheme does not require preprosessing of time series and is assessed by modelling several time series exhibiting combinations of exponential, linear, trigonometric and random characteristics. Moreover, the model relies on a single parameter and it is suitable for modelling general time series.

Future work is directed towards the design of a parallel approximate pseudoinverse matrix approach in order to reduce storage requirements especially in the case of large number of basis functions. Moreover, an adaptive approach for frequency estimation is under further research.