1 Introduction

Neural networks (NN), in particular deep neural networks, promise astounding advances across a manifold of computing applications across domains as diverse as image classification [27], natural language processing [21], and game playing [40]. NNs are the technical core of ever more intelligent systems, created to assist or replace humans in decision-making.

This development comes with the urgent need to devise methods to analyze, and ideally verify, desirable behavioral properties of such systems. Unlike for traditional programming methods, this endeavor is hampered by the nature of neural networks, whose complex function representation is not suited to human inspection and is highly resistant to mechanical analysis of important properties.

Verification Challenge. As a matter of fact, remarkable progress is being made towards automated NN analysis, be it through specialized reasoning methods of the SAT-modulo-theories family [10, 23, 25], or through suitable variants of abstract interpretation [13, 31] or quantitative analysis [7, 42]. All these works thus far focus on the verification of individual NN decision episodes, i.e., the behavior of a single input/output function call. In contrast, the verification of NNs being the decisive (in the literal sense of the word) authorities inside larger systems placed in possibly uncertain contexts, is wide-open scientific territory.

Very many real-world examples, where NNs are expected to become central decision entities – from autonomous driving to medical care robotics – involve discrete decision making in the presence of random phenomena. The former are to be taken in the best possible manner, and it is the NN that decides which decisions to take when and where. A very natural formal model for studying the principles, requirements, efficacy and robustness of such a NN, is the model family of Markov decision processes [38] (MDP). MDPs are a very widely studied class of models in the AI community, as well as in the verification community, where MDPs are the main semantic object of probabilistic model checking [29].

Assume now we are facing a problem for which a NN decision entity has been developed by a different party. If the problem statement can be formally cast as a certain MDP, we may use this MDP as a context to study properties of the NN delivered to us. Concretely, the NN will be put to use as a determinizer of the otherwise non-deterministic choices in the MDP, so that altogether a Markov chain results, which in turn can be evaluated by standard probabilistic model checking techniques. This is the simple idea this paper proposes. The idea can be further extended by making the technology available to a certification authority responsible for NN system approval, or to the party designing the NN, as a valuable feedback mechanism in the design process.

Deep Statistical Model Checking. However, this style of verification is challenged by the complexity of analyzing the participating NN and that of analyzing the induced system behaviors and interactions. Already the latter is a notorious practical impediment to successful verification rooted in state space explosion problems. Indeed, standard probabilistic model checking will suffer quickly from this. However, for Markov chains there is a scalable alternative to standard model checking at hand, nowadays referred to as statistical model checking [20, 43]. The latter method employs efficient sampling techniques to statistically check the validity of a certain formal property. If applicable, it does not suffer from the state space explosion problem, in contrast to standard probabilistic model checking.

The scalable verification method we propose is called deep statistical model checking (DSMC) by us. At its core is a straightforward variation of statistical model checking, applied to a MDP, together with a NN that has to take the decisions. For this, DSMC expects a NN that can be queried as a black-box oracle to resolve the non-determinism in the MDP given: The NN receives the state descriptor as input, and it returns as output a decision determining the next step. The DSMC method integrates the pair of NN and MDP, and analyzes the resulting Markov chain statistically. In this way, it is possible to statistically verify properties of the NN itself, as we will discuss.

Racetrack. To study the potential of DSMC, we perform practical experiments with a case study family that remotely resembles the autonomous driving challenge, albeit with some drastic restrictions relative to the grand vision. These restrictions are: (i) We consider a single vehicle, there is no traffic otherwise. (ii) No object or position sensing is in use, instead the vehicle is aware of its exact position and speed. (iii) No speed limits or other traffic regulations are in place. (iv) Fuel consumption is not optimized for. (vi) Weather and road conditions are constant. (vii) The entire problem is discretized in a coarse manner. What remains after all these restrictions (apart from inducing a roadmap of further works beyond what we study) is the problem of navigating a vehicle from start to goal on a discrete map, with actions allowing to accelerate/decelerate in discrete directions, subject to a probabilistic risk of action failing to take effect in each step. The objective is to reach the goal in a minimal number of steps without bumping into a boundary wall. This problem is known as the Racetrack, a benchmark originating in AI autonomous decision making [1, 37]. In formal terms, each map and parameter combination induces a MDP.

Racetrack is a simple problem, simple enough to put a neural network in the driver seat: This NN is then the central authority in the vehicle control loop. It needs to take action decisions with the objective to navigate the vehicle safely towards the goal. There are a good number of scientific proposals on how to construct and train a NN for mastering such tasks, and the present paper is not trying at all to innovate in this respect. Instead, the central contribution of this paper is a scalable method to verify the effectiveness of a NN trained externally for its task. This technique, DSMC, is by no means bound to the Racetrack problem domain, instead it is generally applicable. We evaluate it in the context of Racetrack because we do think that this is a crisp formal model family, which is of value in ongoing activities to systematize our understanding of NNs that are supposed to take over important decisions from humans.

Our concrete modelling context are MDPs represented in Jani  [6], a language interfacing with the leading probabilistic model checkers out there. For the sake of experimentation and for use by third parties, we have implemented a generic connection between NNs and the state-of-the-art statistical model checker modes [2, 5], part of The Modest Toolset  [18]. This extension gives the possibility to use a NN oracle, and to analyze the resulting Markov chain by SMC. We thus establish an initial DSMC tool infrastructure, which we apply on Racetrack benchmarks.

It will become evident by our empirical evaluation that there are a variety of use cases for DSMC, pertaining to end users and domain engineers alike:

  • Quality Assurance. DSMC can be a tool for end users, or engineers, in system approval or certification, regarding safety, robustness, absence of deadlocks, or performance metrics. The generic connection to model checking furthermore enables the comparison of NN oracles to provably optimal choices, on moderate-size models: taking out the NN, the original MDP results, and can be submitted to standard probabilistic model checking. In our implementation, we use mcsta [18] for this purpose.

  • Learning Pipeline Assessment. DSMC can serve as a tool for the NN engineers designing the NN learning pipeline in the first place. This is because the DSMC analysis can reveal specific deficiencies in that pipeline. For example, we show that simple heat maps can highlight where the oracles are unsafe. And we exhibit cases where NN oracles turn out highly unsafe despite this phenomenon not being derivable from standard measures of learning performance. Such problems would likely have remained undetected without DSMC.

In summary, our contributions are as follows:

  1. 1.

    We present deep statistical model checking, which statistically evaluated the connection of a NN oracle and a MDP formalizing the problem context.

  2. 2.

    We establish tool infrastructure for DSMC within modes to connect to NN oracles.

  3. 3.

    We establish infrastructure for Racetrack benchmarking, including parsing, simulation, Jani model export, comparison with optimal behavior, and also for NN learning.

  4. 4.

    We illustrate the use and feasibility of DSMC in Racetrack case studies.

The benchmark and all infrastructure including our modification of modes as well as our Jani model is archived and publicly available at DOI 10.5281/zenodo.3760098 [14].

The paper is organized as follows. Section 2 briefly covers the necessary background in model checking, neural networks, and the Racetrack benchmark. Section 3 introduces the DSMC connection and discusses our implementation. Section 4 briefly introduces our Racetrack infrastructure, specifically the Jani model and the NN learning machinery. Section 5 describes the case studies, and Sect. 6 closes the paper.

2 Background

Markov Decision Processes. The models we consider are discrete-state Markov Decision Processes (MDP). For any nonempty set S we let \(\mathcal {D}(S)\) denote the set of probability distribution over S. We write \(\delta (s)\) for the Dirac distribution that assigns probability 1 to \(s\in S\).

Definition 1 (Markov Decision Process)

A Markov Decision Process (MDP) is a tuple \(\mathcal M= \langle \mathcal S, \mathcal A, \mathcal T, s_0\rangle \) consisting of a finite set of states \(\mathcal S\), a finite set of actions \(\mathcal A\), a partial transition probability function \(\mathcal T:\mathcal S\times \mathcal A\nrightarrow \mathcal {D}(\mathcal S)\), and an initial state \(s_0\in \mathcal S\). We say that action \(a \in \mathcal A\) is applicable in state \(s \in \mathcal S\) if \(\mathcal T(s,a)\) is defined. We denote by \(\mathcal A(s) \subseteq \mathcal A\) the set of actions applicable in s. We assume that \(\mathcal A(s)\) is nonempty for each s (which is no restriction).

MDPs are often associated with a reward structure, specifying numerical rewards to be accumulated when moving along states sequences. Here we are interested instead in the probability of property satisfaction. Rewards, however, appear in our case study as part of the NN training which aims at optimizing reward expectations during reinforcement learning.

The behavior of a MDP is usually considered together with an entity resolving the otherwise non-deterministic choices in a state. This is effectuated by an action policy (or scheduler, or adversary) that determines which applicable action to apply when and where. In full generality this policy may use randomization (picking a distribution over applicable actions), and it may use the past history when picking. The former is of no importance for the setting considered here, while the latter is. Histories are represented as finite sequences of states (i.e. words over \(\mathcal S\)), thus they are drawn from \(\mathcal S^+\). We use \(\textit{last}(w)\) to denote the last state in \(w \in \mathcal S^+\).

Definition 2 (Action Policy)

A (deterministic, history-dependent) action policy is a function \(\sigma :\mathcal S^+ \rightarrow \mathcal A\) such that \(\forall w \in \mathcal S^+ :\sigma (w) \in \mathcal A(\textit{last}(w))\). An action policy is memoryless if it satisfies \(\sigma (w)=\sigma (w')\) whenever \(\textit{last}(w) = \textit{last}(w')\).

Memoryless policies can equally be represented as \(\sigma :\mathcal S\rightarrow \mathcal A\) such that \(\forall s \in \mathcal S:\sigma (s) \in \mathcal A(s)\).

Definition 3 (Markov Chain)

A Markov Chain is a tuple \(\mathcal C= \langle \mathcal S, \mathcal T, s_0\rangle \) consisting of a set of states \(\mathcal S\), a transition probability function \(\mathcal T:\mathcal S\rightarrow \mathcal {D}(\mathcal S)~\) and an initial state \(s_0\in \mathcal S\).

An MDP \(\langle \mathcal S, \mathcal A, \mathcal T, s_0\rangle \) together with an action policy \(\sigma :\mathcal S^+ \rightarrow \mathcal A\) induces a countable-state Markov chain \(\langle \mathcal S^+, \mathcal T', s_0\rangle \) over state histories in the obvious way: For any \(w\in S^+\) with \(\mathcal T(\textit{last}(w),\sigma (w))=\mu \), set \(\mathcal T'(w)=d\) where \(d(ws)=\mu (s)\). For memoryless \(\sigma \) the original state space \(\mathcal S\) can be recovered by setting \(\mathcal T'(\textit{last}(w))=\mu \) in the above, since both are lumping equivalent [4].

Probabilistic and Statistical Model Checking. Model checking of probabilistic models (such as MDPs) nowadays comes in two flavors. Probabilistic model checking (PMC) [29] is an algorithmic technique to determine the extremal (maximal or minimal) probability (or expectation) with which an MDP satisfies a certain (temporal logic) property when ranging over all imaginable action policies. For some types of properties (step-bounded reachability, expected number of steps to reach) it does not suffice to restrict to memoryless policies, while for others (inevitability, step-unbounded reachability) it does. At the core of PMC are numerical algorithms that require the full state space to be available upfront (in some way or another) [17, 35].

If fixing a particular policy, the MDP turns into a Markov chain. In this setting, statistical model checking (SMC [20, 43]) is a popular alternative to probabilistic model checking. This is because PMC, requiring the full state space, is limited by the state space explosion problem. SMC is not, even if the underlying model is infinite in size. Furthermore, SMC can extend to non-Markovian formalisms or complex continuous dynamics effectively. At its core, SMC harvests classical Monte Carlo simulation and hypothesis testing techniques. In a nutshell, n finite samples of model executions are generated and evaluated to determine the fraction of executions satisfying a property under study. This yields an estimate \(q'\) of the actual value q of the property, together with a statistical statement on the potential error. A typical guarantee is that \(\mathbb {P}(|q'-q|<\epsilon ) > \delta \), where \(1-\delta \) is the confidence that the result is \(\epsilon \)-correct. To decrease \(\epsilon \) and \(\delta \), n must be increased. SMC is attractive as it only requires constant memory independent of the size of the state space. When facing rare events, however, the number of samples needed to achieve sufficient confidence may explode.

In the MDP setting (or more complicated settings), SMC analysis is always bound to a particular action policy turning an otherwise non-deterministic model into a stochastic process. Nevertheless, many SMC tools support non-deterministic models, e.g. Prism  [28] and UPPAAL SMC [8]. They use an implicitly defined uniform random action policy to resolve choices. The statistical model checker modes [5], which is part of The Modest Toolset [18] instead lets the user choose out of a small set of predefined policies, or provides light-weight support for iterating over policies [5, 30] to statistically approximate an optimal policy. In any case, results obtained by SMC are to be interpreted relative to the implicitly or explicitly defined action policy.

Neural Networks. NNs consist of neurons: atomic computational units that typically apply a non-linear function, their activation function, to a weighted sum of their inputs [39]. For example, rectified linear units (ReLu) use the activation function \(f(x) = \max (0,x)\). Here we consider feed-forward NNs, a classical architecture where neurons are arranged in a sequence of layers. Inputs are provided to the first (input) layer, and the computation results are propagated through the layers in sequence until reaching the final (output) layer. In every layer, every neuron receives as inputs the outputs of all neurons in the previous layer. For a given set of possible inputs \(\mathcal {I}\) and (final layer) outputs \(\mathcal {O}\), a neural network can be considered as an efficient-to-query total function \(\pi :\mathcal {I}\rightarrow \mathcal {O}\).

So-called “deep” neural networks consist of many layers. In tasks such as image recognition, successful NN architectures have become quite sophisticated, involving e.g. convolution and max-pooling layers [27]. Feed-forward NNs are comparatively simple, yet they are in wide-spread use [12], and are in principle able to approximate any function to any desired degree of accuracy [22].

Such NNs can be trained in a multitude of ways. Here we use deep Q-learning [33], a successful and nowadays widespread form of reinforcement learning, where the NN is trained by iterative execution and refinement steps. Each step executes the current NN from some state, and updates the NN weights using gradient descent. Deep Q-learning has been shown to learn high-quality NN action policies in a variety of challenging decision-making problems [33].

Racetrack. Originally Racetrack is a pen and paper game [11]. A track is drawn with a start line and a goal line. A vehicle starts with velocity 0 from some positions on the start line, with the objective to reach the goal as fast as possible without crashing into a wall. Nine possible actions modify the current velocity vector by one unit (up, down, left, right, four diagonals, keep current velocity). This simple game lends itself naturally as a benchmark for sequential decision making in risky scenarios. In particular, extending the problem with noise, we obtain MDPs that do not necessarily allow the vehicle to reach the goal with certainty. In a variety of such noisy forms, Racetrack was adopted as a benchmark for MDP algorithms in the AI community [1, 3, 32, 36, 37].

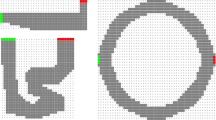
Like in previous work, we consider the single-agent version of the game. We use some of the benchmarks, i.e., track shapes, that are readily available. Specifically, we use the three Racetrack maps illustrated in Fig. 1, originally introduced by Barto et al. [1]. The track itself is defined as a two-dimensional grid, where each cell of the grid can represent a possible starting position “s” (indicated in green), a goal position “g” (red), or can contain a wall “x” (white, crossed). Like Barto et al. [1], we consider a noisy version of Racetrack that emulates slippery road conditions: actions may fail with a given probability, in which case the action does not change the velocity and the vehicle instead continues driving with unchanged velocity vector.

Fig. 1.
figure 1

The maps of our Racetrack benchmarks: Barto-small (left top), Barto-big (left bottom), Ring (right). (Color figure online)

Full size image

3 Neural Networks as MDP Action Policies

Connecting MDP and Action Oracle. Racetrack is a simple instance of many further examples representing real-world phenomena that involve randomness and decision making. This is the natural scenario where NNs are taking over ever more duties. In essence, their role is very close to that of an action policy: Decide in each situation what options to pick next. If we consider the “situations” (the inputs \(\mathcal {I}\)) as the states \(\mathcal S\) of a given MDP, and the “options” (outputs \(\mathcal {O}\)) as actions \(\mathcal A\), then the NN is a function \(\pi :\mathcal S\rightarrow \mathcal A\). We call such a function an action oracle. Indeed this is what the reinforcement learning process in Q-learning and other approaches delivers naturally.

Observe that an action oracle can be cast into an action policy except for a subtle problem. Action policies only pick actions (from \(\mathcal A(s)\), thus) applicable at the current state s, while action oracles may not. A better fitting definition would constrain oracles to always return an applicable action. Yet it is not clear how to guarantee this for NNs – it is easy to see that, even for linear multi-classification, the hard constraints required to guarantee action applicability lead to non-convex optimization problems. An easy fix would use the highest-ranked applicable action instead of the NN classifier output itself. For our purposes however, where we want to analyze the quality of the NN oracle, it makes sense to explicitly distinguish inapplicable actions as a form of low quality.

If an oracle returns an inapplicable action, then no valid behavior is prescribed and in that sense the system can be considered stalled.

Definition 4 (Action Oracle Stalling)

Let \(\mathcal M= \langle \mathcal S, \mathcal A, \mathcal T, s_0\rangle \) be an MDP, and \(\pi :\mathcal S\mapsto \mathcal A\) be an action oracle. We say that \(s \in \mathcal S\) is stalled under \(\pi \) if \(\pi (s) \notin \mathcal A(s)\).

To accommodate for stalling, we augment the MDP upfront with a fresh action \(\dagger \) available at every state, this action is chosen upon stalling, leading to a fresh state \(\ddagger \) with only that action to continue. So \(\mathcal M= \langle \mathcal S, \mathcal A, \mathcal T, s_0\rangle \) is transformed into \(\mathcal M^\ddagger = \langle \mathcal S\cup \{\ddagger \}, \mathcal A\cup \{\dagger \}, \mathcal T', s_0\rangle \) where for each state s, \(\mathcal T' (s,\dagger )= \delta (\ddagger )\) and otherwise \(\mathcal T' (s,a) = \mathcal T(s,a)\) wherever the latter is defined.

Definition 5 (Oracle Induced Markov Chain)

Let \(\mathcal M= \langle \mathcal S, \mathcal A, \mathcal T, s_0\rangle \) be an MDP, and let \(\pi \) be an action oracle for \(\mathcal M\). Then the Markov chain \(\mathcal C^\pi \) induced by \(\pi \) is the one induced in \(\mathcal M^\ddagger \) by the memoryless action policy \(\sigma \) defined by \(\sigma (w)=\dagger \) whenever \(\textit{last}(w)\) is \(\ddagger \) or stalled under \(\pi \), and otherwise by \(\sigma (w)=\pi (\textit{last}(w))\).

In words, the oracle induced policy fixes the probability distribution over transitions in each state to that of the chosen action. If that action is inapplicable, then the chain transitions to the fresh state \(\ddagger \) which represents stalled situations.

Deep Statistical Model Checking. Overall, \(\mathcal C^\pi \) is a Markov chain that uses \(\pi \) as an oracle to determinize the MDP \(\mathcal M\) whenever possible, and stalls otherwise. With \(\pi \) implemented by a neural network, we can use statistical model checking on \(\mathcal C^\pi \) to analyze the NN behavior in the context of \(\mathcal M\). This analysis has the potential to deliver deep insights into the effectiveness of the NN applied, allowing for comparisons with other policies and also with optimal policies, the latter obtained from exhaustive model checking. From a practical perspective, an important remark is that in the definitions above and in our implementation of DSMC described below, the inputs to the NN are assumed to be the MDP states \(\mathcal S\). This captures the scenario where the NN takes the role of a classical system controller, whose inputs are system state attributes, such as program variables. More generally, the connection from the MDP model to the NN input may require an intermediate function f mapping \(\mathcal S\) to the input domain of the NN. This is in particular the case for NNs processing image sequences, like in vision systems in autonomous driving. In such a scenario, the MDP model states have to represent the relevant aspects of the NN input (e.g. objects and their properties in an image). This advanced form of connection remains a topic for future work. It lacks the crisp nature of the problem considered here.

DSMC Implementation. Deep statistical model checking is based on a pair of NN and MDP operating on the same state space. The NN is assumed to be trained externally prior to the analysis, in which it is combined with the MDP. To experiment with this concept in a real environment, we have developed a DSMC implementation inside The Modest Toolset [18], which includes the explicit-state model checker mcsta, and in particular the statistical model checker modes  [5]. modes thus far offers the options Uniform and Strict to resolve non-determinism. We implemented a novel option called Oracle, which calls an external procedure to resolve non-determinism. With that option in place, every time the next action has to be chosen, modes provides the current model state s to the Oracle, which then calls the external procedure and returns the chosen action to modes. In this way, the Oracle can connect to an external NN serving as an action oracle from modes ’s perspective.

At the implementation level, connecting to standard NN tools is non-trivial due to the programming languages used. The Modest Toolset is implemented in C#, whereas standard NN tools are bound to languages like Python or Java. Our key observation to overcome this issue is that a seamless integration is not actually required. Standard NN tools are primarily required for NN training, which is computationally intensive and requires highly optimized code. In contrast, implementing our NN Oracle requires only NN evaluation (calling the NN on a given input) which is easy – it merely requires to propagate the input values through the network. We thus implemented NN evaluation directly in The Modest Toolset ’s code base, as part of our extension. The NNs are learned using standard NN tools. From there, we export a file containing the NN weights and biases. Our extension of modes reads that file, and uses it to reconstruct the same NN, for use with our evaluation procedure. When the Oracle is called, it connects to that procedure.

modes contains simulation algorithms specifically tailored to MDP and more advanced models. The tool is implemented in C#. It offers multiple statistical methods including confidence intervals, Okamoto bound [34], and SPRT [41]. As simulation is easily and efficiently parallelizable, modes can exploit multi-core architectures.

4 Getting Concrete: The Racetrack Case Study

As previously outlined, we consider Racetrack as a simple and discrete, yet highly extensible approximation of real-world phenomena that involve randomness and decision making. In this section we spell out how these benchmarks are made concrete use of.

The Jani  framework. Central to our practical work is the Jani -model format [6, 24]. It can express models of distributed and concurrent systems in the form of networks of automata, and supports property specification based on probabilistic computation tree logic (PCTL) [16]. In full generality, Jani models are networks of stochastic timed automata, but we concentrate on MDPs here. Automatic translations from and into other modeling languages are available, connecting among others to the planning language PPDDL [26] and to the Prism language, and thus to the model checker Prism  [28]. A large set of quantitative verification benchmarks (QVBS) [19] is available in Jani, and many tools offer direct support, among them ePMC, Storm and The Modest Toolset [9, 15, 18].

Racetrack Model. For lack of space, the details of the Racetrack encoding in Jani are part of the archive publicly available at [14]. The track itself is represented as a (constant) two-dimensional array whose size equals that of the grid. The Jani files of different Racetrack instances differ only in this array. Vehicle movements and collision checks are represented by separate automata that synchronize using shared actions.

The vehicle automaton keeps track of the current vehicle state via four bounded integer variables (position and directional velocity), and two Boolean variables (indicating whether the vehicle has crashed or reached a goal). The initial automaton location has edges for each of the 9 different acceleration vectors. Each of them updates the velocity accordingly, and sends the current source and next target coordinates to the collision check automaton. It then awaits that automaton to respond with one of three answers: “valid”, “crash”, or “goal”. For the latter two, the automaton moves to a terminal location. For “valid”, the vehicle automaton sets the target coordinates as its new source coordinates and moves back to its initial location.

The collision check automaton checks whether the vehicle’s next target coordinates lie within the grid. If so, it iterates over the cells on the discretized trajectory from current source to next target, and looks up for each such cell whether it represents a wall or goal cell. Such a result is sent to the vehicle automaton as soon as available. If the entire trajectory is found free of such events, the vehicle automaton’s request is answered with “valid”, and the automaton location is reset, waiting for the next trajectory to check.

Learning Neural Networks for Racetrack. For the sake of realistic empirical studies, we have drawn on established NN learning techniques to obtain NN oracles for the Racetrack case studies. Here we briefly summarize the main design decisions. Notably, DSMC is entirely independent of the concrete learning process, depth, and shape of the NN employed.

  • NNs are learnt for a specific map (cf. Fig. 1), with the inputs being 15 integer values, encoding the two-dimensional position, the two-dimensional velocity, the distance to the nearest wall in eight directions, the x and y differences to the goal coordinates, and Manhattan goal distance (absolute x- and y-difference, summed up). Actions are encoded as classification outputs.

  • A crucial design decision is the learning objective, i.e., the rewards used in deep Q-learning. We set the reward for reaching the goal line to 100, and for crashing into a wall to \(-50\). We used a discount factor of 0.99 to encourage short trajectories to the goal. This arrangement was chosen because, empirically, it resulted in an effective learning process. With higher negative rewards for crashing, the policies learn to prefer not to move or to move in circles. Similarly, smaller negative rewards make the learnt policies prefer to crash quickly. Using a discount factor yields better learning performance, but does not match the overall Racetrack setup. This exemplifies that the choice of objectives for learning is governed by learning performance. Both meta-parameters and numeric parameters such as rewards typically require fine-tuning orthogonal to, or at least below the level of abstraction of, the qualities of interest in the application.

  • We experimented with a range of NN architectures and hyperparameter settings, the objective being to keep the NNs simple while still able to learn useful oracles in our Racetrack benchmarks. The NNs we settled on have the above described input and output layers, and two hidden layers each of size 64. All neurons use the ReLU activation function.

  • NNs are learnt in two variants: (a) starting on the starting line vs. (b) starting from a random point anywhere on the map, each with initial velocity 0. Variant (b) turned out to yield much more effective and robust learning. Intuitively, with (a) it takes the policy a long time to reach the goal at all, while with (b) this happens more quickly yielding earlier and more robust learning also farther away from the goal.

Fig. 2.
figure 2

Heat maps of NN induced crash probabilities for all Racetrack benchmarks. (Color figure online)

Full size image

5 Getting Practical: DSMC Case Studies in Racetrack

We now demonstrate the statistical model checking approach to NN policy verification through case studies in Racetrack. Section 5.1 illustrates the use of DSMC for quality assurance by human analysts (end users, engineers) in system approval. Section 5.2 illustrates the use of DSMC as a tool for the engineers designing the NN learning pipeline. Section 5.3 evaluates the computational effort incurred by DSMC compared to a conventional SMC setting where the MDP policy is coded in the model itself.

Throughout, we use modes with an error bound \(P( error > \epsilon ) < \kappa \), where \(\epsilon = 0.01\) and \(\kappa = 0.05\), i.e., a confidence of \(95\%\). We set the maximal run length to 10000 steps. Unless otherwise stated, we set the slippery-noise level in Racetrack, i.e. the probability of action failure, to \(20\%\). The NN oracles are learnt by training runs starting anywhere on the map; we will illustrate how DSMC can highlight the deficiencies of the alternate approach (starting on the starting line only). All experiments were run on an Intel(R) Core(TM) i7-4790 CPU @ 3.60 GHz (4 cores, 8 threads) with 32 GB RAM and a 450 GB HDD.

Fig. 3.
figure 3

Goal probability of NN oracle on the Barto-big benchmark trained and executed with \(20\%\) noise vs. stress-test executed with \(50\%\) noise using the same NN (middle) vs. optimal policies obtained by probabilistic model checking with \(50\%\) noise (right). (Color figure online)

Full size image

5.1 Quality Assurance in System Approval

The variety in abstract property specification gives versatility to the quality assurance process. This is important in particular because, as previously argued, the relevant quality properties will typically not be identical to the objectives used for NN learning. In the Racetrack example, NN learning optimizes expected reward subject to fine-tuned reward and discount values. For the quality assurance, we consider crash probability and goal probability, expressed as CTL path formulas in Jani, namely \(\Diamond ~\textit{crashed}\) (“eventually crashed”) for the former and \(\lnot \textit{crashed } \,\texttt {U} \, \textit{goal}\) (“not crashed until reaching goal”) for the latter.Footnote 1

We highlight that the DSMC analysis can not only point out that a NN oracle has deficiencies, but also where: in which regions of the MDP state space \(\mathcal S\). Namely, in cyber-physical systems, it is natural to use the spatial dimension underlying \(\mathcal S\) for systematizing the analysis and visualizing its result. This delivers not only a yes/no answer, but an actual quality report. We illustrate this here through the use of simple heat maps over the Racetrack road map.

Figure 2 shows quality assurance results for crash probability in all the Racetrack benchmarks, using for each the best NN oracle from reinforcement learning (i.e. those yielding highest rewards). The heat maps use a simple color scheme as an illustration how the analysis results can be visualized for the human analysts. Similar color schemes will be used in all plots below.

From the displayed DSMC results, quality assurance analysts can directly conclude that the NN oracles are fairly safe in Barto-small (left top), with crash probabilities mostly below 0.1; but not on Barto-large (left bottom) and Ring (right) where crash probabilities are above 0.5 on significant parts of the map. Generally, crash probability increases with distance to the goal line. Some interesting subtleties are also visible, for example that crash probabilities are relatively high in the left-turn before the goal in Barto-small.

Fig. 4.
figure 4

Goal probabilities on the Barto-big benchmark (color coding as in Fig. 3), for NN oracles learnt over \(n=70000\) (left) and \(n=90000\) (middle) training episodes, together with Q-learning curve (right). (Color figure online)

Full size image

Our next results, in Fig. 3, illustrate the quality-assurance versatility afforded by DSMC, through an analysis quite different from the previous one. The human analysts here decide to evaluate goal probability (a quality stronger than not crashing because the latter may be achieved by idling). Apart from the original setting, they consider a stress-test scenario where the road is significantly more slippery than during NN training, namely \(50\%\) instead of \(20\%\). They finally decide to compare with optimal goal probabilities, computable via the probabilistic model checker mcsta, so that they can see whether any deficiencies are due to the NN, or are unavoidable given the high amount of noise.

The figure shows the outcome for Barto-large. One of the deficiencies is immediately apparent, the NN policy does not pass the stress test. Its goal probability matches the optimal values only near the goal line, and exhibits significant deficiencies elsewhere. Based on these insights, the quality analysts can now decide whether to relax the stress-test (after all, even optimal behavior here does not reach the goal with certainty), or whether to reject these NN polices and request re-training.

5.2 Learning Pipeline Analysis and Revision

More generally, DSMC can yield important insights not only for quality assurance, but also for the engineers designing the NN learning pipeline in the first place. There are two distinct scenarios:

  1. (i)

    The engineers run the same success tests as in quality assurance, and re-train if a test is not passed.

  2. (ii)

    The engineers assess different properties of interest to the learning process itself (e.g. expected length of policy runs), or assess the impact of different hyperparameter settings.

In both scenarios, the DSMC analysis results point to specific state-space regions that require improvement. This can be directly operationalized to revise the learning pipeline, by starting more training runs from states in the critical regions.

Figures 2 and 3 above have already demonstrated (i). Next we demonstrate (ii) through two case studies analyzing different hyperparameter settings.

Our first case study, in Fig. 4, analyzes the number n of training episodes, as a central hyperparameter of the learning pipeline. The only information available in deep Q-learning for the choice of this hyperparameter is the learning curve, i.e., the expected reward as a function of n, depicted on the right. Yet, as our DSMC analysis here shows, this information is insufficient to obtain reliable policies. In Barto-big, the highest reward is obtained after \(n=90000\) episodes. From \(n=70000\) to \(n=90000\), the reward slightly increases. Yet we see in Fig. 4 that the additional 20000 training episodes, while increasing overall goal probability, lead to highly deficient behavior in an area near the start of the map, where goal probability drops below 0.25. If provided with that information, the engineers can focus additional training on that area, for instance.

In our next case study, we assume that the NN engineers decide to analyze the impact of starting training runs on (a) the starting line vs. (b) random points anywhere on the map. Figure 5 shows the results for the Ring map, where they are most striking. In variant (a), the top part of the Racetrack was completely ignored by the learning process. Looking into this issue, one finds that, during training, the first solution happens to be found via the bottom route. From there on, the reinforcement learning process has a strong bias to that route, preventing any further exploration of other routes.

Phenomena like this are highly detrimental if the learnt policy needs to be broadly robust, across most of the environment. The deficiency is obvious given the DSMC analysis results, and these results make it obvious how the problem can be fixed. But neither can be seen in the learning curves.

Fig. 5.
figure 5

Goal probabilities in Ring for NN oracles where training was carried out with reinforcing runs from the start line only (left) vs. from anywhere on the map (right). (Color figure online)

Full size image

5.3 Computational Effort for the Analysis

As discussed, it can be highly demanding or infeasible to verify the input/output behavior of even a single NN decision episode, and that complexity is potentially compounded by the state space explosion problem when endeavoring to verify the behavior induced by an NN oracle. Deep statistical model checking carries promise as a “light-weight” approach to this formidable problem, as no state space needs to be stored and on the NN side it merely requires to call the NN on sample inputs. In addition, it is efficiently parallelizable, just like SMC. Yet (1) the approach might suffer from an excessive number of sample runs needed to obtain sufficient confidence, and/or (2) the overhead of NN calls might severely hamper its runtime feasibility.

Fig. 6.
figure 6

Heat maps showing computational effort needed by DSMC, measured by the number of sample runs performed by modes to analyze goal probability for each map location. Results shown for the policies induced by our learnt NN in the top row, vs. a simple hand-coded policy (see text) at the bottom. Each point on the map shows \(\lfloor \log _{2}(\# runs) \rfloor \). (Color figure online)

Full size image

Figure 6 shows data regarding (1). We compare the effort for analyzing our NN policies to that required for analyzing a conventional hand-made policy that we incorporated into our Jani models.Footnote 2 As the heat maps show, the latter effort is higher. This is due to a tendency to more risky behavior in the hand-made policy, resulting in higher variance. Regarding (2), the runtime overhead for NN calls is actually negligible in our study. Each call takes between 1 and 4 ms. There is an added overhead for constructing the NN once at the beginning of the analysis, but that takes at most 6 ms.

These results should of course not be over-interpreted, given the limitations of this initial study. But they do provide evidence that the computational overhead may be manageable in practice at least for moderate-size neural networks.

6 Conclusion

This paper has described the cornerstones of an effective methodology to apply statistical model checking as a light-weight approach to checking the behavior of systems incorporating neural networks. The most important aspects of the DSMC approach are its (i) genericity – in that it provides a generic and scalable basis for analyzing learnt action policies; its (ii) openness – since the approach is put into practice using the Jani format, supported by many tools for probabilistic or statistical model checking; and its (iii) focus – on an abstract fragment of the “autonomous driving” challenge. We consider these contributions as a conceptual nucleus of broader activities to foster the scientific understanding of neural network efficacy, by providing the formal and technological framework for precise, yet scalable problem analysis.

We have contributed an initial case study suggesting that this may indeed be useful and feasible. We hope that the study provides a compelling basis for further research on deep statistical model checking. Racetrack forms a viable starting point for this endeavor in that can be made more realistic in a manifold of dimensions: finer discretizations, different surface conditions, appearing/disappearing obstacles, other traffic participants, speed limits and other traffic regulations, different probabilistic perturbances, fuel efficiency, change from map perspective to ego-perspective of an autonomous vehicle, mediated by vision and other sensor systems. We are actually embarking on an exploration of these dimensions, focussing first on speed limits and random obstacles.

From a general perspective, DSMC provides a refined form of SMC for MDPs where thus far only implicitly defined random action policies have been available. If those were applied to Racetrack, goal probabilities \({<}0.1\) would result – except directly at the goal line. DSMC instead can harvest available data for a far better suited action policy, in the form of a NN oracle trained on the data at hand. Of course, other forms of oracles (based on, say, random forests) can be considered with DSMC rightaway, too.