iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/978-3-030-34152-7_14
A Fixed Charge Solid Transportation Problem with Possibility and Expected Value Approaches in Hybrid Uncertain Environment | SpringerLink
Skip to main content
Springer Nature Link
Log in

A Fixed Charge Solid Transportation Problem with Possibility and Expected Value Approaches in Hybrid Uncertain Environment

  • Conference paper
  • First Online:
Recent Advances in Intelligent Information Systems and Applied Mathematics (ICITAM 2019)

Part of the book series: Studies in Computational Intelligence ((SCI,volume 863))

Abstract

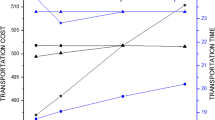
The main investigation of the paper is to develop the restricted fixed charge solid transportation problem under a hybrid uncertain environment where fuzziness and roughness coexist. A fuzzy rough STP model is developed by integrating the classical STP, fuzzy set theory, and rough set theory, which apparently provide a way to accommodate the uncertainty. For solving the problem, we apply the fuzzy rough expected value operator and propose the possibility based STP model with fuzzy rough parameters on a rough space. A numerical example is presented to describe the fuzzy rough approach using Lingo 13.0 optimization software. Finally, a graphical presentation has also shown to describe the comparison between two proposed approaches. Some important managerial decisions are also drawn by observing the optimal result.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 169.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 219.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 219.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Zadeh, L.A.: Concept of a linguistic variable and its application to approximate reasoning I. Inf. Sci. 8, 199–249 (1975)

    Article  MathSciNet  Google Scholar 

  2. Liu, S.T.: Fuzzy total transportation cost measures for fuzzy solid transportation problem. Appl. Math. Comput. 174, 927–941 (2006)

    MathSciNet  MATH  Google Scholar 

  3. Hitchcock, F.L.: The distribution of a product from several sources to numerous localities. J. Math. Phys. 20, 224–230 (1941)

    Article  MathSciNet  Google Scholar 

  4. Das, A., Bera, U.K., Das, B.: A solid transportation problem with mixed constraint in different environment. J. Appl. Anal. Comput. 6(1), 179–195 (2016)

    MathSciNet  Google Scholar 

  5. Haley, K.: The solid transportation problem. Oper. Res. 10, 448–463 (1962)

    Article  Google Scholar 

  6. Pawlak, Z., Skowron, A.: Rudiment of rough sets. Inf. Sci. 177, 3–27 (2007)

    Article  MathSciNet  Google Scholar 

  7. Kundu, P., Kar, S., Maiti, M.: Some solid transportation models with crisp and rough cost. Int. J. Math. Comput. Sci. Eng. 7(1), 13–20 (2013)

    Google Scholar 

  8. Shiraz, R.K., Charle, V., Jalalzadeh, L.: Fuzzy rough DEA model: a possibility and expected value approaches. Expert Syst. Appl. 41, 434–444 (2014)

    Article  Google Scholar 

  9. Pawlak, Z.: Rough sets. Int. J. Inf. Comput. Sci. 11(5), 341–356 (1982)

    Article  Google Scholar 

  10. Das, A., Bera, U.K., Maiti, M.: A profit maximizing solid transportation model under rough interval approach. IEEE Trans. Fuzzy Syst. 25(3), 485–498 (2016)

    Article  Google Scholar 

  11. Polkowski, L., Skowron, A. (eds.): Rough sets and current trends in computing. Lecture Notes in Artificial Intelligence, vol. 1424. Springer (1998)

    Google Scholar 

  12. Polkowski, L., Skowron, A. (eds.): Rough sets in knowledge discovery, vol. 1–2. Springer (1998)

    Google Scholar 

  13. Polkowski, L., Tsumoto, S., Lin, T.Y. (eds.): Rough set methods and applications–new developments in knowledge discovery in information systems. Springer (2000)

    Google Scholar 

  14. Zhong, N., Skowron, A., Ohsuga, S. (eds.): New direction in rough sets, data mining, and granular-soft computing, vol. 11. Springer (1999)

    Google Scholar 

  15. Das, A., Bera, U.K., Maiti, M.: A breakable multi-item multi stage solid transportation problem under budget with Gaussian type-2 fuzzy parameters. Appl. Intell. 45(3), 923–951 (2016)

    Article  Google Scholar 

  16. Das, A., Bera, U.K., Maiti, M.: Defuzzification of trapezoidal type-2 fuzzy variables and its application to solid transportation problem. J. Intell. Fuzzy Syst. 30(4), 2431–2445 (2016)

    Article  Google Scholar 

  17. Sinha, B., Das, A., Bera, U.K.: Profit maximization solid transportation problem with trapezoidal interval type-2 fuzzy numbers. Int. J. Appl. Comput. Math. 2(1), 41–56 (2016)

    Article  MathSciNet  Google Scholar 

  18. Zadeh, L.A.: Fuzzy Sets. Inf. Control 8, 338–353 (1965)

    Article  Google Scholar 

  19. Maity, G., Roy, S.K.: Solving a multi-objective transportation problem with nonlinear cost and multi-choice demand. Int. J. Manag. Sci. Eng. Manag. 11(1), 62–70 (2016)

    Google Scholar 

  20. Maity, G., Roy, S.K., Verdegay, J.L.: Multi-objective transportation problem with cost reliability under uncertain environment. Int. J. Comput. Intell. Syst. 9(5), 839–849 (2016)

    Article  Google Scholar 

  21. Roy, S.K., Maity, G., Weber, G.W.: Multi-objective two-stage grey transportation problem using utility function with goals. Cent. Eur. J. Oper. Res. 25(2), 417–439 (2017)

    Article  MathSciNet  Google Scholar 

  22. Roy, S.K., Maity, G., Weber, G.M., Gök, S.Z.: Conic scalarization approach to solve multi-choice multi-objective transportation problem with interval goal. Ann. Oper. Res. 253(1), 599–620 (2017)

    Article  MathSciNet  Google Scholar 

  23. Roy, S.K., Maity, G.: Minimizing cost and time through single objective function in multi-choice interval transportation problem. J. Intell. Fuzzy Syst. 32(3), 1697–1709 (2017)

    Article  Google Scholar 

  24. Maity, G., Roy, S.K.: Solving multi-objective transportation problem with interval goal using utility function approach. Int. J. Oper. Res. 27(4), 513–529 (2016)

    Article  MathSciNet  Google Scholar 

  25. Sun, Y., Zhang, G., Hong, Z., Dong, K.: How uncertain information on service capacity influences the intermodal routing decision: a fuzzy programming perspective. Information 9(1), 24 (2018)

    Article  Google Scholar 

  26. Zheng, Y., Liu, B.: Fuzzy vehicle routing model with credibility measure and its hybrid intelligent algorithm. Appl. Math. Comput. 176(2), 673–683 (2005)

    MathSciNet  MATH  Google Scholar 

  27. Mula, J., Peidro, D., Poler, R.: The effectiveness of a fuzzy mathematical programming approach for supply chain production planning with fuzzy demand. Int. J. Prod. Econ. 128(1), 136–143 (2010)

    Article  Google Scholar 

  28. Sun, Y., Hrušovský, M., Zhang, C., Lang, M.: A time-dependent fuzzy programming approach for the green multimodal routing problem with rail service capacity uncertainty and road traffic congestion. Complexity 2018(8645793), 22 (2018)

    MATH  Google Scholar 

  29. Kundu, P., Kar, S., Maiti, M.: Multi-objective multi-item solid transportation problem in fuzzy environment. Appl. Math. Model. 37(4), 2028–2038 (2013)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Management, National Institute of Technology Agartala, Jirania, West Tripura, 799046, India

    Dipanjana Sengupta & Anirban Dutta

  2. Department of Industrial Engineering, Pusan National University, Busan, South Korea

    Amrit Das

  3. Department of Mathematics, National Institute of Technology Agartala, Jirania, West Tripura, 799046, India

    Uttam Kumar Bera

Authors
  1. Dipanjana Sengupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amrit Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Anirban Dutta
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Uttam Kumar Bera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Uttam Kumar Bera .

Editor information

Editors and Affiliations

  1. Division of Graduate Studies and Research, Tijuana Institute of Technology, Tijuana, Mexico

    Oscar Castillo

  2. Haldia Institute of Technology, Haldia, West Bengal, India

    Dipak Kumar Jana

  3. Maulana Abul Kalam Azad University of Technology, Haringhata, India

    Debasis Giri

  4. Haldia Institute of Technology, Haldia, India

    Arif Ahmed

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Sengupta, D., Das, A., Dutta, A., Bera, U.K. (2020). A Fixed Charge Solid Transportation Problem with Possibility and Expected Value Approaches in Hybrid Uncertain Environment. In: Castillo, O., Jana, D., Giri, D., Ahmed, A. (eds) Recent Advances in Intelligent Information Systems and Applied Mathematics. ICITAM 2019. Studies in Computational Intelligence, vol 863. Springer, Cham. https://doi.org/10.1007/978-3-030-34152-7_14

Download citation

Publish with us

Policies and ethics

Search

Navigation