Keywords

1 Introduction

Road transport is still responsible for the bulk of transport emissions in terms of greenhouse gases and air pollutants. Every day, congested roads are a huge cost to the large cities in the world. However, profound change lies ahead for the transport sector in the world. A series of technological innovation and disruptive business models has led to a growing demand for new mobility services. At the same time, the sector is responding to the pressing need to make transport more efficient and sustainable. Digital technologies are a driving force of this process of innovation in transport sector. These technologies create a truly multimodal transport system integrating all modes of transport into one mobility service, allowing people and cargo to travel smoothly from door to door.

In this paper, we focus on the transportation service developed by Padam. The service consists in creating dynamic bus lines according to the customer demands. In Padam’s system, customers submit demands of transportation (origin and destination locations) via a mobile application, either in advance, i.e. few days before the service, or in real-time for an immediate service. Customers specify either when they wish to be picked up or when they have to be at their destination. The transportation service is operated by mini-bus with restricted number of places. All potential stop locations of buses are predefined and correspond to POI in cities where a bus can stop without affecting traffic, such as train or metro station, administrative buildings and so on. Thus, pickup and destination locations of customers are then associated to their nearest predefined locations and the customer will be serviced at these predefined locations instead of original pickup and destination locations. Once a customer submits its request, the Padam’s optimization service decides whether the request can be accepted or not, i.e. whether the request can be inserted in the existing rides or not. When solutions exist, several offers are then proposed to the customer around its requested time-window, among which he will choose the most convenient for himself. The transport operation is outsourced in Padam’s service, and contract is negotiated with third parties transport companies. In such contract, the number of mini-bus as well as the shifts of working hours of drivers is specified for each weekday. The number of mini-bus for each day is determined by Padam based on historical data of transportation demands. The starting locations of rides are decision variables fixed by the optimization engine depending on the number and the localization of requests of customers. Furthermore, as the transport cost is a fixed cost (i.e. outsourcing cost), the main objective of Padam’s service is servicing as many demands as possible during the ride shifts.

In this work, we improve optimization algorithm implemented in Padam’s service. More precisely, we consider a dynamic dial-a-ride problem with online requests of transportation. Since a solution must be proposed to a customer in real time, i.e. in a few seconds for each request, a heuristic approach is proposed. The proposed method is based on a neighborhood search algorithm for reinsertion of requests rejected by the online insertion algorithm. The Reinsertion Algorithm uses construction and destruction operators such as those used in an ALNS meta-heuristic [11]. It should be noted that the reinsertion techniques for the dynamic DARP are not widely used in the literature. To the best of our knowledge, only the paper [10] has proposed a reinsertion algorithm for dynamic DARP in which the objective is to reduce the number of vehicles while in our case the number of vehicles is imposed. The remainder of this paper is structured as follows. In Sect. 2 we provide a selective review on papers related to DARP problems. In Sect. 3 we give more details on the constraints and characteristics of our problem. In Sect. 4 we describe the proposed approach. Experimental results are presented in Sect. 5. The paper concludes with a short summary and an outlook on future research in Sect. 6.

2 Related Work

The Dial-a-Ride Problems (DARPs) have been investigated in the literature for over 30 years. The basic version of DARP consists of serving a set of users who specify their departure and arrival locations using a fleet of vehicles. The user specifies either desired pickup time or desired drop-off time. The basic objective function used in the literature is the total distance traveled by the vehicles [3]. There are two main versions of the problem: static and dynamic DARP. In the first case, all requests are known in advance before computing a solution while in the second case a part of the user requests arrives in real time, vehicle routes being adjusted in real-time to meet new demand. Dynamic DARP has received much less attention than its static counterpart. See [6] for a recent survey on both static and dynamic cases.

To solve dynamic DARP, literature studies have been focused on fast heuristics to insert new requests [7] and on meta-heuristic methods to optimize the system between the appearance of two consecutive requests [1, 12]. Most studies have proposed to combine the online insertion and the optimization system between requests [2, 4, 8, 14]. In [8], the authors proposed an online-regret based algorithm for a 2-phase optimization procedure by using available idle time to continuously optimize the solution. [2] presented hybrid method proceeding in two phases. In the first phase a simple insertion scheme is used to generate a feasible solution, which is improved in the second phase with a tabu search algorithm. The tabu search algorithm is stopped each time a new request appears. In [14], a similar approach to the one proposed by [2] has been developed to solve a real problem but the improvement phase uses an Adaptive Large Neighborhood Search metaheuristic. The study in [4] presented a two-phase insertion algorithm based on route perturbations. Every time a new request appears, the insertion is evaluated for each route within an appropriate neighborhood of the current one.

The aim of this paper is to design an efficient online reinsertion heuristic subject to a fixed and limited number of vehicles. By reinsertion heuristic we mean that whenever the online system cannot insert a new customer, we try to rearrange the current solution to try to insert him anyway. This procedure must be fast (the computation time must not exceed few seconds) To the best of our knowledge, only two papers have developed a reinsertion procedure for the DARP [9, 10]. In these two studies, the number of vehicles is unlimited, which is not the case in our problem. In [9], the authors developed a heuristic for the static multi-vehicles DARP in order to reduce the number of used vehicles. Their heuristic improves the parallel insertion heuristic of [7]. [10] adapts the latter algorithm to the dynamic case, where the main objective is to reduce the number of used vehicles.

In this paper, we present a new Reinsertion Algorithm for dynamic DARP based on destroy/repair operators. This algorithm allows us to test more reinsertion possibilities than the approach proposed in [9] and [10], while remaining fast and simple. We study the performance of our reinsertion heuristic both in terms of the vehicle duration and of the number of accepted requests. Extensive tests on real hard instances provided by Padam are performed.

3 Problem Description

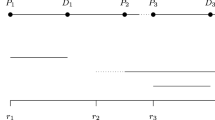
When a user wants to book a ride, he specifies (via a mobile application) temporal and geographical informations: pickup and drop-off locations, number of passengers and requested hour. The requested hour concerns either the desired pickup or drop-off time, in which case the customer’s request is said to be pickup-oriented (PO) or delivery-oriented (DO), respectively. This kind of choice is frequently used in Dial-A-Ride systems [3]. The road network is modeled as weighted graph with a set V of nodes and a set E of edges. Nodes represent predefined pickup and drop-off locations and each user’s request is associated to the nearest predefined location. Nodes are determined by a statistical study on user travel patterns by combining several data sources, which is not presented in this paper. The set of edges depicts paths between nodes, and each edge (i, j) has weights \(d_{ij}\) and \(t_{ij}\) which correspond to the shortest distance and the shortest travel time between nodes i and j, respectively.

A homogeneous fleet of vehicles fixed by the transporter is available to serve requests. Vehicles have their own time window (beginning and end of service) and start location. When the system receives a request, the optimization engine determines one or more proposals using a fast heuristic (described in Sect. 4.1), and the proposals are sent to the customer. When the customer confirms one of the proposals, the request is inserted in the appropriate ride and a time window constraint is added on the request (see Sect. 4.1). Furthermore, the system imposes a maximum ride time \(M_{ij}\) between pick-up i and drop-off j of each inserted request in a ride where \(M_{ij}\) is the maximum detour that a customer can accept and is proportional to the shortest travel time \(t_{ij}\) between i and j, i.e. \(M_{ij} \le \gamma _k\times t_{ij}\), with \(\gamma _k \ge 0\). The value of \(\gamma _k\) is selected from a set \(\varGamma \) of coefficients already predefined in the system and depends on the value of \(t_{ij}\). For example, for any travel time \(t_{ij}\) in the interval [10, 20] of minutes, the value of \(\gamma \) is 1.3. The set \(\varGamma \) helps us to models the fact that the acceptable deviation is not the same for short and long travel time. Thus, for each insertion of a new request, the optimization engine must respect time-window and gamma constraints of each already inserted request in addition to vehicle constraints, namely maximum capacity and service time window. The main goal is then to serve a maximum number of requests under described constraints while minimizing the service time duration of the vehicles. Given the dynamic nature of the problem, it is clear that it is not possible to directly maximize the number of served requests. Instead, our approach will use the total duration of the rides as an objective to be optimized, the duration of a ride being the sum of the travel time between it’s successive visited nodes. The idea is to create rides with fewer useless detour and with ‘straight’ travels so that they serve more requests at the end of the service.

4 Solving Approaches

In this section, we first present the algorithm currently used by the company. We call it the online insertion algorithm. We then present our new reinsertion heuristic algorithm designed to improve the responses of the system.

4.1 Online Insertion Algorithm

Each time a new request appears, a fast insertion heuristic is launched to get a quick proposal list for the customer (generally in less than 1 s time). This Online Insertion Algorithm is a greedy heuristic which tests each possible insertion position (i.e pickup/drop-off position) in each ride. If feasible insertions are found, the heuristic output several proposals that are submitted to the customer, each one at a different time like timetables in public transportation system. The idea is to take into account the wishes of the customer while keeping in the foreground the concept of shared transportation. The customer is free to choose one of the proposals or to refuse them. The proposals are differentiated by their pickup and drop-off hours. If h is the requested hour of the customer, we assume that the customer will accept a proposal if the pickup (drop-off) hour of a PO (DO) request is within \(TW_r = \left[ h - W, h + W\right] \), where the value of W is often around 20 min (see [14] for more details).

Let’s assume that the customer chooses a proposal with \(h_p\) and \(h_d\) as pickup and drop-off time. To ensure that subsequent insertions will not disturb the initial commitment toward the customer, we impose a time-window around the pickup (\(TW_p\)) and drop-off (\(TW_d\)) hours as follows:

$$\begin{aligned} TW_p = \left[ h_p - PWB, h_p + PWA\right] \end{aligned}$$
$$\begin{aligned} TW_d = \left[ h_d - DWB, h_d + DWA\right] \end{aligned}$$

where PWB, PWA, DWB, DWA are parameters fixed by the company. These time-windows (which can as tight as 10 min wide) ensure that subsequent clients can be inserted in the same ride while maintaining a high-quality service for the new customer.

4.2 Reinsertion Algorithm

When dealing with real situations, it can happen that a customer gets no satisfactory answer or even no answer at all. It means that the current arrangement of the rides doesn’t allow us to serve him. In this case, rather than simply letting the customer refuse proposals, we try to move other already inserted and not yet served requests to see whether we can find an arrangement allowing us to insert the new customer while respecting all the other constraints. The rearrangement must be done in a few seconds to keep a low response time to the customer. We call the corresponding heuristic the Reinsertion Algorithm. The algorithm is based on destroy/repair neighborhoods search [13]. The idea is to appropriately destroy part of the solution by removing existing requests and then reinserting them together with the new request. Thus, each iteration of the algorithm consists in a destroy/repair steps. Iterations are performed until the calculation time limit is reached and the best feasible solution found (if any) is chosen. The maximum operating time of the reinsertion heuristic is noted as MT. The purpose is to find a proposal close to the request hour of the customer (Sect. 4.1).

Algorithm 1 describes our reinsertion heuristic. It is different from a pure Large neighborhood Search (LNS) framework [13] in that once the search finds a new solution, it is no longer improved, but rather returns to the original solution. This is necessary for practical issues. Indeed, at this stage, we are not sure that the customer will validate our proposal. Even if he validates it, he can decide to do it a little time later, for example one minute later. It is possible that other requests may be accepted during this period, which could make the proposed insertion impossible. In order to design an effective validation procedure, we must keep the reinsertion process as simple as possible and disrupt the current solution as little as possible.

figure a

We now present the components of the Algorithm 1.

4.2.1 Destroy Step

Given the current arrangement of the rides, the first step of the algorithm is to choose a set of requests to be removed from their current places (destroy step). To achieve it, we use three different destroy operators. Each operator selects the requests to be removed among a list LI of already inserted requests in rides. Note that LI does not necessarily contain all requests. Indeed, it is not relevant to remove requests which are distant (in time) from the requested hour h of the new customer. We then define a time window \(\left[ h - W - T, h + W + T\right] \) with T a free parameter and restrict LI to requests whose pickup hour or drop-off hour is in the time window \(\left[ h - W - T, h + W + T\right] \). If T is too small, the set of candidate requests will be small and will not provide enough opportunity to insert the new customer. However, if it is too high, the search will spend a lot of time deleting requests that are not relevant to insert the new request. Section 5.2.1 studies the impact of several values of T. Beside the list of candidates for removal, destroy operators also receive the number k of requests to select. k is randomly chosen (at each iteration) between \(k_{min}\) and \(k_{max}\), which are two parameters. Furthermore, at each iteration, the destruction operator used is randomly selected. We now describe our three removal operators:

 

Random operator: :

Select k requests randomly.

Worst operator: :

Select the k requests with the largest savings, i.e. the difference between the objective value of the current solution and the objective value of solution once the requests are removed. In order to increase diversification, this operator is randomized as follow: all requests of LI are sorted in decreasing order of saving values in a list L. A random number y is sampled between 0 and 1 and the request at the position \(\lfloor y^{p_r}\vert L \vert \rfloor \) where \(\vert L\vert \) is the size of L and \(p_r\) a chosen parameter. This is repeated until k requests have been chosen.

Relatedness operator: :

Choose a request randomly and select \(k -1\) related requests. The relatedness measure between request i and j is defined as follow:

$$\begin{aligned} \frac{1}{2} \left( t_{p_i, p_j} + t_{d_i, d_j} \right) + \frac{1}{2} \left( |u_{p_i} - u_{p_j} |+ |u_{d_i} - u_{d_j} |\right) \end{aligned}$$

where \(p_i\) and \(d_i\) are respectively the pickup and drop-off nodes, \(u_{p_i}\) and \(u_{d_i}\) the service time of pickup and drop-off of request i and \(t_{n_1, n_2}\) the travel time between nodes \(n_1\) and \(n_2\). This operator is also randomized as for the worst operator. The parameter controlling the randomness is called \(p_w\). In this case \(p_w\) = \(p_r\).

 

4.2.2 Repair Step

Once the requests to be removed have been selected, they are removed from their current rides. We then try to reinsert them in the best way, including the request of the new customer. If all requests can be inserted while respecting constraints of the already existing requests, we obtain a feasible solution. To reinsert requests we use three repair operators. Each operator is always called during the repair process, in a sequential way. If several operators find a feasible solution, the best one is selected and used as the outcome of the current iteration (see Algorithm 2).

figure b

 

Deep Greedy operator: :

Perform the best insertion among all feasible insertions of all remaining requests to be reinserted. The best insertion is defined as the insertion with the minimal increase in the objective function.

Regret operator: :

Insert the request with the largest regret. The regret measure is defined in [5] and evaluates the difficulty to insert the request later. The idea is to find for each request i its best insertion in each vehicle k, with insertion cost \(c_{ik}\). We then construct a matrix in which each row represents a request and each column a vehicle. If no feasible insertion exists, an arbitrary large value is used instead. A regret of a request i is then computed as:

$$ \sum _{k} \left( c_{ik} - \min _{j} c_{ij}\right) $$

Request with largest regret is then chosen and inserted in its best position.

Priority Operator: :

The idea is to insert first requests at positions which will have small impact on others request insertion. To do this, we first select a request, then a ride to insert this request. The following steps are repeated until the number of requests to be inserted is reached: (1) for each request, compute (by testing all possible insertions) the number of rides in which it is possible to insert it, (2) take the request with the smallest number, (3) compute for each ride (where insertion of the selected request is possible) the number of requests that can be inserted into it, (4) take the ride with the smallest number.

 

5 Experiments

The purpose of this section is to assess the benefits of the Reinsertion Algorithm (Sect. 4.2) by running computer simulations on realistic data. The simulations were executed on a server with 16 Intel Processor Core cadenced to 3 GHZ. For each instance, we run a simulation with online algorithm as described in Sect. 4.1 to get reference results called RV. The Reinsertion Algorithm being stochastic, we run 10 simulations on each instance and use the average results called V for comparison for each experiment. When comparing V against a reference value RV, we compute the relative percentage improvement \(\frac{V - RV}{RV} * 100\).

5.1 Instances

We have 19 instances divided in two groups A and B. The groups A and B contain 10 and 9 instances respectively. Each group models a different real transport context, with different service and geographical features. Instances of the same group differ by the number of requests. Each instance is named \(G\_N\), where G is the group name and N the number of requests. Table 1 presents fleet information and geographical data of each Group. Column ‘Nodes’ indicates the number of nodes of the underlying graph (i.e all pickup/drop-off nodes), ‘Service Duration’ is the time span where vehicle serve customer, ‘Vehicle Capacity’ is the maximum capacity of a vehicle, ‘Area’ is the number of \(km^2\) covered by the set of nodes and ‘Fleet Size’ is the number of vehicles ‘Requests’ gives the minimum and maximum number of requests among the instances of the group. The two groups are very different: A is a large territory with short service span representing commuting transport (morning or evening) with mini-bus whereas B is far much smaller with larger bus running throughout the day, representing public transport in a neighborhood area.

Table 1. Characteristics of groups A and B
Full size table

Table 2 presents customer constraints of each Group. Columns PWA/PWB and DWA/DWB concern Time-Window range of requests as explained in Sect. 4.1, ‘Gamma Levels’ and ‘Gamma Values’ the gamma parameters (see Sect. 3), W is defined in Sect. 4.2 and DwellingTime represents the service time at each pickup or drop-off node, i.e the time requested for people to get in and out of the bus. All temporal parameters are expressed in minutes. Based on the knowledge of the various instances and the operational experience of the company, we can say that group A is harder than group B, mostly because the associated territory is more extended and the associated requests don’t follow easy geographical patterns.

Table 2. Service quality for each instance group
Full size table

5.2 Impact of Parameters

Before testing our Reinsertion Algorithm, we want to study the impact of its important parameters T and MT defined in Sect. 4.2. Concerning the values of free parameters, preliminary experiment led us to set \(k_{min}=3\), \(k_{max}=10\) and \(p_r=4\).

5.2.1 Impact of T

Our first objective is to evaluate the impact of the value of T (defined in Sect. 4.2) on the final percentage of served requests. In this evaluation, the maximum allowed time MT for the experiment is set to 1 s. The Fig. 2 shows the results of the experiments plotted separately for each group. The behavior on the two groups is pretty clear: the performance increases up to 15 min and then decreases when compared to \(T=15\). Thus, \(T=15\) has a better performance than \(T=0\) since it provides a large search space of solutions. The performance associated with values beyond 15 min decreases because more time is expended in removing non-relevant requests. The decrease in performance is different between the two groups. We observe that in group B, this performance deteriorates when T increases and falls below \(T=0\) for values greater than 60 min. However, we observe that in group A this performance tends to stabilize around an average value when \(T>15\) and always performs better than \(T=0\). Figure 1 gives us insights to explain this behavior. Neighborhood represents the average number of requests that are candidates for removal (size of the list LI see Sect. 4.2.1) and Feasible computes the proportion of the number of feasible moves in relation to all the moves tested by the algorithm. These values are obtained by running one simulation on each instance. We observe that the size of the neighborhoods is on average similar for both groups. However, it appears that finding feasible moves is more harder in group A, which confirms the hardness of these instances (cf. Sect. 5.1).

Fig. 1.
figure 1

Mean number of booking and feasible moves in Neighborhood according to the value of T for each Group

Full size image

We keep the value \(T=15\) for future experiments. The fact that the same value gives best results on both groups is probably related to the fact that the W values are similar (see Table 2).

Fig. 2.
figure 2

Relative improvement according to the value of T for each group of instances.

Full size image

5.2.2 Impact of Maximum Allowed Time

In this section, we are interested in varying the maximum time MT allowed for the Reinsertion Algorithm. We perform independent tests for each value of MT. Figure 3 shows the impact of the maximum allowed time on the two groups of instances. In group B, we observe significant improvement between 1 and 3 s. The gain continues to increase up to 5 s in a less significant way. The behavior is different in group A. We observe a clear improvement when passing from 1 to 2 s, but no clear improvement up to 5 s. We even observe that \(MT=3\) and \(MT=4\) perform slightly worse than \(MT=2\). These variations are mostly due to the stochastic nature of the algorithm and the natural variance it produces. The group B takes more advantage of the increase of maximum time than group A, probably for the same reasons as those given in Sect. 5.2.1.

Based on these observations, we choose to limit the maximum allowed time for the Reinsertion Algorithm to 3 s, considering that it allows to keep fast answer time and that it doesn’t degrade the performances. Note that 2 s could also be an acceptable value.

Fig. 3.
figure 3

Relative Improvement according to the maximum allowed time (seconds) for each group of instances.

Full size image

5.3 Benefits of Reinsertion

The purpose of this section is to evaluate the benefits of running the proposed Reinsertion Algorithm on dynamic Dial-a-Ride problems. We use the percentage of served requests as a metric to evaluate the performance of the Reinsertion Algorithm but we also show its impact on the total duration of rides (defined in Sect. 3), which is the objective minimized by algorithms implemented in Padam’s service.

Table 3 presents results for group A. It exposes results with 13 vehicles (number of vehicles used in practice for this group of instances) and also for 12 and 14 vehicles for each instance. The meaning of the columns is as follows: O is for the percentage of served requests with online algorithm (algorithm implemented in Padam’s service), O+R is the percentage of served requests with online and reinsertion algorithms, Imp is the relative improvement of reinsertion over online in terms of served requests and ImpD is the relative improvement of reinsertion over online in terms of total duration of the rides.

We first observe that instances of group A are very hard, because we are often far from satisfying all requests with the online algorithm. However, the Reinsertion Algorithm provides an improvement on almost all instances, with an average improvement of \(3.64\%\) (respectively \(4.56\%\) and \(5.95\%\)) with 13 vehicles (respectively with 12 and 14 vehicles). This is done with approximately the same rides duration, which shows that the reinsertion can satisfy more requests with similar vehicle costs. By comparing the results obtained with 12 and 13 vehicles, we observe that the online algorithm serves on average \(45.82 \%\) of requests with 12 vehicles compared to \(49.68 \%\) with 13 vehicles, while the reinsertion serves on average \(48.17\%\) with 12 vehicles. It means that despite the hardness of the instances, Reinsertion Algorithm fills more than half of the gap caused by the removal of a vehicle and even eliminates the need to add a vehicle in the case of the instance A_177 and A_120. The results also show that with 13 vehicles, the Reinsertion Algorithm succeeds in inserting on average as many requests as with the online algorithm with 14 vehicles, improving the result of some instances.

An analysis of the results obtained by varying the number of vehicles shows that the relative improvement of the online algorithm with 14 vehicles compared to the same algorithm with 13 vehicles is \(3.8\%\), and the relative improvement of the Reinsertion Algorithm is \(63\%\) when comparing 14 vehicles against 13 vehicles. Then, we can conclude that the relative improvement of the online algorithm is lower when passing from 13 to 14 vehicles, while the relative improvement of the Reinsertion Algorithm is significantly larger.

In rare cases, the Reinsertion Algorithm implies a deterioration in the percentage of served requests. We observe on most of theses instances that the final duration of the ride is nevertheless higher. This may be explained by the fact that the reinsertion process can sometimes accept hard requests that would otherwise have been rejected, degrading the rides too much and making it more difficult to insert some subsequent requests. This seems however to be quite rare.

Table 3. Performance of Reinsertion Algorithm on instances of group A.
Full size table
Table 4. Performance of Reinsertion Algorithm on instance of group B.
Full size table

Table 4 presents results for group B. These results are more consistent than for group A with an improvement in all instances. With 6 vehicles, the reinsertion gives an average improvement of \(7.07\%\) with approximately similar rides duration, which is a significant improvement. With 5 vehicles, the reinsertion achieves an average improvement of \(11.16 \%\) resulting on an average of \(81.48 \%\) of served requests. This average percentage is larger than the results achieved with the online algorithm with 6 vehicles. This is especially true on 6 instances (two-thirds of the group instances). It means that the Reinsertion Algorithm allows on average to save 1 vehicle out of 6, which corresponds to a considerable benefit for the transporter. This is also true when comparing results with 6 and 7 vehicles: reinsertion with 6 vehicles performs better than the online algorithm with 7 vehicles on all instances, meaning that the reinsertion prevents the transporter to add a vehicle while having better performances and similar costs. This is another huge benefit.

We also observe that with a fixed number of vehicles, the Reinsertion Algorithm tends to perform better when the number of requests increases. This could potentially be explained by the fact that the higher the number of requests, the more the online algorithm is far from optimal arrangement for these requests.

6 Conclusion

In this paper, we have studied a real problem of dynamic DARP raised by the company Padam. We have proposed an original and novel re-insertion algorithm for rejected requests based on repair and destroy operators. Our approach explores many reinsertion possibilities since it allows to cover a wide neighbourhood. We conducted extensive experiments on hard and realistic instances up to 1011 requests and 14 vehicles to evaluate the benefits of our proposed method. We have shown that it allows us to respond to a greater number of requests and that it saves an average of one bus on almost half of the cases, which is a significant advantage for Padam.