Abstract
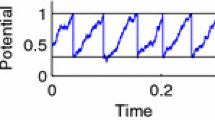
The Poisson process driven stochastic models of the neural activity and their diffusion approximation are studied. Two main studies are presented here: stochastic models driven by nonhomogeneous Poisson process with oscillatory intensity, and double compartment model with realistic synaptic inputs. The “phase lock” and the “amplitude lock” behaviour was observed in the model with oscillatory inputs and strong dependence on the initial phase after reset the membrane potential. Introducing the realistic synaptic input to the stochastic models opens new class of neuronal models: it has significant influence on all statistic parameters and the model behaviour. The double compartment model with realistic synaptic inputs is able to produce the bursting activity and this mechanism is described.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bernard C., Ge Y. C., Stockley E., Willis J. B., Wheal H. V.: Synaptic integration of NMDA and non-NMDA receptors in large neuronal network models solved by means of differential equations, Biol. Cyb. 70, 267–273 (1994)
Holden A. V.: Models of the Stochastic Activity of Neurons, Springer Verlag 1976
Kloeden E. P., Platen E.: Numerical Solution of Stochastic Differential Equations, Springer Verlag 1992
Lansky P., Rospars J. P., Valliant J.: Some Neuronal Models with Oscillatory Input, 1994
Lansky P., Smith C. E., Ricciardi L. M.: One-dimensional stochastic diffusion models of neuronal activity and related first passage time problems, Trends in Biological Cybernetics 1
Lewis P. A. W., Shedler G. S.:Simulation methods for Poisson processes in nonstationary systems, IBM research report 1978
Longtin A., Bulsara A., Pierson D., Moss F.: Bistability and the dynamics of periodically forced sensory neurons, Biol. Cyb. 70, 569–578, 1994
Musila M., Lansky P.: Simulation of a diffusion process with randomly distributed jumps in neuronal context. Int. J. Biomed Comput 31, 233–245, 1992
Musila M., Stochastic models of neuronal activity, Czech Technical University, PhD thesis 1990 (in Czech language)
Tuckwell H. C., Richter W.: Neuronal interspike time distributions and the estimation of neurophysiological and neuroanatomical parameters, J. Theor. Biol 71, 167–183, 1978
Tuckwell H. C.: Synaptic transmission in a model for stochastic neural activity J. Theor. Biol 77, 65–81, 1979.
Tuckwell, H. C.: Stochastic Processes in Neurosciences, Monash university 1989
Wilbur J. W., Rinzel J.: A theoretical basis for large coefficient of variation and bimodality in neuronal interspike interval distributions J. Theor. Biol 105, 345–368, 1983.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1995 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hruby, P. (1995). Stochastic neuronal models with realistic synaptic inputs and oscillatory inputs. In: Mira, J., Sandoval, F. (eds) From Natural to Artificial Neural Computation. IWANN 1995. Lecture Notes in Computer Science, vol 930. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-59497-3_186
Download citation
DOI: https://doi.org/10.1007/3-540-59497-3_186
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-59497-0
Online ISBN: 978-3-540-49288-7
eBook Packages: Springer Book Archive