Abstract
In this article we apply the analysis of eigensystems in Hilbert space for analyzing transaction data in real-time double auction markets. While this method is well known in quantum physics, its application for the analysis of financial markets is new. We show that transaction data from a properly designed financial accounting system of a market place completely reflect all market information and that this transaction data can be represented as Hermitian adjacency matrices without information loss.
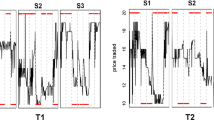
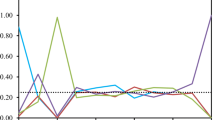
In this article we apply the analysis of the resulting eigensystem to detect and investigate market-making behavior. We show how some of the stylized facts about trading behavior can be recognized in the eigensystem of the market. We demonstrate the method in a small case study for a political stock market for the 2004 elections for the European Parliament in Germany.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
FORSYTHE, R., NELSON, F., NEUMANN, G. R., and WRIGHT, J. (1992): Anatomy of an experimental political stock market. The American Economic Review, 82(5), 1142–1161.
FRANKE, M., GEYER-SCHULZ, A., and HOSER, B. (2005): On the analysis of asymmetric directed communication structures in electronic election markets. In: T. Fent, A, Prskawetz, F. Billari, and J. Scheffran (Eds.): Proc. Agent-Based Computational Modelling in Demography 2003. Submitted.
GEYER-SCHULZ, A. (1991): An Introduction to Financial Accounting with APL2. Technical report, ACM SIGAPL, New York, N.Y.
HAKANSSON, N. H., BEJA, A., and KALE, J. (1985): On the feasibility of auomated market making by a programmed specialist. The Journal of Finance, 40(1), 1–20.
HOSER, B. and GEYER-SCHULZ, A. (2005): Eigenspectralanalysis of hermitian adjacency matrices for the analysis of group substructures. Journal of Mathematical Sociology. In press.
KATO, T. (1995): Perturbation Theory for Linear Operators. Springer, New York, 2 edition.
KLEINBERG, J. M. (1999).: Authoritative sources in a hyperlinked environment. JACM, 46(5), 604–632.
MEYER, C. D. (2000): Matrix Analysis and Applied Linear Algebra. Society for Industrial and Applied Mathematics, Philadelphia.
PAGE, L., BRIN, S., MOTWANI, R., and WINOGRAD, T. (1998): The Page Rank Citation Ranking: Bringing Order to the Web. Technical report, Computer Science Department, Stanford University.
SIMON, H. A. (2000): Administrative Behavior: A Study of Decision-Making Processes in Administrative Organizations. Free Press, New York, 4 edition.
SPANN, M. and SKIERA, B. (2003): Internet-based virtual stock markets for business forecasting. Management Science, 49(10), 1310–1326.
SPANN, M. and SKIERA, B. (2004). Einsatzmöglichkeiten virtueller Börsen in der Marktforschung. ZfB — Zeitschrift für Betriebswirtschaft (Ergänzungsheft), (2), 25–48.
STONE, M. H. (1932): Linear Transformations in Hilbert Space and their Applications to Analysis, volume 15 of American Mathematical Society, Colloquium Publications. American Mathematical Society, New York.
WASSERMANN, S. and FAUST, K. (1994): Social Network Analysis, Methods and Applications. Cambridge University Press, Cambridge.
WIENER BÖRSE AG (2002): Das Xetra Marktmodell. Technical report, Wiener Börse AG.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin · Heidelberg
About this chapter
Cite this chapter
Pranke, M., Geyer-Schulz, A., Hoser, B. (2005). Analyzing Trading Behavior in Transaction Data of Electronic Election Markets. In: Baier, D., Decker, R., Schmidt-Thieme, L. (eds) Data Analysis and Decision Support. Studies in Classification, Data Analysis, and Knowledge Organization. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-28397-8_25
Download citation
DOI: https://doi.org/10.1007/3-540-28397-8_25
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-26007-3
Online ISBN: 978-3-540-28397-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)