Abstract
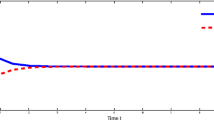
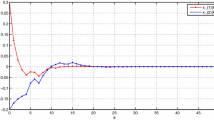
Many physical systems contains fast and slow phenomenons. In this paper we propose a dynamic neural networks with different time-scales to model the nonlinear system. Passivity-based approach is used to derive stability conditions for neural identifer. Several stability properties, such as passivity, asymptotic stability, input-to-state stability and bounded input bounded output stability, are guaranteed in certain senses. Numerical examples are also given to demonstrate the effectiveness of the theoretical results.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Amari, S.: Competitive and Cooperative Aspects in Dynamics of Neural Excitation and Self-organization. Competition Cooperation Neural Networks 20, 1–28 (1982)
Grossberg, S.: Adaptive Pattern Classification and Universal Recording. Biol. Cybern. 23, 121–134 (1976)
Ioannou, P.A., Sun, J.: Robust Adaptive Control. Prentice-Hall, Englewood Cliffs (1996)
Jagannathan, S., Lewis, F.L.: Identification of Nonlinear Dynamical Systems Using Multilayered Neural Networks. Automatica 32(12), 1707–1712 (1996)
Jin, L., Gupta, M.: Stable Dynamic Dackpropagation Learning in Recurrent Neural Networks. IEEE Trans. Neural Networks 10, 1321–1334 (1999)
Liu, H., Sun, F., Sun, Z.: Stability Analysis and Synthesis of Fuzzy Singularly Perturbed Systems. IEEE Transactions on Fuzzy Systems 13(2), 273–284 (2005)
Lu, H., He, Z.: Global Exponential Stability of Delayed Competitive Neural Networks with Different Time Scales. Neural Networks 18(3), 243–250 (2005)
Meyer-Baese, A., Pilyugin, S.S., Chen, Y.: Global Exponential Stability of Competitive Neural Networks With Different Time Scales. IEEE Trans. on Neural Networks 14(3), 716–719 (2003)
Ye, M., Zhang, Y.: Complete Convergence of Competitive Neural Networks with Different Time Scales. Neural Processing Letters 21(1), 53–60 (2005)
Yu, W., Poznyak, A.S.: Indirect Adaptive Control via Parallel Dynamic Neural Networks. IEE Proceedings - Control Theory and Applications 146(1), 25–30 (1999)
Yu, W., Li, X.: Some Stability Properties of Dynamic Neural Networks. IEEE Trans. Circuits and Systems, Part I 48(1), 256–259 (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Sandoval, A.C., Yu, W., Li, X. (2006). Passivity Analysis for Neuro Identifier with Different Time-Scales. In: Huang, DS., Li, K., Irwin, G.W. (eds) Intelligent Computing. ICIC 2006. Lecture Notes in Computer Science, vol 4113. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11816157_51
Download citation
DOI: https://doi.org/10.1007/11816157_51
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-37271-4
Online ISBN: 978-3-540-37273-8
eBook Packages: Computer ScienceComputer Science (R0)