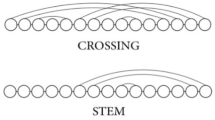
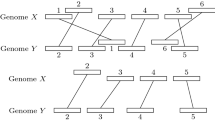
Abstract
Given two arc-annotated sequences (S,P) and (T,Q) representing RNA structures, the Arc-Preserving Subsequence (APS) problem asks whether (T,Q) can be obtained from (S, P) by deleting some of its bases (together with their incident arcs, if any). In previous studies [3, 6], this problem has been naturally divided into subproblems reflecting intrinsic complexity of arc structures. We show that APS(Crossing, Plain) is NP-Complete, thereby answering an open problem [6]. Furthermore, to get more insight into where actual border of APS hardness is, we refine APS classical subproblems in much the same way as in [11] and give a complete categorization among various restrictions of APS problem complexity.
This work was partially supported by the French-Italian PAI Galileo project number 08484VH and by the CNRS project ACI Masse de Données ”NavGraphe”.
Chapter PDF
Similar content being viewed by others
References
Alber, J., Gramm, J., Guo, J., Niedermeier, R.: Computing the similarity of two sequences with nested arc annotations. Theoretical Computer Science 312(2-3), 337–358 (2004)
Caetano-Anollés, G.: Tracing the evolution of RNA structure in ribosomes. Nucl. Acids. Res. 30, 2575–2587 (2002)
Evans, P.: Algorithms and Complexity for Annotated Sequence Analysis. PhD thesis, U. Victoria (1999)
Garey, M., Johnson, D.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman and Company, New York (1979)
Goldman, D., Istrail, S., Papadimitriou, C.H.: Algorithmic aspects of protein structure similarity. In: Proc. of the 40th Symposium of Foundations of Computer Science (FOCS 1999), pp. 512–522 (1999)
Gramm, J., Guo, J., Niedermeier, R.: Pattern matching for arc-annotated sequences. In: Agrawal, M., Seth, A.K. (eds.) FSTTCS 2002. LNCS, vol. 2556, pp. 182–193. Springer, Heidelberg (2002)
Guo, J.: Exact algorithms for the longest common subsequence problem for arc-annotated sequences. Master’s Thesis, Universitat Tubingen, Fed. Rep. of Germany (2002)
Jiang, T., Lin, G.-H., Ma, B., Zhang, K.: The longest common subsequence problem for arc-annotated sequences. In: Giancarlo, R., Sankoff, D. (eds.) CPM 2000. LNCS, vol. 1848, pp. 154–165. Springer, Heidelberg (2000)
Juan, V., Crain, C., Wilson, S.: Evidence for evolutionarily conserved secondary structure in the H19 tumor suppressor RNA. Nucl. Acids. Res. 28, 1221–1227 (2000)
Lancia, G., Carr, R., Walenz, B., Istrail, S.: 101 optimal PDB structure alignments: a branch-and-cut algorithm for the maximum contact map overlap problem. In: Proceedings of the 5th ACM International Conference on Computational Molecular Biology (RECOMB 2001), pp. 193–202 (2001)
Vialette, S.: On the computational complexity of 2-interval pattern matching. Theoretical Computer Science 312(2-3), 223–249 (2004)
Zhang, K., Wang, L., Ma, B.: Computing the similarity between RNA structures. In: Crochemore, M., Paterson, M. (eds.) CPM 1999. LNCS, vol. 1645, pp. 281–293. Springer, Heidelberg (1999)
Zuker, M.: RNA folding. Meth. Enzymology 180, 262–288 (1989)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Blin, G., Fertin, G., Rizzi, R., Vialette, S. (2005). What Makes the Arc-Preserving Subsequence Problem Hard?. In: Sunderam, V.S., van Albada, G.D., Sloot, P.M.A., Dongarra, J.J. (eds) Computational Science – ICCS 2005. ICCS 2005. Lecture Notes in Computer Science, vol 3515. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11428848_110
Download citation
DOI: https://doi.org/10.1007/11428848_110
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-26043-1
Online ISBN: 978-3-540-32114-9
eBook Packages: Computer ScienceComputer Science (R0)