Cayida llibre

Cayida llibre d'una pelota. Amuésense, por aciu fotografía estroboscópica, les posiciones de la pelota a intervalos regulares de tiempu: pa t = 1, 2, 3, 4, 5, ..., l'espaciu percorríu ye proporcional a 1, 4, 9, 16, 25, ..., etc.

En física, denominar cayida llibre al movimientu d'un cuerpu so l'acción esclusiva d'un campu gravitatoriu. Esta definición formal esclúi a toles cayíes reales influyíes en mayor o menor midida pola resistencia aerodinámica del aire, según a cualesquier otra que tenga llugar nel senu d'un fluyíu; sicasí, ye frecuente tamién referise coloquialmente a éstes como cayíes llibres, anque los efeutos de la mafa del mediu nun sían polo xeneral despreciables.

El conceutu ye aplicable tamién a oxetos en movimientu vertical ascendente sometíos a l'acción desaceleradora de la gravedá, como un disparu vertical; o a cualquier oxetu (satélites naturales o artificiales, planetes, etc.) n'órbita alredor d'un cuerpu celeste. Otros sucesos referíos tamién como cayida llibre constituyir les trayectories xeodésiques nel espaciu-tiempu descrites na teoría de la relatividá xeneral.

Exemplos de cayida llibre deportiva atopar n'actividaes basaes en dexase cayer una persona al traviés de l'atmósfera ensin sustentación alar nin de paracaíes mientres un ciertu trayeutu.

La cayida llibre como sistema de referencia

Un sistema de referencia amestáu a un cuerpu en cayida llibre puede considerase inercial o non inercial en función del marcu teóricu que se tea usando.

Na física clásica, la fuercia gravitatoriu que s'exerz sobre una masa ye proporcional a la intensidá del campu gravitatoriu na posición espacial onde s'atope dicha masa. La constante de proporcionalidad ye precisamente'l valor de la masa inercial del cuerpu, tal que establez el principiu d'equivalencia. Na física relativista, la gravedá ye l'efeutu que produz sobre les trayectories de los cuerpos la combadura del espaciu-tiempu; nesti casu, la gravedá nun ye una fuercia, sinón una xeodésica. Por tanto, dende'l puntu de vista de la física clásica, un sistema de referencia en cayida llibre ye un sistema aceleráu pola fuercia de la gravedá y, como tal, ye non inercial. Otra manera, dende'l puntu de vista de la física relativista, el mesmu sistema de referencia ye inercial, pos anque ta aceleráu nel espaciu, nun ta aceleráu nel espaciu-tiempu. La diferencia anicia na mesma definición de los conceutos xeométricu y cinemáticu, que pa cada marcu teóricu son dafechu distintos.

Cayida llibre ideal

Ver tamién: Ecuaciones pa un cuerpu en cayida llibre

Animación de la cayida llibre.

Na cayida llibre ideal, despréciase la resistencia aerodinámica que presenta l'aire al movimientu del cuerpu, analizando lo que pasaría nel vacíu. Neses condiciones, l'aceleración qu'adquiriría'l cuerpu sería debida puramente a la gravedá, siendo independiente de la so masa; por casu, si dexáramos cayer una bala de cañón y una pluma nel vacíu, dambos adquiriríen la mesma aceleración, $g\,$, que ye l'aceleración de la gravedá

Poro, partiendo d'un cuerpu (móvil) sometíu puramente a l'aceleración de la gravedá que ye constante en tol percorríu, tenemos.

$-g=constante$.

considerando vertical el exa y, col sentíu positivu escontra riba, l'aceleración de la gravedá ye vertical escontra baxo, polo que la señalamos con signu negativu:

${\cfrac {dv}{dt}}=-g$

$dv=-g\,dt$

$\int _{v_{0}}^{v_{1}}dv=-g\int _{t_{0}}^{t_{1}}dt$

$v_{1}-v_{0}=-g(t_{1}-t_{0})$

$v_{1}=v_{0}+-g(t_{1}-t_{0})$

la velocidá qu'algama'l móvil tiempu $t_{1}$ ye igual a la velocidá inicial $v_{0}$ que'l cuerpu tenía pa $t_{0}$ más l'aceleración de la gravedá $g\,$ pola medría de tiempu, si $t_{0}=0$ entós:

$v=v_{0}+-gt$

si'l cuerpu déxase cayer dende'l reposu $v_{0}=0$, entós:

$v=-gt$

pa determinar la posición, cuota y, tenemos que:

${\cfrac {dy}{dt}}=v=v_{0}+-gt$

$dy=(v_{0}+-gt)dt$

$\int _{y_{0}}^{y_{1}}dy=\int _{t_{0}}^{t_{1}}(v_{0}+-gt)dt$

$\int _{y_{0}}^{y_{1}}dy=v_{0}\int _{t_{0}}^{t_{1}}dt-g\int _{t_{0}}^{t_{1}}t\,dt$

$y_{1}-y_{0}=v_{0}(t_{1}-t_{0})-{\cfrac {1}{2}}g(t_{1}^{2}-t_{0}^{2})$

$y_{1}=y_{0}+v_{0}(t_{1}-t_{0})-{\cfrac {1}{2}}g(t_{1}^{2}-t_{0}^{2})$

si tomamos $t_{0}=0$:

$y=y_{0}+v_{0}\,t-{\cfrac {1}{2}}g\,t^{2}$

Nesta espresión tener en cuenta que se mide sobre'l exa y, tomando'l sentíu positivu en sentíu vertical escontra riba, tantu la posición como la velocidá y considérase como negativu'l sentíu vertical escontra baxo tocantes a la posición como tocantes a la velocidá o aceleración.

Ecuación del movimientu

D'alcuerdu a la segunda llei de Newton, la fuercia $\mathbf {F}$ qu'actúa sobre un cuerpu ye igual al productu de la so masa $m\,$ pola aceleración qu'adquier. En cayida llibre namái intervienen el pesu $\mathbf {P}$ (vertical, escontra baxo) y l'esfregadura aerodinámica $\mathbf {f} (v)$ na mesma direición, y sentíu opuestu a la velocidá. Dientro d'un campu gravitatoriu aproximao constante, la ecuación del movimientu de cayida llibre ye:

$\mathbf {F} =\mathbf {P} +\mathbf {f} =-mg{\mathbf {j} }-f{\frac {\mathbf {v} }{v}}=m{\frac {d\mathbf {v} }{dt}}$

L'aceleración de la gravedá $g\,$ lleva signu negativu porque se toma'l exa vertical como positivu escontra riba.

Trayeutoria en cayida llibre

Cayida llibre totalmente vertical

El movimientu del cuerpu en cayida llibre ye vertical con velocidá creciente (aproximao movimientu uniformemente aceleráu con aceleración g) (aproximao porque la velocidá aumenta cuando l'oxetu mengua n'altor, na mayoría de los casos la variación ye despreciable). La ecuación de movimientu puede escribise en términos l'altor y:

(1)$-mg+f=ma_{y}\,$

.

onde:

$a_{y},v_{y}\;$, son l'aceleración y la velocidá verticales.

$f\;$, ye la fuercia d'esfregadura fluidodinámico (qu'aumenta cola velocidá).

• Si, en primer aproximamientu, despréciase la fuercia d'esfregadura, cosa que puede faese pa cayíes dende pequeños altores de cuerpos relativamente compactos, nes que s'algamar velocidaes moderaes, la solución de la ecuación diferencial (1) pa les velocidaes y l'altor vienen dada por:

${\begin{matrix}v_{y}(t)=v_{0}-gt\\y(t)=h_{0}+v_{0}t-{\frac {1}{2}}gt^{2}\end{matrix}}$

onde v₀ ye la velocidá inicial, pa una cayida dende'l reposu v₀ = 0 y h₀ ye l'altor inicial de cayida.

• Pa grandes altores o oxetos de gran superficie (una pluma, un paracaíes) ye necesariu tener en cuenta la resistencia fluidodinámica que suel ser modelizada como una fuercia proporcional a la velocidá, siendo la constante de proporcionalidad la llamada esfregadura aerodinámica k_w:

(2)$-mg-k_{w}v_{y}=ma_{y}\,$

.

Nesti casu la variación col tiempu de la velocidá y l'espaciu percorríu vienen daos pola solución de la ecuación diferencial (2):

${\begin{cases}v_{y}=v_{0}y^{-k_{w}t/m}+{\cfrac {mg}{k_{w}}}(y^{-k_{w}t/m}-1)\\y=h_{0}-{\cfrac {mgt}{k_{w}}}-m\left({\cfrac {mg+k_{w}v_{0}}{k_{w}^{2}}}\right)(y^{-k_{w}t/m}-1)\end{cases}}$

Nótese que nesti casu esiste una velocidá llende dada pola esfregadura aerodinámicu y la masa del cuerpu que cai:

$v_{\infty }=\lim _{t\to \infty }v_{y}(t)=-{\frac {mg}{k_{w}}}$

• Un analís más cuidadosu del resfregón d'un fluyíu revelaría qu'a grandes velocidaes el fluxu alredor d'un oxetu nun puede considerase llaminar, sinón aturbolináu y prodúcense remolinos alredor del oxetu que cai de tal manera que la fuercia de resfregón vuélvese proporcional al cuadráu de la velocidá:

(3)$ma_{y}=m{\frac {d^{2}y}{dt^{2}}}=-mg-\epsilon {\frac {C_{d}}{2}}\rho A_{t}v_{y}^{2}$

Onde:

$C_{d}\;$, ye'l coeficiente aerodinámicu de resistencia a la meyora, que namái depende de la forma del cuerpu.

$A_{t}\;$, ye l'área tresversal a la direición del movimientu.

$\rho \;$, ye la densidá del fluyíu.

$\epsilon =\mathrm {sgn} (v_{y})\;$, ye'l signu de la velocidá.

La velocidá llende puede calculase fácilmente poniendo igual a cero l'aceleración na ecuación (3):

$v_{\infty }={\sqrt {\frac {2mg}{C_{d}\rho A_{t}}}}$

La solución analítica de la ecuación diferencial (3) depende del signu relativu de la fuercia d'esfregadura y el pesu polo que la solución analítica ye distinta pa un cuerpu que xube o pa unu que cai. La solución de velocidaes pa dambos casos ye:

${\begin{cases}v_{y}(t)={\sqrt {\cfrac {g}{\alpha }}}\tan \left(-t{\sqrt {{\alpha }{g}}}+\arctan \left(v_{0}{\sqrt {\cfrac {\alpha }{g}}}\right)\right)&\epsilon >0\\v_{y}(t)={\sqrt {\cfrac {g}{\alpha }}}\tanh \left(-t{\sqrt {{\alpha }{g}}}-{\mbox{arctanh}}\left(v_{0}{\sqrt {\cfrac {\alpha }{g}}}\right)\right)&\epsilon \leq 0\end{cases}}$

Onde: $\alpha =C_{d}\rho A_{t}/2m\;$.

Si intégrense les ecuaciones anteriores pal casu de cayida llibre dende un altor $h_{0}$ y velocidá inicial nula y pal casu de llanzamientu vertical dende un altor nulu con una velocidá inicial $v_{0}$ llógrense les siguientes resultaos pal altor del cuerpu:

Cayida llibre ($v_{y}(0)=0$ y $y(0)=h_{0}$):

$y(t)=h_{0}-{\cfrac {1}{\alpha }}\ln \left[\cosh \left(-t{\sqrt {{\alpha }{g}}}\right)\right]$

El tiempu trescurríu na cayida dende l'altor $y=h_{0}$ hasta l'altor $y=0$ puede llograse al reordenar la ecuación anterior:

$t(0)-t(h_{0})={\cfrac {1}{\sqrt {{\alpha }{g}}}}{\mbox{arccosh}}\left(y^{{\alpha }h_{0}}\right)$

Llanzamientu vertical ($v_{0}=v_{0}$ y $y(0)=0$):

$y(t)={\cfrac {1}{\alpha }}\ln \left[{\cfrac {\cos \left[-t{\sqrt {{\alpha }{g}}}+\arctan \left(v_{0}{\sqrt {\cfrac {\alpha }{g}}}\right)\right]}{\cos \left[{\mbox{arctan}}\left(v_{0}{\sqrt {\cfrac {\alpha }{g}}}\right)\right]}}\right]$

Si l'altor $h_{0}$ ye aquella en que la velocidá vertical faise cero, entós el tiempu trescurríu dende'l llanzamientu hasta l'intre en que s'algamar l'altor $h_{0}$ puede calculase como:

$t(h_{0})-t(0)={\cfrac {1}{\sqrt {{\alpha }g}}}{\mbox{arctan}}\left(v_{0}{\sqrt {\cfrac {\alpha }{g}}}\right)={\cfrac {1}{\sqrt {{\alpha }g}}}{\mbox{arccos}}\left(y^{-{\alpha }h_{0}}\right)$

Puede demostrase que'l tiempu que tarda un cuerpu en cayer dende un altor $h_{0}$ hasta'l suelu al traviés del aire ye mayor que'l que tarda'l mesmu cuerpu n'algamar l'altor máximu de $h_{0}$ si ye llanzáu dende'l suelu. Pa ello basta con probar la desigualdá siguiente:

${\mbox{arccosh}}\left(y^{{\alpha }h_{0}}\right)>{\mbox{arccos}}\left(y^{-{\alpha }h_{0}}\right)$

$\forall \alpha ,h_{0}>0$

sabiendo que ${\mbox{arccosh}}\left(y^{{\alpha }h_{0}}\right)\in \left[1,+\infty \right)$ y que ${\mbox{arccos}}\left(y^{-{\alpha }h_{0}}\right)\in \left[0,{\cfrac {\pi }{2}}\right]$

Intuitivamente la diferencia de tiempos ye clara, nel tiru escontra riba la velocidá inicial ye mayor polo que la fuercia d'esfregadura permediu a lo llargo de la trayeutoria tamién ye mayor que la que s'algamar en tiru escontra baxo.

Cayida llibre parabólica y cuasi-parabólica

Cuando un cuerpu cai en cayida llibre pero nun parte del reposu porque tien una velocidá non nula, entós la trayeutoria de cayida nun ye una recta sinón una curva aproximao parabólica. La ecuación de la trayeutoria en coordenaes cartesianes vien dada por:

(4)${\frac {dy}{dx}}={\frac {v_{y}}{v_{x}}}\qquad \qquad {\begin{cases}v_{y}(0)=0\\v_{x}(0)=V_{x}\end{cases}}\qquad \qquad {\begin{cases}y(0)=h_{0}\\x(0)=0\end{cases}}$

Esfregadura -k_wv. Trayectories cuasi parabóliques con esfregadura proporcional a la velocidá, pa cinco valores distintos de la velocidá horizontal β = 1,5 - 2,5 - 3,5 - 4,5, dende un altor h = 7δ.

Esfregadura -C_wv². Trayectories cuasi parabóliques con esfregadura proporcional al cuadráu de la velocidá, pa cinco valores distintos de la velocidá horizontal β = 1,5 - 2,5 - 3,5 - 4,5, dende un altor h = 7δ.

onde x ye la coordenada horizontal (exa de abcisas) y y la coordenada vertical (exa d'ordenaes).

La espresión de la velocidá vertical tien de reescribise en función de la coordenada x teniendo en cuenta que t = x/v_x. Pueden estremase los siguientes casos:

• Pa un cuerpu en cayida llibre ensin esfregadura, la trayeutoria ye esautamente una parábola dada por:

$y(x)=h_{0}-{\frac {gx^{2}}{2V_{x}^{2}}}$

• Cuando s'inclúi la esfregadura aerodinámica, la trayeutoria nun ye esautamente una parábola. Por casu pa una fuercia d'esfregadura proporcional a la velocidá como na (2) la trayeutoria resulta ser:

$y(x)=h_{0}-\delta \left[{\frac {x}{\beta \delta }}-\ln \left(1-{\frac {x}{\beta \delta }}\right)\right]$

onde:

$\delta =gm^{2}/k_{w}^{2}$

$\beta =V_{x}k_{w}/mg$

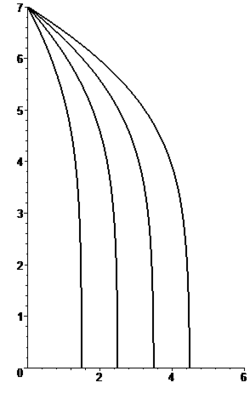
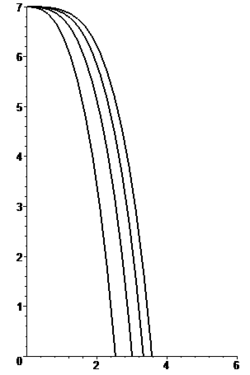
Pa una fuercia d'esfregadura proporcional al cuadráu de la velocidá, la integración de les ecuaciones del movimientu ye más complexa, presuponiendo fuercies d'esfregadura independientes en direición horizontal y vertical proporcionales al cuadráu del valor de la componente:

${\begin{cases}{\cfrac {dv_{x}}{dt}}=-C_{w}v_{x}^{2}\\{\cfrac {dv_{y}}{dt}}=+C_{w}v_{y}^{2}-g\end{cases}}$

La trayeutoria vien dada por:

$y(x)=h_{0}-\delta \ln \left[\cosh \left({\frac {y^{x/\delta }-1}{\beta }}\right)\right]$

onde:

$\delta =1/C_{w}$

$\beta ={\sqrt {g/(C_{w}V_{x}^{2})}}$

Les figures axuntes amuesen la forma de les trayectories pa cinco valores distintos del parámetru β pa una mesmu altor de cayida (midida n'unidaes de llargor δ).

Cayida llibre dende grandes altores

Artículu principal: Órbita

La cayida llibre dende grandes altores nun campu gravitatoriu aproximao esféricu, como ye'l casu del campu gravitatoriu terrestre, rique correiciones importantes yá que nesi casu nin la magnitú nin la direición de la fuercia gravitatoriu son constantes. Concretamente pa un campu gravitatoriu newtoniano con simetría esférica, cuando podemos ignorar la esfregadura cola atmósfera, la trayeutoria ye un arcu d'elipse.

Pal casu particular de cayida con velocidá inicial nula ensin esfregadura dende una distancia $r_{0}$ del centru del cuerpu de masa $M$, la trayeutoria ye una llinia recta y la espresión de la velocidá $v$ del cuerpu que cai, en función de la distancia $r$ al centru d'atraición gravitatoria xeneráu pola masa $M$ ye:

$v={\sqrt {2\ G\ M\ \left({\dfrac {1}{r}}-{\dfrac {1}{r_{0}}}\right)}}$

Mayor cayida llibre a la que se sobrevivió

El 26 de xineru de 1972, Vesna Vulović, azafata de les Aereollinies JAT, sobrevivió a una cayida llibre de 10.000 m cuando diba a bordu del vuelo 367. Una esplosión nel avión dio llugar a qu'ésti cayera sobre Srbská Kamenice, na entós Checoslovaquia (agora República Checa). La azafata sufrió frayatos nel craniu y en tres vértebres y tuvo en coma mientres 27 díes. Una vegada recuperada, comentó que, según l'home que lu atopó, ella atopábase na parte central del avión, con unu de los sos compañeros enriba. Una parte del so cuerpu taba dientro del fuselaxe, pero la cabeza taba per fora; un carrín de comíes claváu n'el so columna caltener dientro del avión. L'home que lu atopó, un médicu alemán que lu trató in situ, aseguró que tuvo muncha suerte. Años más tarde esta cayida foi desmentida, según aseguró'l corresponsal de la radiotelevisión pública alemana ARD en Praga, Peter Hornung-Andersen, "Lo más probable ye que l'avión foi baltáu pola fuercia aérea checoslovaca por cuenta de un error", afirma Hornung-Andersen, quien sorraya que "pa despintar l'incidente" los servicios secretos checoslovacos "inventáronse la hestoria de la cayida de la azafata" col impresionante récor d'altor.

Na segunda Guerra Mundial, hubo dellos informes sobre militares d'aviación que sobrevivieron a grandes cayíes. Nick Alkemade, Alan Magee, y Ivan Chisov cayeron a lo menos 5500 m.

La cayida llibre nun tien de confundir se con persones que sobreviven a vuelu controláu contra'l terrén.

Conozse que dos de les víctimes de Vuelu 103 de Pan Am sobrevivieron mientres un curtiu periodu de tiempu tres el choque del avión contra'l suelu (cola parte de lantre del avión fuselaxe na manera de cayida llibre), pero morrieron por cuenta de los sos graves mancaes primero que llegara l'ayuda.

Un paracaidista de Staffordshire llanzar dende un altor de 6,000 feet (1,800 m) ensin paracaíes en Rusia y vivió pa cuntalo. James Boole, de Tamworth, asegura qu'otru paracaidista tuvo de da-y una señal p'abrir el so paracaíes, pero la señal llegó-y dos segundos tarde. El señor Boole, que taba grabando al otru paracaidista pa un documental de televisión, aterrizó nuna zona de roques cubiertes por nieve, y sufrió frayatu de llombu y costiella.

Récores en cayida llibre

Según el llibru Guinness, el 14 d'ochobre de 2012 Felix Baumgartner batió tres récores históricos al llanzase en cayida llibre dende los 38.969,3 metros d'altor, dempués de xubir en globu tripuláu a la estratosfera, algamando una velocidá máxima de 1357,64 km/h.

Récor d'altor que depués rompió'l vicepresidente de Google, Alan Eustace, de 57 años, el 24 d'ochobre de 2014, saltando dende 41.425 metros, llogrando algamar una velocidá máxima de 1.322 km/h, rompiendo la barrera del soníu, anque nun superó la velocidá del récor de Baumgartner.

Mientres los últimos años de la década de los 50, el capitán estauxunidense Joseph Kittinger foi asignáu a los llaboratorios d'investigación médica aeroespacial, en Dayton, Ohio. Como parte del Proyeutu Excelsior d'investigación de la cayida llibre dende muncho altor, Kittinger fixo una serie de tres salto llevando traxes a presión.

El primer saltu, dende 23.290 m en payares de 1959 foi cuasi una traxedia porque hubo un error nel equipu. Anque'l paracaíes automáticu salvólu, aterrizó nun edificiu dando vueltes a 120 revoluciones per minutu, lo que causó la perda de conocencia de Kittinger. L'aceleración de les sos estremidaes llegó a superar 22 vegaes la de la gravedá, batiendo asina un nuevu récor. Tres selmanes dempués, volvió saltar dende 22.770 m. Por esi saltu foi premiáu cola medaya Leo Stevents de paracaidismu.

El 16 d'agostu de 1960, Kittinger realizó l'últimu saltu dende'l Excelsior III a 31.330 m utilizando un pequeñu parafrenos pa estabilizase. Cayó mientres 4 minutos y 36 segundos, algamando una velocidá máxima de 988 km/h antes d'abrir el so paracaíes a 4.270 m. La presión del so guante derechu falló mientres l'ascensu, y la so mano encher hasta algamar dos veces el tamañu normal. Kittinger batió los récores de xubida en globu más alta, saltu de paracaíes más altu, cayida más llarga (4 minutos) y velocidá más rápida alcanzada pol home na atmósfera.^{[ensin referencies]}

El domingu 14 d'ochobre de 2012, l'austriacu Felix Baumgartner del proyeutu Red Bull Stratos llogró saltar con paracaíes dende una cápsula sostenida na estratosfera por un globu d'heliu a aproximao 39.000 m d'altor, rompiendo tres récores mundiales, ente ellos los de cayida llibre dende mayor altitú y a mayor velocidá, superando mientres unos segundos la barrera del soníu.

Ver tamién

• Cayida llibre (deporte)
• Movimientu parabólicu
• Trayeutoria balística

Referencies

Bibliografía

• Marion, Jerry B. (1996). Dinámica clásica de les partícules y sistemes (en castellanu). Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
• Resnick, Robert & Krane, Kenneth S. (2001). Physics (n'inglés). Nueva York: John Wiley & Sons. ISBN 0-471-32057-9.
• Resnick, Robert & Halliday, David (2004). Física 4ª (en castellanu). CECSA, Méxicu. ISBN 970-24-0257-3.
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6ª (n'inglés), Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul A. (2000). Física pa la ciencia y la teunoloxía (2 volumes) (en castellanu). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.

Enllaces esternos

• Joe W. Kittinger y el pasu más altu del mundu artículu de Gregory Kennedy sobre'l proyeutu EXCELSIOR y el saltu de Kittinger en 1960

• Datos: Q140028
• Multimedia: Free fall