黑暗森林法則
黑暗森林法则是对人类未能发现外星文明的一种假想解释。该假说认为宇宙中存在许多外星文明,但它们都沉默而多疑。[1]该假说假设任何航天文明都会将其他智能生命视为不可避免的威胁,[2]并因此摧毁任何暴露其行蹤的新生文明。结果,电磁频谱会相对安静,没有任何智能外星生命的证据,就像在“黑暗的森林”中充满了“像幽灵一样在树林中潜行的武装猎人”。[3][4]天文学家和作家大卫布林在1983年对支持和反对费米悖论的论点的总结中描述了这个假说,[5]作为费米悖论的一个潜在解释。[6][7]黑暗森林假说这个概念后来被刘慈欣应用到他2008年发表的科幻小说《黑暗森林》中。[8][9]
背景
[编辑]目前,没有可靠或可重复的证据表明外星人曾访问过地球,[10][11]人类也未在除地球以外的任何地方发现或观察到智能外星生命的传输或证据。这与宇宙充满大量行星并且其中一些行星很可能宜居的知识背道而驰。生命通常会扩张、发展,直到它填满所有可用的生境。[12]这些相互矛盾的事实构成了费米悖论的基础,而黑暗森林假说是一种解释。
博弈论解读
[编辑]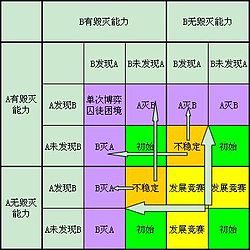
黑暗森林假说是博弈论中“顺序且不完全信息博弈”的一个特例。[13][7][14]
在博弈论中,“顺序且不完全信息博弈”是指所有参与者一个接一个依次轮流行动,但没有人知道所有可用信息的一种博弈。[15]在这个特定的博弈中,唯一的获胜条件是继续生存。[6]在“黑暗森林”这个特殊情形下,一个额外的限制是重要资源的稀缺性(有限性)。[7]“黑暗森林”可以被认为是一个扩展形式的博弈,每个玩家(文明)拥有以下可能的行动:摧毁玩家已知的另一个文明;广播和提醒其他文明某个玩家的存在;或者什么都不做。[13]
与费米悖论其它解说的关系
[编辑]黑暗森林假说与狂战士假说的不同之处在于,如果外星文明保持沉默,他们仍然存在。如果“致命的狂战士探测器”(由于资源稀缺)仅发送到显示出智能生命迹象的恒星系统,则我们可以将黑暗森林假说视为狂战士假说的一个特殊例子。[6]
参考
[编辑]- ^ Paradis, Justine. Outside/In[box]: What is the Dark Forest Theory?. New Hampshire Public Radio. 18 February 2022 [18 October 2022]. (原始内容存档于2022-12-29) (英语).
- ^ Vakoch, Douglas A. Hawking's fear of an alien invasion may explain the Fermi Paradox. Theology and Science. 3 April 2017, 15 (2): 134–138 [18 October 2022]. S2CID 219627161. doi:10.1080/14746700.2017.1299380. (原始内容存档于2022-10-21).
- ^ Liu, Cixin. The dark forest First. New York. 2015: 484. ISBN 9780765377081.
- ^ Hsu, Jeremy. China's 'Dark Forest' Answer to 'Star Wars' Optimism. Discover. October 31, 2015. (原始内容存档于October 17, 2022).
- ^ Brin, G. D. The Great Silence - the Controversy Concerning Extraterrestrial Intelligent Life. Quarterly Journal of the Royal Astronomical Society. 1 September 1983, 24: 283–309 [18 October 2022]. Bibcode:1983QJRAS..24..283B. ISSN 0035-8738. (原始内容存档于2022-10-19).
- ^ 6.0 6.1 6.2 Williams, Matt. Beyond "Fermi's Paradox" XVI: What is the "Dark Forest" Hypothesis?. Universe Today. 7 January 2021 [18 October 2022]. (原始内容存档于2022-10-18).
- ^ 7.0 7.1 7.2 Konior, Bogna. The Dark Forest: Theory of the Internet. BLOK Magazine. 6 July 2020 [18 October 2022]. ISSN 2719-4973. (原始内容存档于2022-12-08) (英语).
- ^ Kevra, Derek. Dark Forest theory: should we try to contact aliens?. FOX 2 Detroit. 11 October 2022 [18 October 2022]. (原始内容存档于2022-12-29).
- ^ Yu, C. The Dark Forest Rule: One Solution to the Fermi Paradox. Journal of the British Interplanetary Society. 1 January 2015, 68: 142–144 [18 October 2022]. Bibcode:2015JBIS...68..142Y. ISSN 0007-084X. (原始内容存档于2022-10-20).
- ^ Tingay, Steven. Is there evidence aliens have visited Earth? Here's what's come out of US congress hearings on 'unidentified aerial phenomena'. The Conversation. [27 October 2022]. (原始内容存档于2022-12-01) (英语).
- ^ Kolbert, Elizabeth. Have We Already Been Visited by Aliens?. The New Yorker. 14 January 2021 [27 October 2022]. (原始内容存档于2021-02-05).
- ^ Papagiannis, Michael D. "Are We All Alone, or could They be in the Asteroid Belt" by Michael D. Papagiannis, Quarterly Journal of the Royal Astronomical Society, Vol. 19, p.277. Quarterly Journal of the Royal Astronomical Society. 1978, 19: 277 [2022-10-27]. Bibcode:1978QJRAS..19..277P. (原始内容存档于2019-01-07).
- ^ 13.0 13.1 Yasser, Shehab. Aliens, The Fermi Paradox, And The Dark Forest Theory. Project Nash. 12 October 2020 [18 October 2022]. (原始内容存档于2022-10-20) (英语).
- ^ Fudenberg, Drew; Tirole, Jean. Sequential Bargaining with Incomplete Information. The Review of Economic Studies. April 1983, 50 (2): 221 [18 October 2022]. JSTOR 2297414. doi:10.2307/2297414. (原始内容存档于2022-10-20).
- ^ Ausubel, Lawrence M.; Cramton, Peter; Deneckere, Raymond J. https://www.sciencedirect.com/science/article/abs/pii/S1574000502030138
|chapterurl=缺少标题 (帮助). Aumann (编). Handbook of Game Theory with Economic Applications 3. 2002: 1897–1945 [2022-11-10]. ISBN 978-0-444-89428-1. doi:10.1016/S1574-0005(02)03013-8. (原始内容存档于2022-10-21).

