iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: http://www.ncbi.nlm.nih.gov/pubmed/24384152
Network diffusion accurately models the relationship between structural and functional brain connectivity networks - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Apr 15:90:335-47.
doi: 10.1016/j.neuroimage.2013.12.039. Epub 2013 Dec 30.

Network diffusion accurately models the relationship between structural and functional brain connectivity networks

Farras Abdelnour  1 , Henning U Voss  2 , Ashish Raj  2
Affiliations

Network diffusion accurately models the relationship between structural and functional brain connectivity networks

Farras Abdelnour et al. Neuroimage. .

Abstract

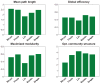
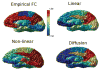
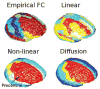
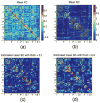
The relationship between anatomic connectivity of large-scale brain networks and their functional connectivity is of immense importance and an area of active research. Previous attempts have required complex simulations which model the dynamics of each cortical region, and explore the coupling between regions as derived by anatomic connections. While much insight is gained from these non-linear simulations, they can be computationally taxing tools for predicting functional from anatomic connectivities. Little attention has been paid to linear models. Here we show that a properly designed linear model appears to be superior to previous non-linear approaches in capturing the brain's long-range second order correlation structure that governs the relationship between anatomic and functional connectivities. We derive a linear network of brain dynamics based on graph diffusion, whereby the diffusing quantity undergoes a random walk on a graph. We test our model using subjects who underwent diffusion MRI and resting state fMRI. The network diffusion model applied to the structural networks largely predicts the correlation structures derived from their fMRI data, to a greater extent than other approaches. The utility of the proposed approach is that it can routinely be used to infer functional correlation from anatomic connectivity. And since it is linear, anatomic connectivity can also be inferred from functional data. The success of our model confirms the linearity of ensemble average signals in the brain, and implies that their long-range correlation structure may percolate within the brain via purely mechanistic processes enacted on its structural connectivity pathways.

Keywords: Brain connectivity; Functional connectivity; Networks; Structural connectivity.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Eight subjects’ Pearson correlation over two models. The left figure depicts the correlation for all subjects over values of c in the non-linear model, and the right figure shows the correlation behaviour of the proposed graph model as a function of diffusion time. Although the scale on x-axis has a different meaning in each case, the former being a mixing parameter whereas the latter is a diffusion time, both parameters serve a similar function. This is clearly seen in the similar behavior of each curve.
Figure 2
Figure 2
Scatter plots. Clockwise from top left: structure connectivity, linear functional model, network diffusion functional model, and non-linear functional model. Blue: frontal, cyan: parietal, green: occipital, orange: temporal, red: subcortical.
Figure 3
Figure 3
Eight subjects’ mean networks. Clockwise from top left: structural, empirical functional, empirical functional with intraconnected hemispheres, proposed network diffusion functional connectivities, non-linear (Honey et al.) model [36], and the linear model functional network.
Figure 4
Figure 4
Histograms resulting from randomizing structural and estimated functional networks. The resulting Pearson correlations for the randomized matrices are negligible while those obtained from the estimated network matrices are significant.
Figure 5
Figure 5
Pearson correlation resulting from sparsified structural connectivity matrix. Level of thresholding denoted as a fraction of maximum edge weight. The percentage of surviving edges varies from 39% (no thresholding) to about 1%. The proposed model maintains a high correlation up to about 10% of the edges surviving thresholding. Network metrics (Fig 6) are evaluated at 15% level
Figure 6
Figure 6
Various network measures of functional and structural networks evaluated at threshold level 15% (see Fig 5). Clockwise from top left: Mean path length, global efficiency, optimal community structure, and maximum modularity. The matrices are identified by ‘Struct’ (structural), ‘Fnctn’ (functional), ‘Lin’ (linear), and ‘Graph’ (graph diffusion)
Figure 7
Figure 7
Eight subjects’ mean color maps resulting from a seed placed at right posterior cingulum. Clockwise from top left: empirical functional, linear modeled functional, the proposed network diffusion functional connectivities, and non-linear (Honey et al. [36]) functional model.
Figure 8
Figure 8. Eight subjects’ mean color maps resulting from a seed placed at right frontal superior
Clockwise from top left: empirical functional, linear modeled functional, the proposed network diffusion functional connectivities, and non-linear (Honey et al. [36]) model.
Figure 9
Figure 9
Left: Estimate of the right superior motor area and right rectus connectivity from structure compared with fMRI-obtained connectivity over all eight subjects. The two regions are only functionally connected. The proposed model closely estimates the functional connectivity between the two nodes. Right: Estimate of the regions right frontal superior medial and right rectus connectivity from structure compared with fMRI-obtained connectivity over all eight subjects. The regions are both functionally as well as structurally connected.
Figure 10
Figure 10
Estimating structural connectivity from empirical functional connectivity (Fig 10(a)). Empirical structural connectivity is depicted in 10(b). Figures 10(c) and 10(d) show the estimated structural connectivity at SVD thresholds of 0.1 and 0.3, respectively. The connectivity matrices are arranged by lobes: ‘F’: frontal, ‘P’: parietal, ‘O’: occipital, ‘T’: temporal, ‘S’: subcortical. The nodes are arranged such that the left and right hemispheres nodes alternate in an odd-even fashion.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Achard S, Ed B. Efficiency and cost of economical brain functional networks. PLoS Comput Biol. 2007;3:e17. - PMC - PubMed
    1. Agaskar A, Lu YM. An uncertainty principle for functions defined on graphs. Vol. 8138. SPIE; 2011. p. 81380T.
    1. Albright TD. Direction and orientation selectivity of neurons in visual area MT of the macaque. Journal of Neurophysiology. 1984;52:1106–1130. - PubMed
    1. Alemán-Gómez Y, Melie-García L, Valdés-Hernandez P. BASPM: Toolbox for automatic parcellation of brain structures. Human Brain Mapping 2006
    1. Almond D, Budd C, McCullen N. Emergent behaviour in large electrical networks. In: Georgoulis EH, Iske A, Levesley J, editors. Approximation Algorithms for Complex Systems, Vol. 3 of Springer Proceedings in Mathematics. Springer; Berlin Heidelberg: 2011. pp. 3–26.

Publication types

LinkOut - more resources