A baseline for the multivariate comparison of resting-state networks
- PMID: 21442040
- PMCID: PMC3051178
- DOI: 10.3389/fnsys.2011.00002
A baseline for the multivariate comparison of resting-state networks
Abstract
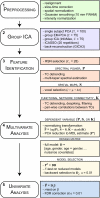
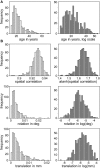
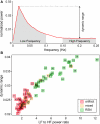
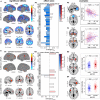
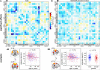
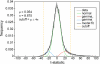
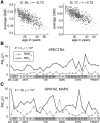
As the size of functional and structural MRI datasets expands, it becomes increasingly important to establish a baseline from which diagnostic relevance may be determined, a processing strategy that efficiently prepares data for analysis, and a statistical approach that identifies important effects in a manner that is both robust and reproducible. In this paper, we introduce a multivariate analytic approach that optimizes sensitivity and reduces unnecessary testing. We demonstrate the utility of this mega-analytic approach by identifying the effects of age and gender on the resting-state networks (RSNs) of 603 healthy adolescents and adults (mean age: 23.4 years, range: 12-71 years). Data were collected on the same scanner, preprocessed using an automated analysis pipeline based in SPM, and studied using group independent component analysis. RSNs were identified and evaluated in terms of three primary outcome measures: time course spectral power, spatial map intensity, and functional network connectivity. Results revealed robust effects of age on all three outcome measures, largely indicating decreases in network coherence and connectivity with increasing age. Gender effects were of smaller magnitude but suggested stronger intra-network connectivity in females and more inter-network connectivity in males, particularly with regard to sensorimotor networks. These findings, along with the analysis approach and statistical framework described here, provide a useful baseline for future investigations of brain networks in health and disease.
Keywords: connectome; fMRI; functional connectivity; independent component analysis; resting-state.
Figures

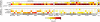

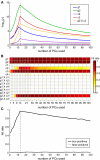
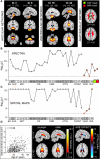
Similar articles
-
Long-term intensive gymnastic training induced changes in intra- and inter-network functional connectivity: an independent component analysis.Brain Struct Funct. 2018 Jan;223(1):131-144. doi: 10.1007/s00429-017-1479-y. Epub 2017 Jul 21. Brain Struct Funct. 2018. PMID: 28733834
-
Network-specific effects of age and in-scanner subject motion: a resting-state fMRI study of 238 healthy adults.Neuroimage. 2012 Nov 15;63(3):1364-73. doi: 10.1016/j.neuroimage.2012.08.004. Epub 2012 Aug 10. Neuroimage. 2012. PMID: 22992492
-
Identifying and characterizing resting state networks in temporally dynamic functional connectomes.Brain Topogr. 2014 Nov;27(6):747-65. doi: 10.1007/s10548-014-0357-7. Epub 2014 Jun 6. Brain Topogr. 2014. PMID: 24903106
-
Atypical Resting-State Functional Connectivity of Intra/Inter-Sensory Networks Is Related to Symptom Severity in Young Boys With Autism Spectrum Disorder.Front Physiol. 2021 Mar 24;12:626338. doi: 10.3389/fphys.2021.626338. eCollection 2021. Front Physiol. 2021. PMID: 33868000 Free PMC article.
-
Abnormal functional network connectivity among resting-state networks in children with frontal lobe epilepsy.AJNR Am J Neuroradiol. 2013 Dec;34(12):2386-92. doi: 10.3174/ajnr.A3608. Epub 2013 Jul 18. AJNR Am J Neuroradiol. 2013. PMID: 23868148 Free PMC article.
Cited by
-
Aberrant dynamic functional network connectivity in patients with diffuse axonal injury.Sci Rep. 2024 Nov 9;14(1):27386. doi: 10.1038/s41598-024-79052-4. Sci Rep. 2024. PMID: 39521859
-
White matter functional networks in the developing brain.Front Neurosci. 2024 Oct 23;18:1467446. doi: 10.3389/fnins.2024.1467446. eCollection 2024. Front Neurosci. 2024. PMID: 39507802 Free PMC article.
-
Sex Differences in Hierarchical and Modular Organization of Functional Brain Networks: Insights from Hierarchical Entropy and Modularity Analysis.Entropy (Basel). 2024 Oct 14;26(10):864. doi: 10.3390/e26100864. Entropy (Basel). 2024. PMID: 39451941 Free PMC article.
-
A Telescopic Independent Component Analysis on Functional Magnetic Resonance Imaging Data Set.bioRxiv [Preprint]. 2024 Sep 27:2024.02.19.581086. doi: 10.1101/2024.02.19.581086. bioRxiv. 2024. PMID: 39386484 Free PMC article. Preprint.
-
Frequency modulation increases the specificity of time-resolved connectivity: A resting-state fMRI study.Netw Neurosci. 2024 Oct 1;8(3):734-761. doi: 10.1162/netn_a_00372. eCollection 2024. Netw Neurosci. 2024. PMID: 39355435 Free PMC article.
References
-
- Allen E., Erhardt E., Eichele T., Mayer A. R., Calhoun V. D. (2010). “Comparison of pre-normalization methods on the accuracy of group ICA results”, in 16th Annual Meeting of the Organization for Human Brain Mapping, 6–10 June, Barcelona, Spain
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials


