iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: http://www.ncbi.nlm.nih.gov/pubmed/21052523
Correlated z-values and the accuracy of large-scale statistical estimates - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2010 Sep 1;105(491):1042-1055.
doi: 10.1198/jasa.2010.tm09129.

Correlated z-values and the accuracy of large-scale statistical estimates

Bradley Efron  1
Affiliations

Correlated z-values and the accuracy of large-scale statistical estimates

Bradley Efron. J Am Stat Assoc. .

Abstract

We consider large-scale studies in which there are hundreds or thousands of correlated cases to investigate, each represented by its own normal variate, typically a z-value. A familiar example is provided by a microarray experiment comparing healthy with sick subjects' expression levels for thousands of genes. This paper concerns the accuracy of summary statistics for the collection of normal variates, such as their empirical cdf or a false discovery rate statistic. It seems like we must estimate an N by N correlation matrix, N the number of cases, but our main result shows that this is not necessary: good accuracy approximations can be based on the root mean square correlation over all N · (N - 1)/2 pairs, a quantity often easily estimated. A second result shows that z-values closely follow normal distributions even under non-null conditions, supporting application of the main theorem. Practical application of the theory is illustrated for a large leukemia microarray study.

PubMed Disclaimer

Figures

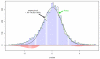
Figure 1
Figure 1
Histogram of z-values for N = 7128 genes, leukemia study, Golub et al. (1999). Dashed curve f̂(x), smooth fit to histogram; solid curve “empirical null”, normal density fit from central 50% of histogram, is much wider than theoretical 𝒩(0, 1) null distribution. Small red bars plotted negatively discussed in Section 4.
Figure 2
Figure 2
Comparison of exact formula for standard deviation of yk from (2.12) (heavy curve) with rms approxmation from (2.23) (dotted curve); N = 6000, α = .10 in (2.22), two classes as in (2.24). Dashed curve is standard deviation from (2.13) ignoring the correlation penalty. Hash marks indicate bin midpoints xk.
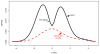
Figure 3
Figure 3
Comparison of exact formula for sd{F̂k} from Theorem 1 (heavy curve) with Rms approximation using (2.33) (dotted curve); same example as in Figure 2. Dashed curve shows standard deviation estimates ignoring the correlation penalty.
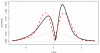
Figure 4
Figure 4
Leukemia data; two estimates of correlation penalty standard deviation sd1 {F̂k} for F̂k (2.27). Solid curve formula (3.12); dashed curve Rms approximation (2.33) using class estimates from Table 3. Dotted curve is independence estimate from (3.8), indicating that the correlation penalty is substantial.
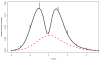
Figure 5
Figure 5
Simulation experiment for formula (1.4). Solid curve average of sd^, square root of (1.4), 100 replications, with bars indicating standard deviation of sd^ at x = −4, −3, …, 4; dotted curve exact sd from Figure 3; dashed curve average of sd^0, standard error estimate for F̂(x) ignoring correlation.
Figure 6
Figure 6
Solid curves show standard deviation of log(fdr^(x)) as a function of x at the upper percentiles of the z-value distribution for model (2.24), N = 6000 and α = 0, .1, .2. Dotted curves (green) same for log(Fdr^(x)) (4.5), nonparametric Fdr estimator. Dashed curves (red) for parametric version (4.17) of Fdr estimator.
Figure 7
Figure 7
Density of the z-value statistic (5.1) when t has a noncentral t distribution with ν = 20 degrees of freedom; for non-centrality parameter δ = 0, 1, 2, 3, 4, 5. The densities are seen to be nearly normal; dashed curves are exact normal densities matched in mean and standard deviation. For δ = 5, z has (mean,sd, skew,kurt) = (4.01, .71,−.06, .08). Negative values of δ give mirror image results. Remark G of Section 6 describes the density function calculations.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bolstad B, Irizarry R, Astrand M, Speed T. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–193. - PubMed
    1. Clarke S, Hall P. Robustness of multiple testing procedures against dependence. Ann. Statist. 2009;37:332–358.
    1. Csörgő S, Mielniczuk J. The empirical process of a short-range dependent stationary sequence under Gaussian subordination. Probab. Theory Related Fields. 1996;104:15–25.
    1. Desai K, Deller J, McCormick J. The distribution of number of false discoveries for highly correlated null hypotheses. Ann. Appl. Statist. 2009 Submitted, under review.
    1. Dudoit S, Laan M. J. van der, Pollard KS. Multiple testing. I. Single-step procedures for control of general type I error rates. Stat. Appl. Genet. Mol. Biol. 2004;3:71. Art. 13. electronic. - PubMed

Publication types

LinkOut - more resources