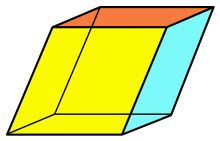
Romboedru

Descriere
Romboedru

Tip	prismă
Fețe	6 romburi
Laturi (muchii)	12
Vârfuri	8
χ	2
Configurația feței	V3.3.3.3
Grup de simetrie	C_i , [2⁺,2⁺], (×), ordin 2
Proprietăți	convex, zonoedru

În geometrie un romboedru^[1] este un poliedru cu șase fețe care sunt romburi. Este un caz particular al unui paralelipiped în care toate laturile (muchiile) au aceeași lungime. Poate fi folosit pentru a defini sistemul cristalin hexagonal, un fagure cu celule romboedrice. Un cub este un caz particular al unui romboedru, având toate fețele pătrate.

În general, un romboedru poate avea până la trei tipuri de fețe rombice în perechi opuse congruente, simetrie C_i de ordinul 2.

Patru puncte care formează vârfuri neadiacente ale unui romboedru sunt în mod necesar cele patru vârfuri ale unui tetraedru ortocentric și toate tetraedrele ortocentrice pot fi formate în acest fel.^[2]

Sistemul cristalin hexagonal

Articol principal: Sistem cristalin hexagonal.

Sistemul cristalin hexagonal are celule romboedrice, cu 6 fețe rombice congruente, formând un trapezoedru trigonal.

Cazuri particulare de simetrie

Formă	Cub	Trapezoedru trigonal	Prismă rombică dreaptă	Prismă rombică oblică
Condiții pt. unghiuri	$\alpha =\beta =\gamma =90^{\circ }$	$\alpha =\beta =\gamma$	$\alpha =\beta =90^{\circ }$	$\alpha =\beta$
Simetrie	O_h ordin 48	D_3d ordin 12	D_2h ordin 8	C_2h ordin 4
Fețe	6 pătrate	6 romburi congruente	2 romburi, 4 pătrate	6 romburi

Cub: cu simetrie O_h de ordinul 48. Toate fețele sunt pătrate.
Trapezoedru trigonal (numit și romboedru izoedric):^[3] cu simetrie D_3d de ordinul 12. Toate unghiurile interne neobtuze ale fețelor sunt egale (toate fețele sunt romburi congruente). Acest lucru poate fi observat la scalarea unui cub în direcția unei diagonale lungi a sa. De exemplu, un octaedru regulat cu două tetraedre regulate atașate pe fețe opuse formează un trapezoedru trigonal” cu unghiuri de 60°.
Prismă rombică dreaptă: cu simetrie D_2h de ordinul 8. Este format din două romburi și patru pătrate. Acest lucru poate fi observat la scalarea unui cub în direcția unei diagonale a unei fețe a sa. De exemplu, două prisme drepte cu baze triunghiulare regulate atașate împreună formează o prismă rombică dreaptă cu unghiuri de 60°.
Prismă rombică oblică: cu simetrie C_2h de ordinul 4. Are un singur plan de simetrie, prin patru vârfuri, și șase fețe rombice.

Geometrie în spațiu

La un romboedru izoedric cu lungimea laturii 1,^[3] cu unghiul ascuțit al romburilor $\theta ~$ , cu un vârf în origine (0, 0, 0) și cu o latură situată de-a lungul axei x, cei trei vectori generatori sunt

e₁ :

{\biggl (}1,0,0{\biggr )},

e₂ :

{\biggl (}\cos \theta ,\sin \theta ,0{\biggr )},

e₃ :

{\biggl (}\cos \theta ,{\cos \theta -\cos ^{2}\theta  \over \sin \theta },{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }{\biggr )}.

Alte coordonate se obțin prin adunarea vectorilor ^[4] din cele trei direcții: e₁ + e₂ , e₁ + e₃ , e₂ + e₃ și e₁ + e₂ + e₃ .

Volumul $V$ al unui romboedru izoedric cu latura de lungimea $a$ și unghiul ascuțit al romburilor $\theta ~$ se obține pe baza formulei pentru paralelipiped:

V=a^{3}(1-\cos \theta ){\sqrt {1+2\cos \theta }}=a^{3}{\sqrt {(1-\cos \theta )^{2}(1+2\cos \theta )}}=a^{3}{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }}~.

Altă relație:

V=2{\sqrt {3}}~a^{3}\sin ^{2}\left({\frac {\theta }{2}}\right){\sqrt {1-{\frac {4}{3}}\sin ^{2}\left({\frac {\theta }{2}}\right)}}~.

Deoarece aria bazei (rombice) este dată de $a^{2}\sin \theta ~$ , iar înălțimea unui romboedru este dată de volumul său împărțit la aria bazei sale, înălțimea $h$ a unui romboedru izoedric cu lungimea laturii $a$ și unghiul ascuțit al romburilor $\theta$ este dată de:

h=a~{(1-\cos \theta ){\sqrt {1+2\cos \theta }} \over \sin \theta }=a~{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }~.

Notă: $h=a~z$ ₃ , unde $z$ ₃ este a treia coordonată a e₃ .

Diagonala corpului dintre vârfurile unde se întâlnesc unghiurile ascuțite ale fețelor este cea mai lungă. Prin simetrie de rotație în jurul acelei diagonale, celelalte trei diagonale ale corpului, dintre cele trei perechi de vârfuri opuse în care apar și câte două unghiuri obtuze, au toate aceeași lungime.

Note

^ „romboedru” la DEX online
^ en Court, Nathan Altshiller (octombrie 1934), „Notes on the orthocentric tetrahedron”, American Mathematical Monthly, 41 (8): 499–502, doi:10.2307/2300415, JSTOR 2300415 .
^ ^a ^b en Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.
^ en „Vector Addition”. Wolfram. 17 mai 2016. Accesat în 17 mai 2016.

Legături externe

Portal Matematică

[1] „romboedru” la DEX online

[2] Court, Nathan Altshiller (octombrie 1934), „Notes on the orthocentric tetrahedron”, American Mathematical Monthly, 41 (8): 499–502, doi:10.2307/2300415, JSTOR 2300415 .

[:0-3] Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.

[4] „Vector Addition”. Wolfram. 17 mai 2016. Accesat în 17 mai 2016.

[1]

[2]

[3]

[4]