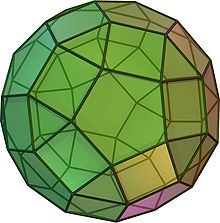
Rombicosidodecaedru

Rombicosidodecaedru
(animație și model 3D)
Descriere
Tip	Poliedru arhimedic (poliedru uniform)
Fețe	62 (20 triunghiuri, 30 pătrate, 12 pentagoane)
Laturi (muchii)	120
Vârfuri	60
χ	2
Configurația vârfului	3.4.5.4
Simbol Wythoff	3 5 | 2
Simbol Schläfli	rr{5,3} sau $r{\begin{Bmatrix}5\\3\end{Bmatrix}}$ t0,2{5,3}
Simbol Conway	eD sau aaD
Diagramă Coxeter
Grup de simetrie	Ih, H3, [5,3], (*532), ordin 120
Grup de rotație	I, [5,3]+, (532), ordin 60
Arie	≈ 59,306 a2   (a = latura)
Volum	≈ 41,615 a3   (a = latura)
Unghi diedru	3-4: 159° 05′ 41″ (159,09°) 4-5: 148° 16′ 57″ (148,28°)
Poliedru dual	Hexacontaedru romboidal
Proprietăți	Poliedru semiregulat, convex cu fețe poligoane regulate, tranzitiv pe vârfuri și laturi
Figura vârfului
Desfășurată

În geometrie rombicosidodecaedrul este un poliedru arhimedic. Are 62 de fețe regulate (20 triunghiulare și 30 pătrate și 12 pentagonale), 120 de laturi (muchii) identice și 60 de vârfuri identice, ca urmare este tranzitiv pe vârfuri și pe laturi. Are simetrie icosaedrică, ca și icosaedrul și dodecaedrul.

Dualul său este hexacontaedrul romboidal.

Are indicele de poliedru uniform U₂₇, indicele Coxeter C₃₀ și indicele Wenninger W₁₄.

Nume

Johannes Kepler în Harmonices Mundi (1618) a numit acest poliedru rombicosidodecaedru, fiind prescurtarea de la romb icosidodecaedric trunchiat, unde romb icosidodecaedric era numele dat de el triacontaedrului rombic. Există diferite trunchieri ale unui triacontaedru rombic într-un rombicosidodecaedru topologic: în mod evident rectificarea (la stânga între cele trei imagini de mai sus), cea care creează un poliedru uniform (în centru) și rectificarea dualului icosidodecaedrului (la dreapta), care este nucleul compusului dual.

Poate fi numit și un dodecaedru sau icosaedru expandat sau cantelat, din operațiunile de trunchiere pe oricare poliedru uniform.

Dual: Hexacontaedru romboidal

Coordonate carteziene

Coordonatele carteziene ale vârfurilor unui rombicosidodecaedru centrat în origine, cu lungimea laturii de 2, sunt toate permutările pare ale:

$\left(\,\pm 1,\,\pm 1,\,\pm \varphi ^{3}\,\right)$

$\left(\,\pm \varphi ^{2},\,\pm \varphi ,\,\pm \,2\varphi \,\right)$

$\left(\,\pm (2+\varphi ),\,0,\,\pm \varphi ^{2}\,\right)$

unde $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ este secțiunea de aur. Prin urmare, raza sferei circumscrise acestui rombicosidodecaedru (sfera care trece prin toate vârfurile sale) este distanța comună a acestor puncte față de origine, și anume ${\sqrt {\varphi ^{6}+2}}={\sqrt {8\varphi +7}}$ pentru lungimea laturii egală cu 2. Pentru lungimea laturii 1, această valoare trebuie înjumătățită, adică

$R={\frac {\sqrt {8\varphi +7}}{2}}={\frac {\sqrt {11+4{\sqrt {5}}}}{2}}\approx 2,233.$

Arie și volum

Aria A și volumul V ale unui rombicosidodecaedru cu lungimea laturii a sunt:

${\begin{aligned}A&=\left(30+5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}&&\approx 59,305\,982\,844\,9~a^{2}\\V&={\frac {60+29{\sqrt {5}}}{3}}a^{3}&&\approx 41,615\,323\,782\,5~a^{3}\end{aligned}}$

Relații geometrice

Dacă se expandează un icosaedru depărtând fețele lor de origine la o distanță potrivită, fără a modifica orientarea sau dimensiunea fețelor și se face același lucru cu dual său, dodecaedrul, iar apoi se „peticesc” găurile pătrate rezultate, se obține un rombicosidodecaedru. Prin urmare, are același număr de triunghiuri ca un icosaedru și același număr de pentagoane ca un dodecaedru, cu câte un pătrat pentru fiecare latură a fiecăruia.

Alternativ, dacă se expandează cinci cuburi depărtând fețele lor de origine la o distanță potrivită și se rotesc astfel încât să fie la 72° și echidistante, iar apoi se peticesc găurile pentagonale și triunghiulare rezultate, se obține un rombicosidodecaedru. Prin urmare, are același număr de pătrate ca și cinci cuburi.

Rombicosidodecaedrul are același aranjament al vârfurilor cu micul dodecaedru trunchiat stelat și cu compușii uniformi de șase sau douăsprezece prisme pentagramice.

Douăsprezece dintre cele 92 de poliedre Johnson sunt derivate din rombicosidodecaedru, patru dintre ele prin rotirea uneia sau mai multor cupole pentagonale: girat (J72), parabigirat (J73), metabigirat (J74) și trigirat (J75). Alte opt pot fi construite prin îndepărtarea a până la trei cupole, uneori rotind una sau mai multe dintre celelalte cupole (J76–J83) (v. mai jos).

Proiecții ortogonale

Rombicosidodecaedrul are șase proiecții ortogonale particulare, centrate pe un vârf, pe două tipuri de laturi și pe trei tipuri de fețe: triunghi, pătrat și pentagon. Ultimele două corespund cu planele Coxeter A₂ și H₂.

Proiecții ortogonale

Centrată pe	Vârf	Latura 3-4	Latura 5-4	Fața pătrat	Fața triunghi	Fața pentagon
Imagine
Cadru de sârmă
Simetrie proiectivă	[2]	[2]	[2]	[2]	[6]	[10]
Imagine dual

Pavare sferică

Rombicosidodecaedrul poate fi reprezentat și ca o pavare sferică și proiectat în plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu ariile sau lungimile. Liniile drepte pe sferă sunt proiectate în plan ca arce de cerc.

	centrată pe pentagon	centrată pe triunghi	centrată pe pătrat
Proiecție ortogonală	Proiecții stereografice

Poliedre înrudite

Expandarea fie a unui dodecaedru, fie a unui icosaedru creează un rombicosidodecaedru

Familia de poliedre icosaedrice uniforme
Simetrie: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duale ale poliedrelor uniforme
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Variante de simetrie

Acest poliedru este înrudit din punct de vedere topologic ca parte a secvenței de poliedre cantelate cu figurile vârfului (3.4.n.4) și continuă ca pavări ale planului hiperbolic. Aceste figuri tranzitive pe vârfuri au simetrie de reflexie *n32 în notația orbifold.

Variante de pavări expandate cu simetrie *n32: 3.4.n.4
Simetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paracomp.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Imagine
Vârf	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

Poliedre Johnson

Există 12 poliedre Johnson înrudite, 5 prin diminuare și 8 care conțin și rotații (girări):

Diminuate

J5

J76

J80

J81

J83

Girate și/sau diminuate

J72	J73	J74	J75
J77	J78	J79	J82

Aranjamentul vârfurilor

Rombicosidodecaedrul are în comun aranjamentul vârfurilor cu trei poliedre uniforme neconvexe: micul dodecaedru trunchiat stelat, micul dodecicosidodecaedru (având în comun fețele triunghiulare și pentagonale) și micul rombidodecaedru (având în comun fețele pătrate).

De asemenea, are în comun aranjamentul vârfurilor cu compușii poliedrici de șase sau douăsprezece prisme pentagramice.

Rombicosidodecaedru	Micul dodecicosidodecaedru	Micul rombidodecaedru
Micul dodecaedru trunchiat stelat	Compus de șase prisme pentagramice	Compus de douăsprezece prisme pentagramice

Bibliografie

• en Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3-9)
• en Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2. 

Vezi și

• Lista poliedrelor uniforme

Legături externe

• Materiale media legate de rombicosidodecaedru la Wikimedia Commons
• en Eric W. Weisstein, Small Rhombicosidodecahedron la MathWorld.
• en Eric W. Weisstein, Rombicosidodecaedru la MathWorld.
• en Editable printable net of a Rhombicosidodecahedron with interactive 3D view
• en The Uniform Polyhedra
• en Virtual Reality Polyhedra The Encyclopedia of Polyhedra

• en Klitzing, Richard. „3D uniform polyhedra”.  Cheie: srid