iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: http://pubmed.ncbi.nlm.nih.gov/39554240/
Opportunities and challenges of diffusion models for generative AI - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2024 Oct 3;11(12):nwae348.
doi: 10.1093/nsr/nwae348. eCollection 2024 Dec.

Opportunities and challenges of diffusion models for generative AI

Minshuo Chen  1 , Song Mei  2 , Jianqing Fan  3 , Mengdi Wang  1
Affiliations
Review

Opportunities and challenges of diffusion models for generative AI

Minshuo Chen et al. Natl Sci Rev. .

Abstract

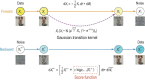
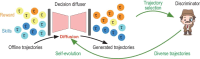
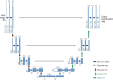
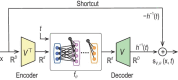
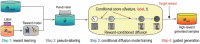
Diffusion models, a powerful and universal generative artificial intelligence technology, have achieved tremendous success and opened up new possibilities in diverse applications. In these applications, diffusion models provide flexible high-dimensional data modeling, and act as a sampler for generating new samples under active control towards task-desired properties. Despite the significant empirical success, theoretical underpinnings of diffusion models are very limited, potentially slowing down principled methodological innovations for further harnessing and improving diffusion models. In this paper, we review emerging applications of diffusion models to highlight their sample generation capabilities under various control goals. At the same time, we dive into the unique working flow of diffusion models through the lens of stochastic processes. We identify theoretical challenges in analyzing diffusion models, owing to their complicated training procedure and interaction with the underlying data distribution. To address these challenges, we overview several promising advances, demonstrating diffusion models as an efficient distribution learner and a sampler. Furthermore, we introduce a new avenue in high-dimensional structured optimization through diffusion models, where searching for solutions is reformulated as a conditional sampling problem and solved by diffusion models. Lastly, we discuss future directions about diffusion models. The purpose of this paper is to provide a well-rounded exposure for stimulating forward-looking theories and methods of diffusion models.

Keywords: diffusion model; generative AI; optimization; sample generation under controls.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Demonstration of forward and backward processes in diffusion models. The forward process is a noise corruption process, where Gaussian noise of increasing variance is progressively added to the clean data. The backward process is used for new sample generation starting from a standard Gaussian distribution, where the score function steers the generation process.
Figure 2.
Figure 2.
Conditional diffusion models generate images under various guidance. The upper row demonstrates an alignment with text description consisting of multiple objects. The lower row demonstrates an abstract description of aesthetic quality. Reproduced with permission from Black et al. [32].
Figure 3.
Figure 3.
Decision Diffuser and AdaptDiffuser in [59] and [61], respectively. Decision diffuser is trained on offline-labeled trajectories and is capable of generating new trajectories conditioned on desired reward values, or skills. AdaptDiffuser introduces a self-evolution loop utilizing selected high-quality trajectories from a trainable discriminator.
Figure 4.
Figure 4.
U-Net architecture for formula image resolution RGB images. When generating new samples using a discretized backward process, diffusion models utilize U-Net at each discretization step for transforming samples. The image sample together with a time embedding is first compressed into a low-dimensional representation and then lifted back to the original dimension. Reproduced with permission from Ronneberger et al. [70]. Copyright 2015 Springer.
Figure 5.
Figure 5.
Simplified U-Net architecture for approximating score functions in the low-dimensional subspace data setting. Matrix V represents the linear encoder and decoder, which is to be jointly learned with parameter formula image during the optimization of loss (12). Here formula image is a network with input and output dimensions being the subspace dimension. formula image is the score network parameterized by V and formula image. Reproduced with permission from Chen et al. [40].
Figure 6.
Figure 6.
The effect of guidance strength formula image on a three-component GMM in formula image [47,107]. Each component has weight formula image and identity covariance, and the component centers are formula image, formula image and formula image. The leftmost panel displays the unguided density. We increase the guidance strength from left to right. When generating samples, we use the ground truth score. Reproduced with permission from Wu et al. [107].
Figure 7.
Figure 7.
Illustration of a negative effect of large guidance strength. In this plot, the component means of the Gaussian mixture model are aligned on the same line. We increase the guidance strength formula image from left to right. The upper row uses a relatively large discretization step size in the backward process. With a large formula image, the center component splits into two clusters at an earlier stage. The bottom row uses a much smaller discretization step size; the center component then splits only with a much larger formula image. Reproduced with permission from Wu et al. [107].
Figure 8.
Figure 8.
Reformulation of data-driven black-box optimization as conditional sampling in [67]. The conditional distribution takes the targeted function value as the conditioning and is learned from a pre-collected data set. Reproduced with permission from Li et al. [67].
Figure 9.
Figure 9.
The learning algorithm proposed in [67] consists of four steps. In the first step a reward model is learned from the labeled data formula image. In the second step, the learned reward model is deployed as a pseudo-labeler to label formula image. In the third step, a conditional diffusion model is trained using the pseudo-labeled data. Lastly, in the fourth step, new samples are generated from the conditional distribution formula image by specifying a target reward value a. Reproduced with permission from Li et al. [67].
See this image and copyright information in PMC

References

    1. Bommasani R, Hudson DA, Adeli E et al. On the opportunities and risks of foundation models. arXiv: 2108.07258.
    1. Giuffrè M, Shung DL. Harnessing the power of synthetic data in healthcare: innovation, application, and privacy. NPJ Digit Med 2023; 6: 186.10.1038/s41746-023-00927-3 - DOI - PMC - PubMed
    1. Yang L, Zhang Z, Song Y et al. Diffusion models: a comprehensive survey of methods and applications. ACM Comput Surv 2024; 56: 105.10.1145/3626235 - DOI
    1. Stokel-Walker C, Van Noorden R. What ChatGPT and generative AI mean for science. Nature 2023; 614: 214–6. - PubMed
    1. Sohl-Dickstein J, Weiss E, Maheswaranathan N et al. Deep unsupervised learning using nonequilibrium thermodynamics. In: Proceedings of the 32nd International Conference on Machine Learning, Vol. 37. JMLR, 2015, 2256–65.

LinkOut - more resources