iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: http://pubmed.ncbi.nlm.nih.gov/28634300/
Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Jul 3;114(27):7049-7054.
doi: 10.1073/pnas.1705642114. Epub 2017 Jun 20.

Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics

Alberto Marin-Gonzalez  1 , J G Vilhena  1   2 , Ruben Perez  3   4 , Fernando Moreno-Herrero  5
Affiliations

Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics

Alberto Marin-Gonzalez et al. Proc Natl Acad Sci U S A. .

Abstract

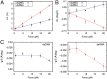
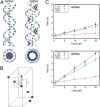
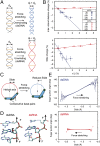
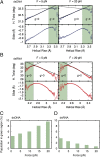
Multiple biological processes involve the stretching of nucleic acids (NAs). Stretching forces induce local changes in the molecule structure, inhibiting or promoting the binding of proteins, which ultimately affects their functionality. Understanding how a force induces changes in the structure of NAs at the atomic level is a challenge. Here, we use all-atom, microsecond-long molecular dynamics to simulate the structure of dsDNA and dsRNA subjected to stretching forces up to 20 pN. We determine all of the elastic constants of dsDNA and dsRNA and provide an explanation for three striking differences in the mechanical response of these two molecules: the threefold softer stretching constant obtained for dsRNA, the opposite twist-stretch coupling, and its nontrivial force dependence. The lower dsRNA stretching resistance is linked to its more open structure, whereas the opposite twist-stretch coupling of both molecules is due to the very different evolution of molecules' interstrand distance with the stretching force. A reduction of this distance leads to overwinding in dsDNA. In contrast, dsRNA is not able to reduce its interstrand distance and can only elongate by unwinding. Interstrand distance is directly correlated with the slide base-pair parameter and its different behavior in dsDNA and dsRNA traced down to changes in the sugar pucker angle of these NAs.

Keywords: DNA; RNA; molecular dynamics; nucleic acid mechanical properties; twist-stretch coupling.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Fig. 1.
Fig. 1.
dsDNA and dsRNA molecules under a constant stretching force. (A) dsDNA and dsRNA molecule starting configurations were B-form DNA and A-form RNA. For both molecules, the force (black arrow) was implemented to act on the centers of mass of the C1′ atoms of the second and 15th base pairs (red). Five simulations of t ≥ 1 μs each were run for each molecule at force moduli of 1, 5, 10, 15, and 20 pN. (B) Computed rmsd values for the heavy atoms of the 10 central base pairs of dsDNA and dsRNA with respect to their standard B- and A-forms at every frame (1,000 steps of 2 fs) of the simulation (gray) and averaged over a running window of 2,000 frames (red).
Fig. 2.
Fig. 2.
Determination of all of the parameters of the elastic rod model from MD data. (A) Relative change in extension of dsDNA (blue) and dsRNA (red) with respect to the extension at F = 1 pN and as a function of the applied force. The extension was computed as the mean value of the helical rises of the 10 central base pairs averaged over the last 0.8 μs (400,000 simulation frames) at each constant force. The linear fits have slopes of (89 ± 4) × 10−5 pN−1 and (240 ± 4) × 10−5 pN−1 for dsDNA and dsRNA, respectively. (B) Absolute change in the twisting angle of dsDNA and dsRNA with respect to the simulation data at F = 1 pN divided by the extension at F = 1 pN plotted as a function of the force. The twisting angle was computed as the mean of the helical twists of the 10 central base pairs averaged over all of the simulation frames. A linear fit was performed, yielding slopes of (3.8 ± 0.3) × 10−3 deg⋅Å−1⋅pN−1 and (−6.2 ± 0.6) × 10−3 deg⋅Å−1⋅pN−1 for dsDNA and dsRNA, respectively. deg, degrees. (C) Ratio −g/S was computed at each constant force simulation as the slope of the linear fit of the helical twist as a function of the helical rise (SI Appendix, Fig. S3). Dashed lines are a guide to the eye. Linear fits in A and B were constrained to pass through the origin point (1,0). Error bars were calculated as described in Materials and Methods.
Fig. 3.
Fig. 3.
Discrete model explains the different stretching response of dsDNA and dsRNA. (A) Top and side views of dsDNA (Left) and dsRNA (Right) molecules. The model is based on the springiness hypothesis (5, 20), where purple beads represent consecutive base-pair centers and form a chain that runs around the helical axis of the molecules. This chain deviates from the helical axis significantly more for dsRNA than for dsDNA. (B) Each segment is characterized by the three parameters h, l, and β, where l is the distance to the next base-pair center, h is the projection of l on the helical axis, and β is the angle defined by these two parameters. The extension can increase by either reducing β (i.e., increasing cos⁡β) and/or increasing l. These values are denoted by xΔβ and xΔl, respectively. At first-order approximation, the total change in extension can be written as x≡Δh=xΔβ+xΔl (SI Appendix). (C) xΔβ/L and xΔl/L contributions to the total relative change in extension x/L (same data as in Fig. 2A) for dsDNA (Upper) and dsRNA (Lower). A linear fit constrained to pass through the origin point (1,0) was carried out for each dataset. From the slopes, we calculated kβ,DNA = 1,330 ± 50 pN, kβ,RNA= 522 ± 3 pN, kl,DNA = 5,600 ± 1,500 pN, and kl,RNA = 2,170 ± 140 pN. Error bars in C were calculated as described in Materials and Methods.
Fig. 4.
Fig. 4.
Physical mechanism of the opposite sign of dsDNA and dsRNA twist-stretch coupling. (A, Upper) Double helical structure can overwind when stretched if the interstrand distance is allowed to shrink. (A, Lower) Alternatively, a fixed interstrand distance duplex will unwind when stretched. (B) Relative change of the interstrand distance (Upper) and slide (Lower) with respect to the F = 1 pN value, plotted against the relative increase in the extension induced by force (dsDNA, blue; dsRNA, red). Datasets were fitted to a linear function constrained to pass through the (0,0) point, excluding the value at F = 20 pN for dsDNA (main text). Error bars were calculated as described in Materials and Methods. (C) Cartoon illustrating the relationship between slide and interstrand distance upon stretching. A reduction of slide is accompanied by a reduction of the interstrand distance as it occurs with dsDNA (SI Appendix, Fig. S8). (D) Representation of two base-pair steps to highlight the different orientation of the sugar with respect to the phosphate backbone of dsDNA (Left) and dsRNA (Right). (E) Fluctuations in sugar pucker angle with respect to the slide parameter. The bin size is 0.02 Å. Data points are mean values with SEM.
Fig. 5.
Fig. 5.
Coupling between twist and slide with helical rise as a function of the force. (A) Fluctuations in helical (H.) twist and slide plotted against helical rise at forces F = 5 pN and F = 20 pN for dsDNA. The helical rise was discretized in bins of 0.02 Å, and the mean value of the slide and the H. twist and helical rise were computed in each bin. Error bars are the SEM of each bin. The green region is defined as a helical rise >3.3 Å for dsDNA. The dashed line is the linear fit of the points in the green region, and the continuous line is the fit to all data points. (B) Fluctuations in H. twist and slide for dsRNA. The green region for dsRNA is defined as a helical rise <2.4 Å. (C) Population in the green region for dsDNA at different forces. (D) Population in the green region for dsRNA at different forces.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bustamante C, Bryant Z, Smith SB. Ten years of tension: Single-molecule DNA mechanics. Nature. 2003;421:423–427. - PubMed
    1. Gore J, et al. DNA overwinds when stretched. Nature. 2006;442:836–839. - PubMed
    1. Lionnet T, Joubaud S, Lavery R, Bensimon D, Croquette V. Wringing out DNA. Phys Rev Lett. 2006;96:178102. - PubMed
    1. Kosikov KM, Gorin AA, Zhurkin VB, Olson WK. DNA stretching and compression: Large-scale simulations of double helical structures. J Mol Biol. 1999;289:1301–1326. - PubMed
    1. Lipfert J, et al. Double-stranded RNA under force and torque: Similarities to and striking differences from double-stranded DNA. Proc Natl Acad Sci USA. 2014;111:15408–15413. - PMC - PubMed

Publication types

LinkOut - more resources