Distribuição normal
Em probabilidade e estatística, a distribuição normal é uma das distribuições de probabilidade mais utilizadas para modelar fenômenos naturais. Isso se deve ao fato de que um grande número de fenômenos naturais apresenta sua distribuição de probabilidade tão proximamente normal, que a ela pode ser com sucesso referida, e, portanto, com adequado acerto por ela representada como se normal fosse[1]. A distribuição normal é ligada a vários conceitos matemáticos como movimento browniano,[2] ruído branco,[3] entre outros. A distribuição normal também é chamada distribuição gaussiana, distribuição de Gauss ou distribuição de Laplace–Gauss, em referência aos matemáticos, físicos e astrônomos francês Pierre–Simon Laplace (1749 – 1827) e alemão Carl Friedrich Gauss (1777 – 1855).[4]
| Distribuição Normal | |
|---|---|
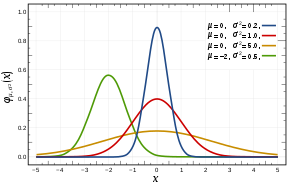 | |
A cor vermelha representa a função de densidade de probabilidade da distribuição normal padrão ~ N(0,1) | |
 | |
A cor vermelha representa a função de distribuição acumulada da distribuição normal padrão ~ N(0,1) | |
| Parâmetros | , média; , variância |
| Suporte | |
| f.d.p. | |
| f.d.a. | |
| Média | |
| Mediana | |
| Moda | |
| Variância | |
| Obliquidade | 0 |
| Curtose | 0 |
| Entropia | |
| Função Geradora de Momentos | |
| Função Característica | |

Em termos mais formais, a distribuição normal é uma distribuição de probabilidade absolutamente contínua parametrizada pela sua esperança matemática (número real ) e desvio padrão (número real positivo ). A densidade de probabilidade da distribuição normal é denotada como
- .
A distribuição normal com média nula e desvio padrão unitário é chamada de distribuição normal centrada e reduzida ou de distribuição normal padrão. Quando uma variável aleatória segue uma distribuição normal, ela é chamada de gaussiana ou de normal. Comumente é usada a notação com a variância quando A curva de densidade é chamada de curva de Gauss ou de curva em forma de sino.[5]
O papel central da distribuição normal decorre do fato de ser o limite de um grande número de distribuições de probabilidade como mostra o teorema central do limite, o qual permite estudar probabilisticamente a média das variáveis independentes de uma amostra aleatória simples de tamanho grande .[6] A distribuição normal corresponde ao comportamento do efeito agregado de experiências aleatórias independentes e semelhantes em certas circunstâncias quando o número de experiências é muito alto.[7] Com esta propriedade, a distribuição normal pode aproximar–se da distribuição de efeito agregado de outras distribuições e modelar vários estudos científicos como erros de medição ou testes estatísticos com as tabelas de distribuição normal.[8]
Histórico
editarUma das primeiras aparições da distribuição normal ocorreu em 1733 com Abraham de Moivre com o aprofundamento do estudo de fatorial quando considerado um jogo de cara ou coroa.[9] Em 1756, ele publicou A Doutrina das Chances, em que a distribuição normal aparece como o limite de uma distribuição binomial, o que originaria o teorema central do limite.[10]
Em 1777, Pierre-Simon Laplace retomou o trabalho e obteve uma boa aproximação do erro entre a distribuição normal e a distribuição binomial em razão da função gama de Euler.[9] Em seu livro publicado em 1781, Laplace publica uma primeira tabela da distribuição normal. Em 1809, Carl Friedrich Gauss assimila os erros da observação na astronomia à curva, erros da densidade da distribuição normal.[10]
A distribuição normal é totalmente definida quando o primeiro teorema central do limite (chamado então teorema de Laplace) é elaborado por Laplace em 1821.[10] O nome normal é dado por Henri Poincaré no fim do século XIX.[11] A distribuição normal também pode ser chamada de distribuição de Gauss ou distribuição de Laplace–Gauss,[12] de acordo com sua autoria. A denominação segunda distribuição de Laplace também é usada ocasionalmente.[13][14]
A distribuição normal é estudada frequentemente. Por exemplo, novas tabelas digitais foram publicadas por Egon Sharpe Pearson em 1948, pelo National Bureau of Standards em 1952 e por Greenwood e Hartley em 1958.[15][16]
Distribuição normal padrão
editarExiste uma infinidade de distribuições normais, cada uma com sua própria média e desvio padrão. A distribuição normal com média 0 e desvio padrão 1 é chamada de distribuição normal padrão.[17] Ela é uma distribuição de probabilidade (uma medida , de massa total unitária) unidimensional (com suporte real ).[18] É uma distribuição absolutamente contínua (a medida é absolutamente contínua em relação à medida de Lebesgue).
Em outras palavras, existe uma densidade de probabilidade muitas vezes denotada como para a distribuição normal padrão tal que: . É generalizada para a distribuição normal multivariada. A distribuição normal padrão também pode ser chamada de distribuição normal centrada e reduzida.[19] A escala horizontal do gráfico da distribuição normal padrão corresponde ao escore-z que é uma medida de posição que indica o número de desvios padrão em que um valor se encontra a partir da média. Podemos transformar um valor em escore-z usando a fórmula:
Arredondar para o centésimo mais próximo
Quando um valor de uma variável aleatória distribuída normalmente é transformado em um escore-z, a distribuição de será uma distribuição normal padrão. Após essa transformação, a área que recai no intervalo sob a curva normal padrão é a mesma que aquela sob a curva normal padrão no correspondente intervalo .[20]
Propriedades da distribuição normal padrão
editar- A área acumulada é próxima de 0 para escores-z próximos a z=-3,49.
- A área acumulada aumenta conforme os escores-z aumentam.
- A área acumulada para z=0 é 0,5000.
- A área acumulada é próxima a 1 para escores-z próximos a z=3,49.
Definição pela função densidade
editarA densidade da distribuição normal padrão é dada pela função definida por , para todo .[21] Esta distribuição é chamada centrada porque o valor do seu momento de ordem 1 (esperança) é 0 e reduzida porque o valor do seu momento de ordem 2 (variância) é 1, assim como o seu desvio padrão. O gráfico da densidade é chamado função gaussiana, curva de Gauss ou curva em forma de
sino. A distribuição normal é denotada pela letra . Uma variável aleatória que segue uma distribuição normal padrão é denotada como .[22]
Seguem algumas propriedades sobre a função densidade:
- O cálculo da integral de Gauss permite demonstrar que a função é uma densidade de probabilidade pela fórmula .
- É contínua, uniformemente limitada e par.[23]
- O máximo da função é atingido na média 0 e de valor .[23]
- Verifica .[24]
- A densidade é infinitamente derivável. Uma indução matemática permite obter a fórmula para a -ésima derivada de : , em que é o –ésimo polinômio de Hermite.[25]
- A densidade possui dois pontos de inflexão, em 1 e em –1. Estes são os pontos em que a segunda derivada se anula e muda de sinal. Os dois pontos são aproximadamente três quintos da altura total.[18]
Definição pela função distribuição
editarHistoricamente a distribuição normal aparece como a distribuição limite no teorema central do limite, usando a função de distribuição cumulativa. A distribuição normal é a distribuição de probabilidade, em que a função de distribuição é dada por , definida por
, para todo . Ela fornece a probabilidade de uma variável aleatória de distribuição normal pertencer a
um intervalo fechado , .[26]
Seguem algumas propriedades sobre a função de distribuição:
- Não existe uma expressão analítica para a função de distribuição . Isto é, não é expressa a partir de funções usuais, mas torna–se uma função usual. Para obter os valores de probabilidade é preciso aproximar esta função de outras funções usuais gerando a tabela de valores.[27]
- Pode ser expressa em função da função erro por meio das seguintes fórmulas equivalentes e .[28]
- É infinitamente derivável e verifica . A fórmula equivalente permite definir a integral de Lebesgue–Stieltjes com relação à distribuição normal.[29]
- É absolutamente contínua e estritamente crescente, sendo uma bijeção de no intervalo aberto .[30] O recíproco é chamado de função inversa da função distribuição acumulada da distribuição normal. Por exemplo, esta função é utilizada pelo modelo probit.[31]
- Pela paridade da distribuição, . Portanto, . Isso mostra que a mediana da distribuição normal padrão é 0.[30]
Definição pela função característica
editarA caracterização da distribuição normal pela função característica tem o objetivo de demonstrar certas propriedades como a estabilidade da soma e o teorema central do limite. A função característica de distribuição normal padrão é dada por
e definida por , para todo .[32][33] Em grego existem duas variações para a letra phi minúscula. O utilizado agora é diferente do utilizado no início do texto. Isto é, são duas notações diferentes para phi minúsculo.
Esta função característica é proporcional à densidade da distribuição padrão. Ela permite demonstrar certas propriedades como a estabilidade por adição e o teorema central do limite.[34]
Seguem algumas propriedades sobre a função de distribuição:
- A função característica da distribuição normal pode ser obtida a partir da função densidade pelas igualdades .[26]
- Se uma variável aleatória segue uma distribuição normal padrão da função característica definida acima, então a transformação linear admite a função característica . É uma variável aleatória com distribuição normal de média e variância .[35]
Definição pela função geradora de momentos
editarUma outra maneira de definir a distribuição normal padrão é pela utilização da função geradora de momentos. É a distribuição de probabilidade, em que a função geradora de momentos é dada por e definida por[36] , para todo . O objetivo é calcular os momentos da distribuição normal.[37]
Seguem algumas propriedades sobre a função geradora de momentos:
- A função geradora de momentos da distribuição normal pode ser obtida a partir da função densidade. Seja , que segue uma distribuição normal padrão, então .[36]
- Se uma variável aleatória segue uma distribuição normal padrão da função geradora de momentos , então a transformação linear admite a função geradora de momentos . Assim, é uma variável aleatória com distribuição normal de média e variância .[37]
Distribuição normal geral
editarDefinição
editarMais usualmente que a distribuição normal padrão, a distribuição normal não centrada e não reduzida é a distribuição de probabilidade absolutamente contínua, na qual um dos quatros pontos seguintes podem ser verificados.
- A densidade de probabilidade é dada pela função , definida por , para todo .[21]
- A função de distribuição (cumulativa) é dada pela função , definida por , para todo .[38]
- A função característica é dada por , definida por , para todo .[33]
- A função geradora de momentos é dada por , definida por , para todo ou e .[39]
Para , as funções de densidade e de distribuição não são definidas. Este caso corresponde a um comportamento degenerado da distribuição normal, às vezes chamada de distribuição normal imprópria. Isto é a medida de Dirac no ponto . O valor é a média da distribuição, é o desvio padrão e é a variância. Esta distribuição é denotada por , uma variável aleatória que segue a distribuição normal com a média e variância é denotada por .[33]
Observações
editar- Se a variável aleatória segue uma distribuição normal padrão , então a variável aleatória segue uma distribuição normal de média e de variância . Reciprocamente, se segue uma distribuição normal , então segue uma distribuição normal padrão.[40] Em outras palavras, toda distribuição normal pode ser obtida pela translação e pela dilatação de uma distribuição normal padrão. Esta primeira propriedade permite obter a fórmula .[41] Então, é possível deduzir as propriedades da distribuição normal a partir da distribuição normal centrada reduzida e vice–versa. A variável às vezes é chamada de padronização de ou de variável padrão .[42]
- A densidade é simétrica em relação à .[23]
- O máximo da função é atingido em , com valor .[23]
- Desde que a distribuição normal seja uma distribuição de probabilidade absolutamente contínua, o evento é insifgnificante. Isto é, quase certamente uma variável aleatória com distribuição normal nunca é igual a um valor fixo . Isto é expresso matematicamente por .[43]
- A largura à meia altura (largura da curva à metade da altura total) fornece um valor da amplitude da distribuição. Esta largura à meia altura da distribuição normal é proporcional ao desvio padrão . O fator 2 vem da propriedade de simetria da distribuição normal.[44]
- A densidade tem dois pontos de inflexão, em e em . Eles são os pontos, nos quais a segunda derivada anula–se e muda de sinal. Os dois pontos situam–se aproximadamente três quintos da altura total.[18]
- A distribuição normal é uma distribuição da família exponencial. Isto é, a sua densidade é escrita como ou como , com , , e .[45]
Propriedades
editarOutras caracterizações
editarEm adição à densidade de probabilidade, à função de distribuição, à função característica e à função geradora de momentos, existem outras caracterizações da distribuição normal.
- Caracterização segundo Georges Darmois e Sergeï Bernstein – se duas variáveis aleatórias e são independentes e igualmente distribuídas e se duas variáveis aleatórias e também são independentes, então a distribuição comum e é a distribuição normal.[10]
- Caracterização segundo Charles Stein – a distribuição normal é a única distribuição de probabilidade (medida de probabilidade) tal qual, para qualquer função de classe C¹ (derivável ou derivada contínua), [18]
Momentos
editarO momento de ordem 1 é chamado média ( ) e é dado como parâmetro da distribuição normal . O segundo parâmetro é o desvio padrão ( ). Isto é, a raiz quadrada da variância , que é, por definição, a média dos quadrados dos desvios da média, ou segundo momento central. Os momentos centrais da distribuição normal são dados por ,
para e uma variável aleatória com distribuição normal .[37]
O momento central de ordem pode ser obtido a partir de uma função de momentos de ordem inferior à e o momento de ordem pode ser obtido a partir de momentos de ordem inferior à – 1 e do momento central de ordem . Então, os primeiros momentos da distribuição normal são:
.[46]
Cálculo
editarCom a simetria em torno de da função densidade da distribuição normal, os momentos centrais de ordem ímpar são todos zero.[47] Os momentos de ordem par da distribuição normal padrão pode ser obtido pela relação de recorrência , que vem da integração por partes seguinte, para , .[48]
É deduzida a fórmula dos momentos centrais reduzidos , assim a fórmula dos momentos centrais .[26]
Função geradora de momentos
editarOs momentos centrais de uma distribuição podem ser obtidos a partir da função geradora de momentos centrados. Para a distribuição , a mudança da variável permite obter as fórmulas de uma parte e de outra parte.[37]
Para a identificação dos coeficientes das duas séries, isto implica que os momentos de ordem ímpar são zero e fornece uma fórmula para os momentos de ordem par .[26]
Assimetria e curtose
editarDensidades de probabilidade de distribuições com curtoses diferentes. Em vermelho, a distribuição de Laplace. Em laranja, a distribuição secante hiperbólica. Em verde, a distribuição logística. Em preto, a distribuição normal. Em cinza, a loi du cosinus surélevé. Em azul, a loi du demi-cercle. Em violeta, a distribuição uniforme.
A assimetria , a curtose e a curtose normalizada são obtidas a partir das fórmulas dos momentos .[49]
A distribuição normal é um ponto de referência para comparação das espessuras de caudas longas. Se uma distribuição possui uma curtose normalizada , então a distribuição possui uma cauda longa mais grossa que a distribuição normal e é chamada leptocúrtica. Se , a distribuição possui uma cauda longa mais fina que a distribuição normal e é chamada platicúrtica. Se a distribuição possui uma curtose normalizada nula, então a distribuição possui uma cauda longa comparável à distribuição normal e é chamada mesocúrtica.[50][51]
- Cumulantes
A função característica permite obter a função geradora de cumulantes pela fórmula e permite obter os cumulantes , e , para .[52]
Teoremas da convergência
editarA primeira versão do teorema central do limite (teorema de Moivre–Laplace) foi estabelecido para as variáveis aleatórias da distribuição de Bernoulli. De maneira mais geral, se são variáveis aleatórias independentes e igualmente distribuídas com variância finita e se a soma é denotada como , então , para todo , em que é a densidade de probabilidade da distribuição normal padrão.[27]
Este teorema significa que tudo que pode ser considerado a soma de um grande número de pequenos valores aleatórios independentes aproxima–se de uma distribuição normal.[53] Isto mostra a característica central da distribuição normal, em teoria da probabilidade. Um enunciado do teorema pode ser formulado como: se uma grandeza física submetida à influência de um número importante de fatores independentes e se a influência de cada fator separadamente é pequena, então a distribuição desta grandeza é uma distribuição gaussiana.[54]
O teorema central do limite é válido para toda distribuição de probabilidade com variáveis independentes e identicamente distribuídas que, com desvio padrão finito, permite obter uma boa aproximação da soma . Por exemplo,
- se as variáveis seguem a distribuição de Bernoulli , então segue aproximadamente uma distribuição normal . Esta aproximação é satisfatória quando ;[55]
- se as variáveis seguem a distribuição qui–quadrado com um graus de liberdade , então segue aproximadamente uma distribuição normal ;[56]
- se as variáveis seguem a distribuição exponencial , então segue aproximadamente uma distribuição normal .[57]
Existem versões mais gerais deste teorema. Por exemplo, variáveis aleatórias independentes não são da mesma distribuição, mas com pequenas variâncias em relação às suas médias.[58] Um teorema de Gnedenko e Kolmogorov (1954) estipula que uma variável aleatória normal é a soma de um grande número de variáveis aleatórias indenpendentes pequenas , sendo que nenhuma delas é predominante.[59]
Teorema – Seja uma série de variáveis aleatórias , sendo que cada uma é a soma de um número finito de variáveis aleatórias com . Para todo , introduz–se a variável aleatória truncada e supõe–se
Então, a distribuição de converge para a distribuição normal .[62]
Estabilidade e família normal
editar- Estabilidade pela adição (propriedade de conservação)
A distribuição normal é estável pela adição. Isto é, a soma de duas variáveis aleatórias independentes com distribuição normal é em si uma variável aleatória com distribuição normal. Mais explicitamente, se , e e são independentes, então a variável aleatória segue a distribuição normal .[10]
Esta propriedade é generalizada por variáveis, isto é, se para todo as variáveis aleatórias seguem a distribuição normal e são independentes, então a soma segue a distribuição normal .[63]
Esta propriedade é demonstrada diretamente por meio de funções características. A densidade de probabilidade da soma de duas variáveis aleatórias independentes da distribuição normal é dada pela convolução de duas densidades. Isto é traduzido pelas fórmulas de convolução de funções: ,[64]
ou de convolução de medidas normais denotadas como : . Não deve ser confundida com a distribuição, cuja densidade é a soma das densidades da distribuição normal.
Família normal
editarO conjunto de funções forma a chamada "família normal", que por sua vez também é o nome do conjunto de distribuições normais .[65] A família de funções está fechada para convolução no sentido que a função gera a família. Toda densidade que convolui um número suficientemente grande de vezes e adequadamente renormalizada está próxima de uma função de uma família normal.[64]
Os seguintes teoremas dão mais detalhes matemáticos:
- Se para uma função de densidade de média 0 e desvio padrão 1, e quaisquer e existe e , satisfazendo , então é a densidade da distribuição normal padrão.[66]
- De acordo com o teorema de Lévy–Cramér (1936), conjecturado por Paul Lévy, em 1935, se duas funções de densidade e verificam , então e com e . Em outras palavras, se a soma de duas variáveis aleatórias independentes é normal, então as duas variáveis aleatórias seguem a distribuição normal.[10][67]
- Se é a densidade comum de variáveis aleatórias independentes de média 0 e desvio padrão 1, então a convolução vezes de converge uniformemente em : (este teorema é equivalente ao teorema central do limite). Esta família normal não deve ser confundida com a família normal de funções holomorfas[64]
Estabilidade por linearidade
editarA distribuição normal é estável por linearidade. Se e são reais e , então a variável aleatória segue a distribuição normal .[68] Com a estabilidade por adição e por linearidade, a distribuição normal é um caso particular de distribuição estável com parâmetro de estabilidade .[69] Entre as distribuições estáveis, a distribuição normal, a distribuição de Lévy ( ) e a distribuição de Cauchy ( ) são as únicas com expressão analítica para a função densidade.[70]
Estabilidade pela média
editarA distribuição normal é estável pela média. Se são variáveis aleatórias independentes seguindo as distribuições normais , então a média segue a distribuição [71]
Convexidade
editarA distribuição normal não é convexa.[72] Isto é, a desigualdade , para todo e borelianos, não é satisfeita quando a medida é normal. Entretanto, quando a desigualdade é normalizada com o inverso da função de distribuição da distribuição normal padrão, obtém–se o teorema (desigualdade de Ehrhard) , para a medida padrão normal , todos os intervalos e e todo .[73]
Entropia e quantidade de informação
editarEntropia de Shannon
editarA entropia de Shannon de uma distribuição de probabilidade absolutamente contínua de densidade dada por para medir a quantidade de informação é definida por No conjuntos das distribuições absolutamente contínuas de variância fixa, as distribuições normais fornece entropia máxima.[74] A entropia para uma distribuição normal é dada por . Há também uma ligação entre a convergência de sequências de distribuições de probabilidade com distribuição normal e o aumento da entropia, tornando–se uma ferramenta importante na teoria da informação.[10]
Quantidade de informação de Fisher
editarA informação de Fisher de uma densidade de probabilidade é outro conceito de quantidade de informação. Para uma densidade , a informação de Fisher é dada por Para toda densidade suficientemente regular de uma distribuição normal padrão, a informação satisfaz a seguinte desigualdade: . A distribuição normal distingui–se de outras densidades desde que a desigualdade anterior seja uma igualdade e se e somente se a densidade for uma distribuição normal padrão.[10]
Distancia entre distribuições
editarA divergência de Kullback–Leibler permite medir a distância entre duas distribuições ou a perda de informação entre as duas distribuições. A divergência de Kullback–Leibler entre as duas distribuições normais e é .
Esta divergência é nula para e , mas aumenta quando também aumenta.[75]
Aproximação da função de distribuição
editarNão existe expressão analítica para a função de distribuição da distribuição normal padrão. Isto é, não existe uma fórmula simples entre a função de distribuição e as funções convencionais como as funções polinomiais, exponenciais, logarítmicas, trigonométricas, entre outras. Entretanto, a função de distribuição é aplicada a vários resultados e é importante compreende–la melhor. Diferentes notações como séries ou frações contínuas generalizadas são possíveis.[76]
Para , a função de distribuição da distribuição normal padrão é escrita na forma ou na forma [44]
Para , a função de distribuição da distribuição normal padrão é escrita na forma
De maneira mais numérica e facilmente calculável, as aproximações seguintes fornecem valores da função de distribuição da distribuição normal padrão com:
Em um exemplo de algoritmo para a linguagem C, uma outra notação da função de distribuição da distribuição normal padrão utiliza uma fração contínua generalizada: .[28]
Tabelas numéricas e cálculos
editarDe acordo com a seção anterior, é útil saber a função de distribuição para aplicações numéricas. Então, tabelas de valores foram calculadas para a função de distribuição e também para o inverso da função de distribuição, que permitem obter os quantis e os intervalos de confiança para um limiar de tolerância fixo.[78]
Tabela de valores dos quantis
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| As duas tabelas seguintes fornecem os valores dos quantis da distribuição normal padrão , definida por .[79]
Os valores da primeira linha fornecem a primeira parte da variável. Os valores da primeira coluna fornecem a segunda parte da variável. Então, a célula na segunda linha e na terceira coluna fornece .
Esta tabela fornece os valores dos quantis para os valores maiores de .
|
As tabelas são dadas pelos valores positivos da distribuição normal padrão. Com a formulação da função de distribuição, é possível obter outros valores. Os valores negativos da função de distribuição são dados pela fórmula . Por exemplo, , para .[16]
Os valores da função de distribuição da distribuição geral é obtido pela fórmula .[80] Por exemplo, , para .[81]
A tabela de valores também permite obter a probabilidade de uma variável aleatória com distribuição normal pertencer a um intervalo pela fórmula . Por exemplo, , para , e , para .[82]
Intervalos normais e intervalos de confiança
editarUma das vantagens para calcular probabilidades de intervalos é a utilização de intervalos de confiança para testes estatísticos. A distribuição normal é definida para dois valores, a média e o desvio padrão . É útil olhar para os intervalos do tipo:
. para . [83]
Tabela de valores dos intervalos de confiança
| ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
A tabela seguinte é obtida a partir das tabelas anteriores e fornecem as probabilidades para [84]
|
A tabela de valores dos valores de confiança permite obter os intervalos de normalidade para um determinado nível de confiança. Para , a tabela fornece:
- , em que é o intervalo de normalidade para o nível de confiança de 68%.[85]
- , em que é o intervalo de normalidade para o nível de confiança de 76% e é a largura à meia altura.[85]
- , em que é o intervalo de normalidade para o nível de confiança de 95%.[85]
- , em que é o intervalo de normalidade para o nível de confiança de 99%.[85]
Inversamente, quando o valor da probabilidade é fixo, existe um único valor , tal que .[30] O intervalo é chamado de intervalo de normalidade ou intervalo de confiança para o nível de confiança . Para uma distribuição normal e um limiar , o método para encontrar o valor de consiste em utilizar a tabela de valores dos quantis, tal que .
Então, o intervalo de confiança é . Por exemplo, o intervalo de normalidade para o nível de confiança de 95% de uma distribuição normal é o intervalo , em que verifica ou .
Então, o intervalo de confiança é após o arredondamento.[86]
Ligações com outra distribuições
editarCom papel central entre as distribuições de probabilidade e suas aplicações, a distribuição normal tem muitas ligações com outras distribuições. Certas distribuições ainda são formadas a partir da distribuição normal para melhor corresponder às suas aplicações.[87]
Distribuições usuais
editar| Distribuição | Em função de variáveis com distribuição normal |
|---|---|
| Distribuição qui–quadrado | [88] |
| Distribuição qui–quadrado não central | [89] |
| Distribuição qui | |
| Distribuição qui não central |
Distribuições unidimensionais
editar- Se uma variável aleatória segue uma distribuição normal , então a variável aleatória segue uma distribuição log–normal.[90]
- Se e são duas variáveis aleatórias independentes com distribuição uniforme , então as duas variáveis aleatórias e são distribuições normais padrões. e são independentes. Estas duas fórmulas são utilizadas para simular a distribuição normal.[80]
- Se as variáveis são independentes com distribuição comum , então a soma dos seus quadrados segue uma distribuição qui–quadrado com grais de liberdade . A formula estende–se para variáveis normal não centradas e não reduzidas. O mesmo tipo de ligação existe com a distribuição qui–quadrado não central, a distribuição qui e a distribuição qui não central.[91]
- Se a variável segue uma distribuição normal padrão , se segue uma distribuição qui–quadrado com grais de liberdade e se e são independentes, então a variável segue uma distribuição de Student com grais de liberdade.[92]
- Se é uma variável aleatória com distribuição normal padrão e é uma variável aleatória com distribuição uniforme em , então é uma distribuição de Slash.[93]
- Para uma variável aleatória com distribuição normal padrão , a variável é um distribuição normal com potência . Para , esta variável é uma distribuição normal padrão.[93]
- Se e são duas variáveis aleatórias independentes com distribuição normal padrão, então o quociente segue a distribuição de Cauchy de parâmetro 0 e 1, .[94] No caso de e serem duas gaussianas quaisquer (não centradas e não reduzidas), o quociente segue uma distribuição complexa, em que a densidade é expressa em função dos polinômios de Hermite (a expressão exata é dada por Pham–Gia em 2006).[95]
Distribuições multidimensionais
editar- Há uma versão multidimensional da distribuição normal, chamada distribuição normal multidimensional, distribuição multinormal ou distribuição de Gauss multivariada. Se são variáveis aleatórias com distribuições normais, então a distribuição de probabilidade do vetor aleatório é uma distribuição normal multidimensional. A densidade de probabilidade assume a mesma forma que a densidade da distribuição normal, porém escrita em forma de matriz. Se o vetor aleatório tem distribuição normal unidimensional , em que é o vetor das médias e é a matriz de variância–covariância, então a distribuição condicional de , sabendo que é a distribuição normal e , então com e [96]
- A distribuição normal de um vetor, cujas coordenas são independentes e com distribuições normais padrão, é a distribuição de Rayleigh.[95]
Nota–se que a distribuição gaussiana inversa e a distribuição gaussiana inversa generalizada não têm ligação com uma fórmula simplesmente criada a partir de variáveis da distribuição normal, mas tem relação com o movimento browniano.[97]
Distribuições normais generalizadas
editarVárias generalizações da distribuição normal foram introduzidas para mudar sua forma, sua assimetria, seu suporte, entre outros. Um novo parâmetro de forma foi introduzido à distribuição normal para obter uma distribuição normal generalizada. Esta família de distribuição contém a distribuição normal como é o caso para e também para a distribuição de Laplace para . A nova densidade de probabilidade é dada por [10]
Existe uma maneira de mudar a assimetria da distribuição normal a fim de obter a chamada distribuição normal assimétrica (distribuição normal distorcida).[98] A introdução de um parâmetro permite obter a distribuição normal quando , uma assimetria à direita quando e uma assimetria à esquerda quando . A densidade desta distribuição é dada por .[99]
Para mudar o suporte e, especialmente, para tornar a distribuição normal limitada, uma modificação possível é a distribuição truncada. Então, ela muda de escala para que as partes cortadas distribuam–se entre todos os valores guardados (ao contrário da distribuição dobrada). A distribuição normal padrão truncada em e em para suportar o intervalo e sua função densidade definida por [100]
Também é possível truncar a distribuição normal de um lado. Então, ela é chamada distribuição normal corrigida. Se uma variável aleatória segue uma distribuição normal , então segue a distribuição normal corrigida.[101]
Uma outra maneira de mudar o suporte da distribuição normal é dobrar a densidade a partir de uma valor, a distribuição obtida é a distribuição normal dobrada. Os valores retirados, por exemplo, são então distribuídos perto do valor da dobra, aqui, 0 (ao contrário da distribuição truncada). A densidade de probabilidade da distribuição normal dobrada em 0 é dada por [102]
Uma versão generalizada da distribuição log–normal permite obter uma família com distribuição, incluindo a distribuição normal como um caso particular.[103] A família é definida a partir de três parâmetros: um parâmetro de posição , um parâmetro de escala e um parâmetro de forma . Quando , esta distribuição log–normal generalizada é a distribuição normal. A densidade é dada por , em que .[104]
-
Diferentes formas para a densidade da distribuição normal generalizada.
-
Diferentes formas para a densidade da distribuição normal assimétrica.
-
Diferentes formas para a densidade da distribuição log–normal.
-
Distribuição normal padrão truncada em 1,5 para a curva vermelha e em 2,5 para a curva azul.
-
Em verde, a densidade da distribuição normal dobrada em 0.
Construções a partir da distribuição normal
editarMisturando as distribuições
editarUma mistura gaussiana é uma distribuição de probabilidade, cuja densidade é definida por uma combinação linear de duas densidades de distribuições normais. Se nota–se a densidade de e a densidade de , então é a densidade de uma distribuição de probabilidade chamada de mistura gaussiana.[105]
Os modos das duas distribuições normais são dados por e , então a combinação gaussiana é uma distribuição bimodal. Se os máximos locais são valores próximos e não iguais aos valores e .[105]
Generalidades
editarÉ possível construir outras densidades de probabilidade com a densidade da distribuição normal padrão. Harald Cramér estabeleceu em 1926 um resultado geral: se uma densidade de probabilidade é duas vezes diferenciável, se a integral é convergente e se , então a função pode ser desenvolvida em uma série absolutamente e uniformemente convergente em função das derivadas das densidades da distribuição normal padrão e dos polinômios de Hermite [106]
Utilizações
editarHistoricamente a distribuição normal é introduzida em estudos sobre os corpos celestes ou em jogos de azar. Ela é estudada, generalizada matematicamente e usada em muitas aplicações em matemática, em outras ciências exatas, em outras ciências mais aplicadas ou em ciências humanas e sociais.[107] Segue uma seleção de exemplos.
Balística
editarNo século XIX, para melhorar a precisão da artilharia de fogo muitos tiros de canhão eram disparados. Observou–se que a direção e o alcance eram semelhantes às distribuições normais.[108] Esta compreensão permitiu melhor treinar os servos para ajustar os disparos. Esta distribuição normal proveniente de diferentes fatores como as condições climáticas e também o uso do equipamento militar. A dispersão dos pontos de impacto e, portanto, da distribuição, fornece informações sobre o estado do material e sobre o possível número de disparos anormais. O ajuste à distribuição normal é feito pelo teste de Lhoste em uma série de 200 tiros. O matemático Jules Haag aplica o método para 2 680 tiros de diferentes escopos e diferentes direções.[108]
Quociente de inteligência
editarO quociente de inteligência (QI) visa dar um valor numérico à inteligência humana. Em 1939, David Wechsler deu uma definição estatística ao quociente de inteligência. 100 pontos são dados à média dos valores obtidos de uma população com idade similar e 15 pontos são deduzidos de um intervalo igual ao desvio padrão obtidos a partir dos valores da população testada.[109] Por esta razão, a curva de distribuição do QI é modelada a curva em forma de sino da distribuição normal padrão em 100 e com desvio padrão 15, . Entretanto, este modelo é questionado por alguns cientistas. Em efeito, os resultados dos testes são dependentes das classes sociais da população, a população deixaria de ser homogênea. Isto é, a propriedade de independência dos indivíduos não seria verificada. Então, o QI seria apenas uma medida de aproximação da inteligência humana com erro desconhecido.[110]
Anatomia humana
editarUma característica observável e mensurável de uma população de indivíduos comparáveis muitas vezes tem uma frequência modelada por uma distribuição normal. É o exemplo da altura humana em uma determinada idade (separados entre homens e mulheres)[111] ou o tamanho do bico de uma população de aves como os pássaros estudados por Charles Darwin.[112] Mais precisamente, uma característica mensurável de uma população pode ser modelada por uma distribuição normal se ela for codificada geneticamente por vários alelos ou por vários locus[112] ou se a característica depende de um grande número de efeitos do meio ambiente.[113]
As curvas de crescimento apresentadas pela Organização Mundial da Saúde (OMS), presentes em cadernetas de saúde, por exemplo, são derivadas de modelagem pela distribuição normal. Por meio de um estudo detalhado dos percentis medidos em uma população com idade fixa e por meio de testes estatísticos de adequação, as distribuições dos pesos e das alturas por faixa etária foram modeladas por distribuições de probabilidade. Estas distribuições incluem a distribuição normal, a distribuição normal de Box–Cox (generalização da distribuição normal), a distribuição Student de Box–Cox (generalização da distribuição normal de Box–Cox) e ainda a distribuição exponencial com potência Box–Cox. Graficamente, para cada idade ou para cada eixo vertical, a mediana é representada (linha central) e os dois valores de e , em que é o desvio padrão, dão as curvas e, assim, representam a evolução de um intervalo de confiança.[114]
Sinais e medições físicas
editarQuando um sinal é transmitido, ocorre uma perda de informação devido aos meios de transmissão ou à decodificação do sinal. Quando uma medição física é efetuada, uma incerteza no resultado pode ser proveniente de uma imprecisão do aparelho de medida ou de uma incapacidade de obter o valor teórico. Um método para modelar tais fenômenos é considerar um modelo determinista (não aleatório) para o sinal ou para a medição e adicionar ou multiplicar um termo aleatório que represente a perturbação aleatória, às vezes chamadas de erro ou de ruído. Em muitos casos, este erro é assumido como distribuição normal ou como distribuição log–normal em casos de multiplicação.[115] É o caso, por exemplo, da transmissão de um sinal através de um cabo elétrico.[42] Quando o processo depende do tempo, o sinal ou a medição é modelada por um ruído branco. Então, a suavização de imagem com um filtro gaussiano é utilizada.[116]
Economia
editarOs preços de algumas commodities são determinadas por uma bolsa de valores, como é o caso do trigo, do algodão e do ouro. No tempo , o preço evolui até o momento , aumentando . Em 1900, Louis Bachelier postulou que este aumento segue uma distribuição normal de média nula, cuja variância depende de em . Entretanto, este modelo satisfaz apenas ao mercado financeiro. Então, outros matemáticos propuseram melhorar este modelo, assumindo que é o aumento que segue a distribuição normal, o que quer dizer que o aumento dos preços segue uma distribuição log–normal. Esta hipótese é a base do modelo e da fórmula de Black–Scholes utilizado massivamente pela indústria financeira.[117]
Este modelo ainda foi melhorado por Benoît Mandelbrot especialmente, assumindo que o aumento segue uma distribuição estável (a distribuição normal é um caso particular da distribuição estável). Então, parece que o movimento browniano, cujo crescimento é uma distribuição normal, e o processo de Levy, cujo crescimento estável modela as curvas do mercado.[117]
Matemática
editarA distribuição normal é utilizada em muitas áreas da matemática. O ruído branco gaussiano é um processo estocástico de tal modo que em qualquer ponto o processo é uma variável aleatória com distribuição normal independente do processo de outros pontos.[118] O movimento browniano é um processo estocástico, cujos aumentos são independentes, estacionários e com distribuição normal.[117] Incluindo um valor fixo, a variável aleatória segue a distribuição normal . Este processo aleatório tem muitas aplicações. Ele faz uma ligação entre a equação do calor e a distribuição normal.[18] Quando a extremidade de uma haste de metal é aquecida em um curto espaço de tempo, o calor se propaga ao longo da barra na forma de uma curva em forma de sino.
A distribuição normal também é aplicada em áreas da matemática não aleatórias como na teoria dos números. Todo número inteiro pode ser escrito como a multiplicação de potências de números primos. Seja o número de números primos diferentes nesta decomposição. Por exemplo, para , . O teorema de Erdős–Kac assegura que esta função para está relacionada com a densidade da distribuição normal . Isto é, para um grande número da ordem de , existe uma alta probabilidade que o número de divisores primos seja 3 para .[18]
Testes e estimativas
editarCritérios de normalidade
editarÉ importante saber se os valores são distribuídos de acordo com a distribuição normal. Quatro critérios podem ser estudados antes de realizar um teste estatístico.
O primeiro critério (o critério mais simples) consiste em traçar um diagrama em barras da distribuição e verificar visualmente se o diagrama é em forma de sino. Entretanto, este critério subjetivo permite eliminar uma parte das distribuições quando consideradas não gaussianas.[119]
De maneira mais precisa, a utilização das faixas de normalidade permite comparar com as frequências observadas facilmente calculáveis. O critério consiste em utilizar as faixas de normalidade ou os intervalos de confiança. Quando os valores são normalmente distribuídos, 68% deles estão no intervalo , 95% deles estão no intervalo e 99,7% deles estão no intervalo .[120]
Se não for o caso, a escolha de modelar a distribuição dos valores observados pela distribuição normal não é aconselhável.
O gráfico de probabilidade normal permite ajustar os valores observados com uma distribuição normal. Isto é, representando o gráfico de probabilidade normal, é possível fazer um diagnóstico sobre a natureza normal da distribuição e, se ela for susceptível a ser normal, é possível determinar a média e o desvio padrão. Os valores são observados e representados pela função de distribuição empírica . Elas são gaussianas se os pontos representados no papel gráfico gaussiano-aritmético estão alinhados em uma reta chamada Henri.[121] Um papel gaussiano-aritmético é formado por um eixo aritmético das abscissa e é calculada pelo inverso da função de distribuição da distribuição normal padrão de ordem .[122]
Estes critérios são necessários, mas não são suficientes para afirmar que os valores são normalmente distribuídos.[123]
Testes de normalidade
editarCom seu papel no teorema central do limite, a distribuição normal é encontrada em muitos dos testes estatísticos chamados gaussianos ou assintoticamente gaussianos. O pressuposto de normalidade é feito sobre uma distribuição a priori em um teste de aderência para indicar que esta distribuição segue aproximadamente uma distribuição normal.[108] Existem vários testes de normalidade.
- O teste qui–quadrado de aderência para a distribuição normal permite testar se uma série de valores observados segue uma distribuição normal. Neste tipo de teste, a hipótese nula é que a distribuição observada pode ser aproximada pela distribuição normal. Tendo agrupado os valores observados, calcular as probabilidade de uma variável aleatória de distribuição normal pertencer a uma classe em estimativa dos parâmetros da distribuição devidos aos valores observados. Estas probabilidades podem ser obtidas com as tabelas numéricas da distribuição normal. Se a hipótese nula for verdadeira, a estatística qui–quadrado calculada a partir dos valores observados e das probabilidades anteriores seguem uma distribuição qui–quadrado. O número do grau de liberdade é se a média e o desvio padrão são conhecidos, se um dos dois parâmetros é desconhecido ou se os dois parâmetros são desconhecidos. A hipótese nula é rejeitada se a estatística qui–quadrado é superior ao valor obtido por meio da tabela do limiar da distribuição qui–quadrado .[124]
- O teste de Lilliefors é baseado na comparação entre a função de distribuição da distribuição normal e a função de distribuição empírica. É uma adaptação do teste de Kolmogorov–Smirnov. As opiniões sobre o poder do teste são divididas. Ele é eficiente em torno da média, mas nem tanto para a comparação das caudas de distribuição. Os valores observados são dispostos em ordem crescente . Os valores são as frequências teóricas da distribuição normal centrada reduzida associada com os valores normalizados. Se a estatística for superior a um valor crítico calculado pelo limiar e ao tamanho da amostra, então o pressuposto de normalidade é rejeitado no limiar .[125]
- O teste de Anderson–Darling é outra versão do teste de Kolmogorov–Smirnov mais adequada ao estudo das caudas de distribuição. Usando a mesma notação que o teste de Lilliefors, se a estatística for superior a uma valor crítico calculado pelo limiar e ao tamanho da amostra, então o pressuposto de normalidade é rejeitado no limiar .[125]
- O teste D'Agostino é baseado nos coeficientes de simetria e de curtose. É particularmente eficaz a partir de valores observados. Embora a ideia do teste seja simples, as fórmulas são mais complicadas. A ideia é construir modificações dos coeficientes de simetria e de curtose para obter as variáveis e da distribuição normal padrão. Então, é realizado um teste qui–quadrado com estatística .[125]
- O teste Jarque–Bera também é baseado nos coeficientes de simetria e de curtose. O teste somente é interessante para um número elevado de valores observados. Considerando os dois estimadores e , deve–se realizar um teste qui–quadrado com estatística .[125]
- O teste de Shapiro–Wilk proposto em 1965 é eficaz para pequenas amostras com menos de 50 valores. Os valore observados são dispostos em ordem crescente e os coeficientes são calculados a partir do quantil, da média, da variância e da covariância de uma distribuição normal. Se a estatística for inferior a um valor crítico calculado pelo limiar e ao tamanho da amostra, então o pressuposto de normalidade é rejeitado no limiar .[125]
Estimativa dos parâmetros
editarQuando um fenômeno aleatório é observado e considera–se que ele pode ser modelado por uma distribuição normal, uma das perguntas que podem ser feitas é quanto valem os parâmetros e da distribuição normal ? Então, é realizada uma estimativa. As observações coletadas durante a observação do fenômenos são notadas para as variáveis aleatórias . As notações da média aritmética e da média quadrada também são úteis: e .[126]
Estes dois valores são respectivamente estimadores da média e do desvio padrão que são calculados a partir dos valores observados. Como variáveis tem distribuição normal, então tem distribuição e tem distribuição qui–quadrado .[126]
Estimativa da média quando o desvio padrão é conhecido
editarUm método consiste em procurar um limiar de um intervalo de confiança em torno da média teórica . Usando os quantis de ordem e , a fórmula que define os quantis permite obter . Com os valores observados e as tabelas da distribuição normal padrão, então é possível fornecer os valores numéricos de intervalo de limiar .[126]
Estimativa da média quando o desvio padrão não é conhecido
editarUm método consiste em usar uma variável intermediária que pode ser escrita com as novas variáveis aleatórias de distribuição : tem distribuição de Student . Usando os quantis de ordem e , a fórmula que define os quantis permite obter . Com os valores observados e as tabelas da distribuição normal padrão, então é possível fornecer os valores numéricos de intervalo para limiar .[127]
Estimativa do desvio padrão quando a média é desconhecida
editarÉ o mesmo método que o anterior. A introdução da variável aleatória de distribuição qui–quadrado para grais de liberdade permite obter , em que e são quantis de distribuição qui–quadrado para grais de liberdade que poder obtido pela tabela do qui–quadrado. O intervalo é o intervalo de confiança para o limiar .[128]
Simulação
editarPara estudar um fenômeno aleatório que envolve uma variável normal, cujos parâmetros são conhecidos ou estimados, uma abordagem analítica muitas vezes é muito complexa para ser desenvolvida. Neste caso, é possível utilizar um método de simulação. Particularmente, o método de Monte Carlo que consiste em gerar uma amostra artificial de valores independentes de uma variável com um computador. Geralmente softwares ou linguagens de programação tem um gerador de números pseudoaleatórios com uma distribuição uniforme em . Então, transforma–se esta variável de distribuição em uma variável (adaptação de outros valores dos parâmetros não representa qualquer problema).[129]
Abordagens para evitar
editar- De maneira geral, pode–se utilizar a função inversa da função de distribuição: neste caso, a variável aleatória segue a distribuição normal padrão. Entretanto, este método não é conveniente por falta de expressões simples de funções e . Além disso, os resultados são numericamente insatisfatórios.[130]
- Se são doze variáveis independentes de distribuição uniforme em , então a variável tem média nula e desvio padrão unitário. Portanto, o devido ao teorema central do limite, esta variável segue aproximadamente a distribuição normal padrão. Esta é uma maneira simples de gerar uma distribuição normal, porém a aproximação permanece imprecisa.[131]
Abordagens eficientes
editar- Um melhor algoritmo é o método de Box–Muller, que utiliza uma representação polar de duas coordenadas uniformes dadas pelas fórmulas seguintes. Se , então , em que as duas variáveis resultantes são independentes. Este algoritmo é simples de ser realizado, mas o cálculo de um logaritmo, de uma raiz quadrada e de uma função trigonométrica retarda o processo.[131]
- Uma melhoria foi proposta por Marsaglia e Bray em 1964, que substitui os cosenos e os senos pelas variáveis e ou e independentes de distribuição e quando (são rejeitados os pares que não verificarem a última condição).[132] Portanto, Este algoritmo não é mais pesado para ser implementado e a simulação tem ganhado velocidade.[131]
- Para um grande número de impressões aleatórias, o método Ziggourat é mais rápido, mas a implementação é mais complexa.[133]
Implementação em software de computação
editarA distribuição normal foi incorporada em vários softwares de computação.
Planilhas
editarAs planilhas em Microsoft Excel, OpenOffice.org Calc e LibreOffice Calc fornecem as seguintes funções:[134][135][136]
LOI.NORMALE(x ; mu ; sigma ; cumulative)(em inglês,NORMDIST) : dá- se cumulative for booleano
FAUX, a densidade de probabilidade da distribuição normal de esperança mu e desvio padrão sigma em x. - se cumulative for booleano
VRAI, a função de distribuição da distribuição normal de esperança mu e desvio padrão sigma em x.
- se cumulative for booleano
PHI(x): dá a densidade de probabilidade da distribuição normal padrão φ em x.LOI.NORMALE.STANDARD(x)(NORMSDIST) : dá a função de distribuição da distribuição normal padrão Φ em x.LOI.NORMALE.INVERSE(p ; mu ; sigma)(NORMINV) dá o quantil q de uma distribuição normal para uma probabilidade p.LOI.NORMALE.STANDARD.INVERSE(p)(NORMSINV)CENTREE.REDUITE(x ; mu ; sigma)(STANDARDIZE) retorna (x – mu) / sigma.
Linguagem de programação estatística S
editarA linguagem S, implementada no software R e S–PLUS, fornece as seguintes funções:[137]
dnorm(): densidade de probabilidade da distribuição normaldnorm(x): para uma distribuição normal padrão em x ;dnorm(x, log=TRUE)dá o logaritmo natural do valor.dnorm(x, mu, sigma)oudnorm(x, mean = mu, sd = sigma): para uma distribuição normal de esperança mu e desvio padrão sigma em x ; pode ser adicionadolog = TRUE,
pnorm(): função de distribuição de uma distribuição normalpnorm(q): para uma distribuição normal padrão;lower.tail = FALSEdá o adicional 1 – Φ,log.p = TRUEdá o logaritmo natural do valorpnorm(q, mu, sigma)oupnorm(q, mean = mu, sd = sigma): idem para uma distribuição normal de esperança mu e desvio padrão sigma em x
qnorm(): dá os quantis de uma distribuição normalqnorm(p): para uma distribuição normal padrão;lower.tail = FALSEdá o quantil do adicional 1 – Φ,log.p = TRUEda o logaritmo natural do valorqnorm(p, mu, sigma)ouqnorm(p, mean = mu, sd = sigma): idem para uma distribuição normal de esperança mu e desvio padrão sigma
rnorm(): gerador de números aleatórios de acordo com uma distribuição normalrnorm(n): gerador de n números aleatórios em uma distribuição normal padrãornorm(n, mu, sigma)ournorm(n, mean = mu, sd = sigma): idem para uma distribuição normal de esperança mu e desvio padrão sigma
ks.test(A, "dnorm"): teste de normalidade de Kolmogorov–Smirnov
Matlab / Octave
editarO Matlab oferece os seguintes comandos:[138]
randn(n): gerador de n números aleatórios em uma distribuição normal padrão
randn(m, n): gerador de n números aleatórios em uma matriz mxnnormcdf(x, mu, sigma),cdf('norm', x, mu, sigma)ecdf('Normal', x, mu, sigma): função de distribuição em x da distribuição normal de esperança mu e desvio padrão sigma (função de distribuição cumulativa)normpdf(x, mu, sigma),pdf('norm', x, mu, sigma)epdf('Normal', x, mu, sigma): densidade de probabilidade em x da distribuição normal de esperança mu e desvio padrão sigma (função de distribuição de probabilidade)[mu, sigma] = normfit(X): determina a esperança e o desvio padrão de um conjunto de dados X de regressão
Scilab
editar- O Scilab (libre et gratuit) oferece os seguintes comandos:[139]
rand(m, n, "normal"): matriz mxn de números aleatórios de distribuição normal padrão;rand(A, "normal")dá uma matriz de mesma dimensão que a matriz Agrand(m, n, "nor", mu, sigma): matriz mxn de números aleatórios de distribuição normal de esperança mu e desvio padrão sigmacdfnor("PQ", x, mu, sigma): valor p da função de distribuição (função de distribuição cumulativa) em x para uma distribuição normal de esperança mu e desvio padrão sigmacdfnor("X", mu, sigma, p, 1 - p): valor do quantil q para uma probabilidade pcdfnor("Mean", sigma, p, 1 - p, x): esperança de uma distribuição normal com desvio padrão sigma e probabilidade cumulada em x para pcdfnor("Std", p, 1 - p, x, mu): desvio padrão de uma distribuição normal com probabilidade cumulada em x para p e esperança mu
- As opções
"Mean"e"Std"executam regressão se x e p são vetores. - A extensão Atoms CASCI fornecem outras funções que tem uma escrita mais simples.
cdfnormal(x): função de distribuição Φ da distribuição normal padrão
cdfnormal(x, mu, sigma): função de distribuição de uma distribuição normal de esperança mu e desvio padrão sigmaidfnormal(p): quantil Φ-1 da distribuição normal padrão (função de distribuição cumulativa inversa)
idfnormal(p, mu, sigma): idem para uma distribuição de esperança mu e desvio padrão sigmapdfnormal(x): densidade de probabilidade φ da distribuição normal padrão (função de distribuição de probabilidade)
pdfnormal(x, mu, sigma): idem para uma distribuição de esperança mu e desvio padrão sigmarndnormal(n): gerador de n números aleatórios em uma distribuição normal padrão;rndnormal(m, n)gera uma matriz mxnrndnormal(n, mu, sigma),rndnormal(m, n, mu, sigma): idem para uma distribuição de esperança mu e desvio padrão sigma
Homenagem
editarPor sua ampla utilização nas ciências, a distribuição normal, muitas vezes pela utilização da curva em forma de sino, é destacada em diferentes contextos e é utilizada para representar a universalidade da uma distribuição estatística, entre outros. Francis Galton menciona a distribuição normal em seu trabalho Natural Inheritance de 1889[10]:
| “ | Je ne connais rien d'autre si propre à frapper l'imagination que cette merveilleuse forme d'ordre cosmique donnée par la Loi de Fréquence des Erreurs... Elle règne avec sérénité et en toute abnégation au milieu de la confusion sauvage. | ” |
Em 1989, foi feita uma homenagem à Carl Friedrich Gauss com a impressão de um bilhete com seu rosto e a curva em forma de sino (pedras suportam a curva de sino, e o caso de alguns matemáticos).[140]
| O estatístico William Youden escreveu em 1962 uma explicação sobre a finalidade e a posição da distribuição normal nas ciências. Ele apresentou o caligrama em formato de sino.[141] |
THE |
| Em português, a lei normal do erro destaca-se na experiência da humanidade como uma das mais amplas generalizações de filosofia natural. Ela serve como instrumentos guias em pesquisas nas ciências físicas e sociais, na medicina, na agricultura e na engenharia. Ela é uma ferramenta essencial para a análise e a interpretação dos dados básicos obtidos pela observação e experimentação. |
Referências
- ↑ Bittencourt, Hélio Radke; Viali, Lori. «Contribuições para o Ensino da Distribuição Normal ou Curva de Gauss em Cursos de Graduação» (PDF). III Seminário Internacional de Pesquisa em Educação Matemática. Consultado em 10 de abril de 2017
- ↑ «3 – Processos Estocásticos» (PDF). Pontifícia Universidade Católica do Rio de Janeiro (PUC – Rio). Consultado em 10 de abril de 2017
- ↑ Davila, Victor Hugo Lachos. «Introdução às Séries Temporais» (PDF). Universidade Estadual de Campinas (UNICAMP). Consultado em 10 de abril de 2017
- ↑ Lestienne, Rémy (2008). O Acaso Criador. [S.l.]: edUSP. p. 61. 297 páginas
- ↑ «Distribuição Normal» (PDF). Universidade de São Paulo (USP). Consultado em 10 de abril de 2017
- ↑ «Teorema Central do Limite». Universidade Federal do Paraná (UFPR). Consultado em 10 de abril de 2017
- ↑ «Distribuição Normal – Estimação» (PDF). Universidade de São Paulo (USP). Consultado em 10 de abril de 2017. Arquivado do original (PDF) em 22 de agosto de 2017
- ↑ Duarte, Marcus Antonio Viana; Meola, Tatiana (Outubro de 2017). «Curso de Planejamento Experimental» (PDF). Universidade Federal de Uberlândia (UFU). Consultado em 10 de abril de 2017
- ↑ a b Bru, Bernard (2006). «La Courbe de Gauss ou le Théorème de Bernoulli Raconté aux Enfants» (PDF). Mathematics and Social Sciences. 175 (3): 5 – 23
- ↑ a b c d e f g h i j Fuchs, Aimé (1995). «Plaidoyer pour la Loi Normale» (PDF). Pour la Science: 17
- ↑ Stigler, Stephen (1999). Statistics on the Table. [S.l.]: Harvard University Press. p. 407. 499 páginas
- ↑ Stigler, Stephen (1999). Statistics on the Table. [S.l.]: Harvard University Press. p. 406. 499 páginas
- ↑ Lévy, Paul (1937). Théorie de L'Addition des Variables Aléatoires. [S.l.]: Gauthier – Villars. p. 42
- ↑ Lejeune, Michel (2006). Analyse Statistique des Données Spatiales. [S.l.]: Technip. p. 2
- ↑ A Guide to Tables of the Normal Probability Integral. National Institute of Standards and Technology: U.S. Government Publishing Office. 1952. p. 16
- ↑ a b Dodge, Yadolah (2004). Statistique – Dictionnaire Encyclopédique. [S.l.]: Springer–Verlag. p. 502. 637 páginas
- ↑ Larson, Ron; Farber, Betsy (2004). Estatística Aplicada. [S.l.]: Pearson Education do Brasil. 1 páginas
- ↑ a b c d e f Kahane, Jean–Pierre (1 de julho de 2009). «La Courbe en Cloche». CNRS – Images des Maths. Consultado em 16 de fevereiro de 2017
- ↑ Lifshits, M. A. (1995). Gaussian Random Functions. [S.l.]: Kluver Academic Publishers. p. 1. 339 páginas
- ↑ a b Larson, Ron; Farber, Betsy (2004). Estatística aplicada. [S.l.]: Pearson Education do Brasil. 1 páginas
- ↑ a b Dodge, Yadolah (2004). Statistique – Dictionnaire Encyclopédique. [S.l.]: Springer–Verlag. p. 309. 637 páginas
- ↑ Farias, Ana Maria Lima de; Kubrusly, Jessica Quintanilha; Souza, Mariana Albi de Oliveira. «GET00143 – Teoria das Probabilidades II – Variáveis Aleatórias Unidmensionais» (PDF). Universidade Federal Fluminense (UFF). p. 145. 222 páginas. Consultado em 10 de abril de 2017. Arquivado do original (PDF) em 11 de abril de 2017
- ↑ a b c d Lifshits, M. A. (1995). Gaussian Random Functions. [S.l.]: Kluver Academic Publishers. p. 2. 339 páginas
- ↑ Araujo, Maria Julieta Ventura Carvalho de. «Capítulo 3: Limite de uma Função e Continuidade» (PDF). Universidade Federal de Juiz de Fora. p. 52. Consultado em 17 de abril de 2017
- ↑ Tassi, Philippe; Legait, Sylvia (1990). Théorie des Probabilités en vue des Applications Statistiques. [S.l.]: Technip. p. 128. 367 páginas
- ↑ a b c d Cramér, Harald (1970). Random Variables and Probability Distributions. [S.l.]: Cambridge University Press. p. 50. 123 páginas
- ↑ a b Grinstead, Charles Miller; Snell, James Laurie (1997). Introduction to Probability 2ª ed. [S.l.]: American Mathematical Society. p. 330. 519 páginas
- ↑ a b Marsaglia, George (2004). «Evaluating the Normal Distribution». Journal of Statistical Software. 11 (4): 1 – 11
- ↑ Geller, Daryl N. «Lebesgue-Stieltjes Integrals» (PDF). Stony Brook University. pp. 1 – 4. Consultado em 17 de abril de 2017
- ↑ a b c Ministère de l'Éducation Nationale de la Jeunesse et de la Vie Associative (2012). «Ressources pour la Classe Terminale Générale et Technologique – Probabilités et Statistique» (PDF)
- ↑ Droesbeke, Jean-Jacques; Lejeune, Michel; Saporta, Gilbert (2005). Modèles Statistiques pour Données Qualitatives. [S.l.]: Technip. p. 104. 295 páginas
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 122. 387 páginas
- ↑ a b c Cramér, Harald (1970). Random Variables and Probability Distributions 3ª ed. [S.l.]: Cambridge University Press. p. 51. 123 páginas
- ↑ Paula, Fábio P. Machado e Gilberto A. (2016). «Teorema do Limite Central» (PDF). IMEUSP. p. 38. Consultado em 17 de abril de 2017
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 123. 387 páginas
- ↑ a b Protassov, Konstantin (2002). Analyse Statistique des Données Expérimentales. [S.l.]: EDP Sciences. p. 27. 148 páginas
- ↑ a b c d Protassov, Konstantin (2002). Analyse Statistique des Données Expérimentales. [S.l.]: EDP Sciences. p. 28. 148 páginas
- ↑ Bussab, Wilton de O.; Pedro A., Morettin (2010). Estatística básica. São Paulo: Saraiva. 176 páginas
- ↑ Ross, Sheldon M. (2007). Initiation aux Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. p. 408. 592 páginas
- ↑ Dodge, Yadolah (2004). Statistique – Dictionnaire Encyclopédique. [S.l.]: Springer–Verlag. p. 310. 637 páginas
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 116. 387 páginas
- ↑ a b Ross, Sheldon M. (2007). Initiation aux Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. p. 239. 592 páginas
- ↑ Viali, Lorí. «Série probabilidade» (PDF). PUCRS. p. 2. Consultado em 17 de abril de 2017
- ↑ a b c d Weisstein, Eric W. «Gaussian Function». MathWorld. Consultado em 22 de fevereiro de 2017
- ↑ Droesbeke, Jean–Jacques; Lejeune, Michel; Saporta, Gilbert (2005). Modèles Statistiques pour Données Qualitatives. [S.l.]: Technip. p. 85
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 120. 387 páginas
- ↑ Protassov, 2002, p. 28.
- ↑ SAMPAIO, JOAO CARLOS VIEIRA. «Integração por partes» (PDF). UFSCAR. p. 141. Consultado em 17 de abril de 2017
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 119
- ↑ «6 – Medidas de Assimetria e Curtose» (PDF). Universidade de São Paulo (USP). Consultado em 10 de abril de 2017
- ↑ Casella, George; Berger, Roger L. (2010). Inferência Estatística. [S.l.]: Centage Learning. p. 72
- ↑ Abramowitz, Milton; Stegun, Irene (1972). Handbook of Mathematical Functions with Formulas 9ª ed. New York: Dover. p. 930
- ↑ Grinstead, Charles Miller; Snell, James Laurie (1997). Introduction to Probability 2ª ed. [S.l.]: American Mathematical Society. p. 345. 519 páginas
- ↑ Protassov, Konstantin (2002). Analyse Statistique des Données Expérimentales. [S.l.]: EDP Sciences. p. 44. 148 páginas
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica. São Paulo: Saraiva. 143 páginas
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica. São Paulo: Saraiva. 77 páginas
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 223. 387 páginas
- ↑ Yger, Alain; Weil, Jacques–Arthur (2009). Mathématiques Appliquées. [S.l.]: Pearson Education. p. 651. 890 páginas
- ↑ Waiandt, Euclésio Rangel (2014). «Alguns Teoremas Limites para Sequência de Variáveis Aleatórias» (PDF). Universidade Federal do Espírito Santo. p. 11. Consultado em 17 de abril de 2017
- ↑ Araujo, Tarciana Liberal Pereira de. «Probabilidade II» (PDF). Universidade Federal da Paraíba. p. 2. Consultado em 17 de abril de 2017
- ↑ Araujo, Tarciana Liberal Pereira de. «Probabilidade II» (PDF). Universidade Federal da Paraíba. p. 3. Consultado em 17 de abril de 2017
- ↑ Araujo, Tarciana Liberal Pereira de. «Probabilidade II» (PDF). Universidade Federal da Paraíba. p. 5. Consultado em 17 de abril de 2017
- ↑ Ross, Sheldon M. (2007). Initiation aux Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. p. 299. 592 páginas
- ↑ a b c Gomes, Luís Aguiar. «Convolução e Transformadas de Fourier» (PDF). Faculdade de Ciências Exatas e da Engenharia. pp. 8 – 10. Consultado em 17 de abril de 2017
- ↑ Lifshits, M. A. (1995). Gaussian Random Functions. [S.l.]: Kluver Academic Publishers. p. 4. 339 páginas
- ↑ Cramér, Harald (1970). Random Variables and Probability Distributions 3ª ed. [S.l.]: Cambridge University Press. p. 52. 123 páginas
- ↑ Cramér, Harald (1970). Random Variables and Probability Distributions 3ª ed. [S.l.]: Cambridge University Press. p. 53. 123 páginas
- ↑ Ross, Sheldon M. (2007). Initiation aux Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. p. 235. 592 páginas
- ↑ Mandelbrot, Benoît (1966). «Nouveaux Modèles de la Variation des Prix (Cycles Lents et Changements Instantanés)». Cahiers du Séminaire d'Économétrie (9): 53 – 66
- ↑ «Distribuição de probabilidade» (PDF). PUC-RIO. p. 6. Consultado em 19 de abril de 2017
- ↑ McCulloch, J. Huston (1 de janeiro de 1986). «Simple consistent estimators of stable distribution parameters». Communications in Statistics - Simulation and Computation. 15 (4): 1109–1136. ISSN 0361-0918. doi:10.1080/03610918608812563
- ↑ Lifshits, M. A. (1995). Gaussian Random Functions. [S.l.]: Kluver Academic Publishers. p. 125. 339 páginas
- ↑ IVANISVILI, AATA (16 de maio de 2016). «BOUNDARY VALUE PROBLEM AND THE EHRHARD INEQUALITY» (PDF). Cornell University Library. p. 16. Consultado em 19 de abril de 2017
- ↑ Shannon, Claude (1948). «A Mathematical Theory of Communication» (PDF). The Bell System Technical Journal. 27: 379 – 423
- ↑ Allison, Lloyd (2012). «Normal, Gaussian». Consultado em 2 de março de 2017
- ↑ a b Abramowitz, Milton; Stegun, Irene (1972). Handbook of Mathematical Functions with Formulas 9ª ed. New York: Dover. p. 932. 1047 páginas
- ↑ a b Tassi, Philippe; Legait, Sylvia (1990). Théorie des Probabilités en vue des Applications Statistiques. [S.l.]: Technip. p. 126. 367 páginas
- ↑ Bonini, Edmundo Eboli (1979). «Principais tabelas estatísticas aplicadas à contabilidade e à auditoria». Principais tabelas estatísticas aplicadas à contabilidade e à auditoria. p. 1. Consultado em 19 de abril de 2017
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 354. 387 páginas
- ↑ a b Grinstead, Charles Miller; Snell, James Laurie (1997). Introduction to Probability 2ª ed. [S.l.]: American Mathematical Society. p. 213. 519 páginas
- ↑ Grinstead, Charles Miller; Snell, James Laurie (1997). Introduction to Probability 2ª ed. [S.l.]: American Mathematical Society. p. 214. 519 páginas
- ↑ «Tabelas Esatatística» (PDF). Universidade do Minho. 2008. p. 26. Consultado em 19 de abril de 2017
- ↑ Protassov, 2002, p. 72.
- ↑ Protassov, Konstantin (2002). Analyse Statistique des Données Expérimentales. [S.l.]: EDP Sciences. p. 44. 72 páginas
- ↑ a b c d Protassov, Konstantin (2002). Analyse Statistique des Données Expérimentales. [S.l.]: EDP Sciences. p. 29. 148 páginas
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 90. 387 páginas
- ↑ «Capítulo X – Teste do Qui-quadrado, χ2» (PDF). Universidade de Coimbra. 2007. pp. 89 – 166. Consultado em 19 de abril de 2017
- ↑ Viali, Lorí (2008). «Teste de hipótese não paramétrico» (PDF). UFRGS. p. 8. Consultado em 19 de abril de 2017
- ↑ Costa, Antônio Fernando Branco; Magalhães, Maysa Sacramento de (18 de maio de 2005). «O uso da estatística de qui-quadrado no controle de processos» (PDF). The Scientific Electronic Library Online. 2 páginas. Consultado em 19 de abril de 2017
- ↑ Ross, Sheldon M. (2007). Initiation aux Probabilités. [S.l.]: Presses Polytechniques et Universitaires Romandes. p. 301. 592 páginas
- ↑ Yger, Alain; Weil, Jacques–Arthur (2009). Mathématiques Appliquées. [S.l.]: Pearson Education. p. 703. 890 páginas
- ↑ Yger y Weil, 2009, p. 703.
- ↑ a b Ferrari, Nicolas (2006). «Prévoir l'investissement des Entreprises – Un Indicateur des Révisions dans l'Enquête Investissement». Économie et Statistique (395 – 396): 39 – 64
- ↑ Bogaert, 2006, p. 330.
- ↑ a b Pham–Gia, T.; Turkkan, N.; Marchand, E. (1º de setembro de 2006). «Density of the Ratio of Two Normal Random Variables and Applications». Communications in Statistics – Theory and Methods. 35: 1569 – 1591
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 341. 387 páginas
- ↑ Duque, Oscar Mario Londoño (12 de dezembro de 2014). «Uma breve análise do movimento Browniano» (PDF). Universidade Federal do Espírito Santo. p. 68. Consultado em 19 de abril de 2017
- ↑ Henze, Norbert (1986). «A Probabilistic Representation of the 'Skew–Normal' Distribution». Scandinavian Journal of Statistics. 13 (4): 271 – 275
- ↑ Santos, Caroline Oliveira; Scalon, João Domingos; Ozaki, Vitor Augusto (2014). «A distribuição normal-assimétrica como modelo para produtividade de milho aplicada ao seguro agrícola1». The Scientific Electronic Library Online. p. 1. Consultado em 19 de abril de 2017
- ↑ Rouzet, G. (1962). «Étude des Moments de la Loi Normale Tronquée». Revue de Statistique Appliquée. 10 (2): 49 – 61
- ↑ Hochreiter, Sepp; Clevert, Djork–Arne; Obermayer, Klaus (2006). «A New Summarization Method for Affymetrix Probe Level Data» (PDF). Bioinformatics. 22 (8): 943 – 949
- ↑ Irvine, Richard (2002). «A Geometrical Approach to Conflict Probability Estimation» (PDF). Air Traffic Control Quarterly Seminar. 10 (2): 1 – 15
- ↑ Hosking, J. R. M.; Wallis, James R. (1997). Regional Frequency Analysis: An Approach Based on L–Moments. [S.l.]: Cambridge University Press. p. 197. 224 páginas
- ↑ «Variáveis aleatórias contínuas: distribuições e aplicações» (PDF). Companhia de Pesquisa de Recursos Minerais - Serviço Geológico do Brasil. p. 141. Consultado em 19 de abril de 2017
- ↑ a b Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 86. 387 páginas
- ↑ Zuben, Fernando J. Von; Attux, Romis R. F. (2010). «Polinômios de Hermite e Splines» (PDF). Universidade de Campinas. pp. 20 – 22. Consultado em 19 de abril de 2017
- ↑ Pasquali, Luiz. «A curva normal» (PDF). Universidade de Brasília. pp. 1 – 8. Consultado em 19 de abril de 2017. Arquivado do original (PDF) em 19 de novembro de 2008
- ↑ a b c Seddik-Ameur, Nacira (2003). «Les Tests de Normalité de Lhoste». Mathematics and Social Sciences. 41 (162): 19 – 43
- ↑ Bogaert, Patrick (2006). Probabilités pour Scientifiques et Ingénieurs. Paris: Éditions De Boeck. p. 68. 387 páginas
- ↑ Mollo, Suzanne (1975). «Tort (Michel). — Le Quotient Intellectuel». Revue Française de Pédagogie. 33 (33): 66 – 68
- ↑ Ridley, Mark (2004). Evolution 3ª ed. [S.l.]: Blakwell. p. 76. 751 páginas
- ↑ a b Ridley, Mark (2004). Evolution 3ª ed. [S.l.]: Blakwell. p. 226. 751 páginas
- ↑ Ridley, Mark (2004). Evolution 3ª ed. [S.l.]: Blakwell. p. 252. 751 páginas
- ↑ Borghi, de Onis; Garza, Van den Broeck; Frongillo, Grummer–Strawn, Van Buuren, Pan; Molinari, Martorell; Onyango, Martines (2006). «Construction of the World Health Organization Child Growth Standards: Selection of Methods for Attained Growth Curves» (PDF). Statistics in Medecine. 25: 247 – 265
- ↑ Hosking, J. R. M.; Wallis, James R. (1997). Regional Frequency Analysis: An Approach Based on L–Moments. [S.l.]: Cambridge University Press. p. 157. 224 páginas
- ↑ Dodge, Yadolah (2004). Statistique – Dictionnaire Encyclopédique. [S.l.]: Springer–Verlag. p. 354. 637 páginas
- ↑ a b c Mandelbrot, Benoît (1966). «Nouveaux Modèles de la Variation des Prix (Cycles Lents et Changements Instantanés)». Cahiers du Séminaire d'Économétrie (9): 53 – 66
- ↑ Yger, Alain; Weil, Jacques–Arthur (2009). Mathématiques Appliquées. [S.l.]: Pearson Education. p. 573. 890 páginas
- ↑ Filho, Herondino (2014). «Distribuição Normal» (PDF). UNIFAP. p. 2. Consultado em 19 de abril de 2017
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica. São Paulo: Saraiva. 311 páginas
- ↑ Tassi, Philippe; Legait, Sylvia (1990). Théorie des Probabilités en vue des Applications Statistiques. [S.l.]: Technip. p. 144. 367 páginas
- ↑ Dodge, Yadolah (2004). Statistique – Dictionnaire Encyclopédique. [S.l.]: Springer–Verlag. p. 228. 637 páginas
- ↑ Ghasemi, Asghar; Zahediasl, Saleh (1 de janeiro de 2012). «Normality Tests for Statistical Analysis: A Guide for Non-Statisticians». International Journal of Endocrinology and Metabolism. 10 (2): 486–489. ISSN 1726-913X. PMID 23843808. doi:10.5812/ijem.3505
- ↑ Dodge, Yadolah (2004). Statistique – Dictionnaire Encyclopédique. [S.l.]: Springer–Verlag. p. 519. 637 páginas
- ↑ a b c d e Rakotomalala, Ricco (2011). «Tests de Normalité» (PDF). Université Lumière Lyon 2. Consultado em 2 de março de 2017
- ↑ a b c Yger, Alain; Weil, Jacques–Arthur (2009). Mathématiques Appliquées. [S.l.]: Pearson Education. p. 715. 890 páginas
- ↑ Yger, Alain; Weil, Jacques–Arthur (2009). Mathématiques Appliquées. [S.l.]: Pearson Education. p. 716. 890 páginas
- ↑ Yger, Alain; Weil, Jacques–Arthur (2009). Mathématiques Appliquées. [S.l.]: Pearson Education. p. 717. 890 páginas
- ↑ Muller, Ademir (2008). «SIMULAÇÃO ESTOCÁSTICA: O MÉTODO DE MONTE CARLO» (PDF). UFPR. p. 11. Consultado em 19 de abril de 2017
- ↑ Chhikara, Raj S.; Folks, J. Leroy (1989). The Inverse Gaussian distribution. New York: Marcel Dekker. 8 páginas
- ↑ a b c Atkinson, A. C.; Pearce, M. C. (1976). «The Computer Generation of Beta, Gamma and Normal Random Variables». Journal of the Royal Statistical Society. 139 (4): 431 – 461
- ↑ Marsaglia, George; Bray, Thomas A. (1964). «A Convenient Method for Generating Normal Variables». SIAM Review. 6 (3): 260 – 264
- ↑ Marsaglia, George; Tsang, Wai Wan. «The Ziggurat Method for Generating Random Variables» (PDF). CORE. p. 2. Consultado em 20 de abril de 2017
- ↑ «Normal Distribution Probability in Excel». Statistics How To (em inglês)
- ↑ «Documentation/How Tos/Calc: NORMSDIST function - Apache OpenOffice Wiki». wiki.openoffice.org. Consultado em 23 de abril de 2017
- ↑ «Funções estatísticas - Parte 4 - LibreOffice Help». help.libreoffice.org. Consultado em 23 de abril de 2017
- ↑ Krause, Andreas; Olson, Melvin (14 de março de 2013). The Basics of S and S-PLUS (em inglês). [S.l.]: Springer Science & Business Media. p. 114. ISBN 9781475727517
- ↑ «Normal Distribution - MATLAB & Simulink». www.mathworks.com. Consultado em 23 de abril de 2017
- ↑ «cdfnor - Cumulative distribution function normal distribution». help.scilab.org (em inglês). Consultado em 23 de abril de 2017
- ↑ Michon, Gerard. «Coat-of-arms of Carl Friedrich Gauss (1777-1855) - Numericana». www.numericana.com (em inglês). Consultado em 23 de abril de 2017
- ↑ Stigler, Stephen (1999). Statistics on the Table. [S.l.]: Harvard University Press. p. 415. 499 páginas

















