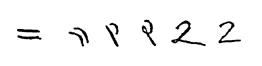2 (liczba)

2

0 1 2 3 4 5 6 7 8 9 10 0 10 20 30 40 50 60 70 80 90 100
faktoryzacja	liczba pierwsza
dzielniki	1, 2
zapis rzymski	II
dwójkowo	10
ósemkowo	2
szesnastkowo	2
przedrostki	di- (gr.) dou- (łac.)
Wartości funkcji arytmetycznych
φ(2) = 1 τ(2) = 2 σ(2) = 3 π(2) = 1 μ(2) = -1 M(2) = 0

2 (dwa) – liczba naturalna następująca po 1 i poprzedzająca 3. 2 jest też cyfrą wykorzystywaną do zapisu liczb w różnych systemach liczbowych, np. w ósemkowym, dziesiętnym i szesnastkowym. Warunkiem podzielności przez 2 liczby zapisanej w systemach liczbowych o podstawie parzystej (w tym w dziesiętnym) jest parzystość ostatniej cyfry. Jest to jedyna parzysta liczba pierwsza.

Historia

Symbol dwa używany współcześnie wywodzi się od hinduskich Braminów, którzy zapisywali dwójkę jako dwa poziome odcinki (taki kształt tego symbolu został przyjęty w Chinach i do dziś jest tam używany; łatwo też zauważyć analogię do rzymskiego symbolu II). W hinduskim państwie Gupta odcinki odwrócono o 45 stopni, czasami również górny odcinek skracano i zaginano ku środkowi dolnego odcinka. W Nagari, dla przyspieszenia zapisu, górny odcinek zaczęto łączyć z dolnym. Współczesny kształt otrzymujemy przywracając dolny odcinek do pozycji poziomej, ale górny pozostawiając jako krzywą łączącą się z odcinkiem dolnym.

Dwa w matematyce

• Warunek podzielności zapisanej w systemie dziesiętnym liczby przez 2, to aby miała ona ostatnią cyfrę 0, 2, 4, 6 lub 8
• Liczbę całkowitą podzielną przez 2 nazywamy liczbą parzystą
• 2 jest najmniejszą liczbą pierwszą
• 2 jest jedyną parzystą liczbą pierwszą

Dwa w nauce

• liczba atomowa helu
• obiekt na niebie Messier 2
• galaktyka NGC 2
• planetoida (2) Pallas

Dwa w kalendarzu

2. dniem w roku jest 2 stycznia. Zobacz też co wydarzyło się w 2 roku n.e.

2. miesiącem w roku jest luty.

Zobacz też

• dwójkowy system liczbowy
• dzielnik i cechy podzielności
• symbolika liczb