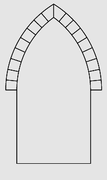
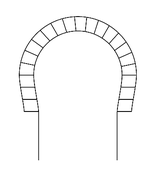
Arc (architecture)

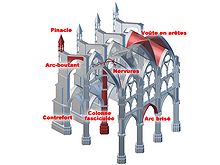





L’arc est l'élément d'ossature de directrice courbe ou polygonale, qui enjambe l'espace ouvert entre deux piliers (pieds-droits, etc.) ou murs en transmettant toute la charge qu'il supporte aux appuis (culées, contreforts, etc.), moyennant une force oblique dénommée « poussée[1] ».
En architecture s'est toujours présenté le problème de combler l'espace entre deux appuis. Avant l'invention du béton armé et des poutrelles en acier, la façon la plus simple de faire était d'utiliser une seule pièce de linteau, ou de poutre qui pouvait être en bois ou en pierre, et lorsqu'il n'y avait pas les pièces de la taille requise, diverses pièces plus petites, travaillées de sorte qu'elles puissent résister aux sollicitations mécaniques en jeu.
Fonctionnellement, une arche est réalisée dans la longueur d'un mur comme couronnement d'une ouverture (une baie, son embrasure) ou d'une travée. Traditionnellement, un arc est composé de claveaux (en pierre de taille, brique, adobe) qui travaillent toujours en compression et qui peuvent adopter des formes et courbes diverses. Cet ensemble constructif permet donc d'enjamber des espaces relativement importants via l'appareillage de pièces de dimensions réduites.
Quoiqu'assez simple, et d'usage commun dans la construction de structures depuis des temps reculés, le fonctionnement des arcs n'a été étudié scientifiquement qu'à partir du premier tiers du XIXe siècle. Avant cela, la conception des arches et des voûtes, mais aussi les dômes, faisait rentrer en jeu des méthodes empiriques géométriques qui permettaient de déterminer l'épaisseur à donner aux membres, ou la résistance et la forme à donner aux culées. Ces méthodes constructives manquaient de fondement scientifique et se basaient sur la capacité surdimensionnée des structures, généralement des appuis ou l'usage de tirants[2]. L'émergence de nouvelles disciplines d'étude à partir du XIXe siècle a largement permis de théoriser l'arc, son travail, et les causes de son effondrement. L'emploi de nouveaux matériaux constructifs, au début du XXe siècle, comme le fer forgé, l'acier et le béton armé a permis également la construction d'arcs continus de grande taille, déplaçant aussi le domaine de sa construction dans le champ d'expertise de l'ingénierie plus que celui de la maçonnerie ou de l'architecture.
Caractéristiques
[modifier | modifier le code]Structurellement, une arche avec voussoirs fonctionne comme un ensemble d'éléments qui transmettent les charges propres ou provenant d'autres éléments, aux murs ou aux piliers qui les supportent. De cette façon, l'arc est un système en équilibre. Du fait de leur propre morphologie, les segments sont soumis fondamentalement à des efforts de compression, mais ils transmettent des poussées horizontales aux points d'appui, vers l'extérieur, d'une manière qui tend à provoquer leur séparation. Pour contrecarrer ces actions, d'autres arcs sont généralement attachés, pour les équilibrer, des murs de masse suffisante aux extrémités, ou un système de contreventement constitué d'arcs-boutants ou de contreforts (donnant naissance aux arcs brisés et aux voûtes nervurées). Parfois, des tirants métalliques sont utilisés, ou parfois en bois, pour maintenir les segments inférieurs.
Un arc du point de vue de l'analyse structurelle est en définitive une structure hyperstatique (ou « statiquement indéterminée ») du troisième degré. Pour cette raison, trois articulations feraient d'un arc une structure déterminée statiquement (isostatique). Cette idée permet de connaître la valeur de la charge de rupture, ou d'effondrement d'un arc[3].
À partir de la structure d'un arc, d'autres éléments constructifs communs à l'architecture sont déduits tels que les voûtes et les dômes. Une voûte est générée en superposant des arcs égaux, correctement agencés, pour obtenir finalement un élément constructif « de surface » ; si les arcs sont en plein cintre, la surface sera semi-cylindrique. Un dôme peut être construit par la conjonction d'arcs égaux qui reposent sur une circonférence ; si les arcs sont en plein cintre, la surface sera hémisphérique.
Fabrication
[modifier | modifier le code]En règle générale, sont utilisés des matériaux qui résistent bien à la compression et peu à la traction, tels que pierre de taille, brique de terre cuite ou de terre crue. La façon la plus naturelle de ménager de grandes baies est l'utilisation d'arches[4]. Si la forme de l'arc est correcte, tous les claveaux travaillent en compression.
Dans les arches en pierre, les claveaux ont la forme d'un solide appelé « coin tronqué ». Ces voussoirs font souvent partie de l'appareil du mur. Certains auteurs feront école et écriront sur la construction des arches. L'architecte italien Leon Battista Alberti a conseillé que les claveaux soient grands et très semblables les uns aux autres. La clé d'arc doit être la pierre la plus lourde de toutes, les joints entre claveaux forment un plan perpendiculaire à la ligne courbe de l'intrados. Les pierres ont généralement une très grande résistance à la compression, en plus d'une faible compressibilité. C'est pour cette raison que la pierre a été utilisée depuis l'Antiquité comme matériau commun dans la construction des arches. Ces claveaux en pierre ont été bloqués dans certains cas avec un mortier qui assure une adhérence supplémentaire entre les éléments constructifs. La résistance à la compression des briques est, en règle générale, inférieure à celle des pierres.
Théorie de l'arc
[modifier | modifier le code]Dans un arc, les forces de compression verticales (poids propre et surcharges) sont transmises sous forme de forces latérales. Pour cette raison, les arcs doivent être construits à côté d'éléments qui font office de butée, tel qu'un mur de soutènement. Les voussoirs de l'arc, par leur forme, transmettent les forces verticales, les convertissant en deux composantes : une horizontale et une verticale. Calculer la poussée d'une arche, et pouvoir décider quelle dimension la culée doit avoir, de sorte que l'arc est stable, est un problème constructif des plus fondamentaux. Certains l'ont défini comme l'« énigme de l'architecture[5] ».
Toutes les structures incurvées ne sont pas une arche : un bossoir, un porte-à-faux incurvé ou une simple poutre cintrée encastrée en porte-à-faux (corbeau) sont toutes de fausses arcades (encorbellement). Toutes étant des structures courbes ou polygonales ne transmettent pas de poussée horizontale et sont plutôt considérées comme des structures isostatiques.
La définition d'une ligne de poussée à l'intérieur de la structure de l'arc a été depuis le milieu du XIXe siècle la théorie la plus répandue dans les traités de construction. Cependant, étant donné la lourdeur de cette procédure mathématique, le calcul de la ligne de poussée était généralement effectué à l'aide de méthodes graphiques ou, au moyen de maquettes réalisées à petite échelle. Actuellement, la méthode dite de l'état limite est appliquée à la détermination des éléments d'un arc.
Construction
[modifier | modifier le code]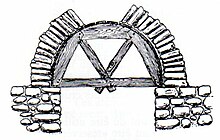
Depuis l'Antiquité, les arcs ont été élaborés à l'aide de cintres : une structure auxiliaire en bois qui offre un support initial aux voussoirs avant le placement de la clé. Ledit support a une forme de treillis et sa mission est de supporter le poids des éléments de l'arc jusqu'à ce que la clé d'arc soit ajustée. Le placement du segment central qui ferme l'arc (dénommé « clef ») génère l'engagement solidaire des voussoirs. En règle générale, ce dernier élément de l'arche est placé entre les contre-voussoirs de l'arche avec un marteau (généralement un marteau en bois) fermant complètement la structure.
Une fois cette dernière pierre installée, la structure auxiliaire en bois est démontée. À partir de cet instant l'arche, libérée de son cintre, entre en charge. Les cintres, réalisés en bois rendent en règle générale la construction d'arches assez coûteuse. Une grande partie de l'étude des arcs consistait à les faire avec des formes simples. Lorsque les formes en bois sont enlevées, les voussoirs commencent à entrer en compression l'un contre l'autre. C'est pour cette raison que le décoffrage doit être réalisé avec un soin extrême, et dans un ordre précis. De cette manière, l'arc n'a pas été soumis à des contraintes ajoutées ou décentrées. Il y a des exemples dans la littérature de l'effondrement des arcs dans le processus de décoffrage.
Effondrement et fissures
[modifier | modifier le code]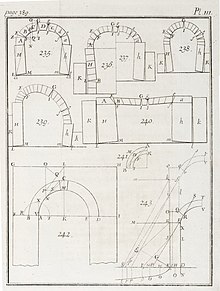
Une arche s'effondre lorsque les voussoirs qui la tiennent basculent d'un système statique, à un système dynamique en mouvement. L'ingénieur français Philippe de La Hire est le premier à analyser comment se fissure un arc. Le processus de décoffrage engendre nécessairement des fissures dans la structure d'une arche, du fait de la descente de la clé et au tassement des parties de l'arche. La maçonnerie a tendance à « descendre » après désengagement, cette opération provoque l'apparition de fissures à l'intérieur de la clé et dans les tiers de l'extrados (reins). Ces fissures d'adaptation des voussoirs sont très naturelles et donnent lieu à une situation d'équilibre différente de celle initialement calculée. En règle générale, l'effondrement de la structure résulte d'un calcul inadéquat des culées devant supporter l'arc qui, du fait de sa faiblesse, finit par produire son désengagement.
Dans l'analyse plastique des structures en arc de cercle, pour l'analyse des affaissement, trois hypothèses de base sont considérées[6]. Tout d'abord, on suppose que la résistance à la compression est infinie, ce qui signifie que l'on suppose que le matériau de l'arc est véritablement capable de supporter n'importe quelle charge sans s'effondrer. Au contraire, la deuxième hypothèse considère que le matériau possède une résistance à la traction nulle. Et troisièmement, que l'effondrement dû au glissement des segments est impossible, ce qui signifie que la résistance ou adhésion entre éléments est suffisante pour maintenir la structure de l'arc dans sa forme initiale. De ces trois hypothèses on a formulé une série de principes sur la stabilité et l'effondrement des arcs[7]. Le premier est libellé comme suit : « L'effondrement d'un arc chargé ne se produira pas si, dans chaque état de charge successif qui traverse la structure, il est possible de trouver un état d'équilibre statiquement admissible. »
Dans la théorie de l'effondrement des arcs, on peut dire qu'un arc est sûr lorsqu'il contient une ligne de poussée statiquement admissible. L'expression « statiquement admissible » vient indiquer que la structure de charge est conforme aux lois de la statique. Ce principe découle de l'observation d'arcs fissurés qui ont duré des siècles avec une configuration d'équilibre différente de celle initialement prévue. Dans la même ligne, il existe un second principe de l'effondrement d'une arche : « L'effondrement d'un arc se produira si une “configuration d'effondrement” cinématique peut être trouvée. »
Une configuration d'effondrement est une structure dans laquelle un certain nombre de rotules (ou articulations) se produisent. C'est-à-dire qu'un arc s'effondre quand il y a tellement de fissures qu'il finit par devenir un système mécanique (cinématique ou avec mouvement). L'apparition de fissures fait que l'arc est dans un équilibre instable. Ce principe a fait que l'apparition de fissures a été étudiée en détail, ainsi que sa relation avec le principe des puissances virtuelles.
Histoire
[modifier | modifier le code]L'arc occupe six mille ans de l'histoire de la construction[8]. Il apparaît pour la première fois dans l'architecture de la Mésopotamie et il se transmet à l'Europe, moyennant son emploi par l'Empire romain, jusqu'à atteindre son apogée au XVIe siècle[9]. Cet aboutissement est redevable à l'intuition des constructeurs médiévaux qui, sans connaître la théorie de l'arc, construisirent des cathédrales et des ponts qui restent encore debout aujourd'hui[10]. On peut dire que l'histoire des arcs passe par trois étapes, une première dans laquelle les arcs sont élaborés suivant l'intuition et l'expérience des constructeurs, une autre dans laquelle les propriétés empiriques sont obtenues dans des modèles géométriques (certains sans inspiration scientifique) et une troisième dans laquelle des modèles analytiques modernes nous permettent de savoir comment fonctionne « un arc ».
Période intuitive
[modifier | modifier le code]Dans la nature, il apparaît des arches naturelles, soit celles qui se forment spontanément dans les cols de montagne, en raison de l'effondrement des pierres, ordonnées dans l'arrangement isostatique stable d'une arche. Dans les grottes, par l'érosion de divers agents (tels que le vent et l'eau), elles forment des passages et espaces en forme d'arc. Tous ces arcs spontanés, formés dans la nature, ont peut-être inspiré les premiers hommes qui ont agencé des pierres en reproduisant à l'identique cette disposition courbe. Les arches avaient des significations magiques en raison de leur capacité à tenir « par elles-mêmes » et, dans certaines cultures, les grandes arches des ponts ont été attribuées à l'œuvre du diable[11]. L'usage habituel des arches dans les bâtiments, dans certaines cultures, ouvrait le chemin vers une connaissance empirique qui se développerait plus tard en lois géométriques. Beaucoup de traités de l'Antiquité montrent cette connaissance de la construction d'arcs à travers l'utilisation de dessins géométriques.
Développement empirique
[modifier | modifier le code]
L'arc est apparu en Mésopotamie et dans la civilisation de la vallée de l'Indus. Il a été en usage dans l'Égypte antique, en Assyrie, en Étrurie et plus tard dans la Rome antique. L'arc était utilisé dans les bâtiments auxiliaires, les structures souterraines et le drainage ; les Romains ont été les premiers à les utiliser dans des constructions monumentales, bien que l'on ait cru que les architectes romains apprirent leur utilisation des Étrusques. Le soi-disant arc romain est semi-circulaire et construit à partir d'un nombre impair de claveaux, de sorte qu'il existe une clé de voûte centrale. Les Romains utilisaient ce type d'arche semi-circulaire dans beaucoup de structures traditionnelles, telles qu'aqueducs, palais et amphithéâtres. Cet arc en plein cintre romain a été considéré par les architectes jusqu'au XVIIIe siècle comme la plus stable des arches[12]. Un exemple de construction empirique était la populaire « règle du tiers » qui, dans les arcs en plein cintre, était suffisante pour dimensionner une culée avec l'épaisseur de la troisième partie de son creux.
Au Moyen Âge, l'utilisation d'arcades avec voussoirs de pierre a atteint un développement technique important dans la construction des cathédrales ; il est encore utilisé aujourd'hui dans certaines structures comme les ponts[13] mais avec des matériaux variés. Au XIIe siècle, l'architecture gothique a commencé à utiliser l'arc brisé qui apprend des expériences antérieures : dans les structures romanes, les arcs semi-circulaires ne sont pas parfaits, puisque certains se sont dégradés par les reins (milieu de chaque semi-arc), et l'on a cherché à établir une arche dans laquelle les reins étaient moins en saillie, d'où l'arc brisé. Les règles de construction des arcs se retrouvent dans la tradition verbale des corporations de maçons médiévales. Dans de nombreux cas, ces règles étaient complexes à comprendre et peu de ces règles nous sont parvenues directement par des écrits[14]. Dans certains traités, la taille des culées est décrite par des tracés d'hexagones inscrits dans l'arc. Cette méthode était très populaire et a donné des résultats positifs.
En Espagne, des théoriciens au XVIe siècle ont développé leurs propres idées sur le sujet, parmi eux Rodrigo Gil de Hontañón et plus tard Tomás Vicente Tosca[15]. Cependant, l'émergence de l'analyse des structures appareillées voûtées en pierre de taille se produit à la fin du XVIIe siècle. On peut affirmer que dans la seconde moitié du XVIIIe siècle la stabilité de l'arc construit en maçonnerie était suffisamment résolue pour des motivations pratiques et qu'il existait plusieurs méthodes suffisamment développées et des tables de dimensionnement publiées relativement simples. C'est le physicien italien Galileo Galilei qui a été l'un des premiers à découvrir que les fondements empiriques de la conception des arcs pouvaient avoir une cause physique[16] en précisant que la théorie de l'équilibre d'un arc pouvait se plier aux lois de la statique.
Théories scientifiques
[modifier | modifier le code]Le premier à émettre une théorie sur le fonctionnement d'un arc est Léonard de Vinci, il précise : « Il n’y aura pas de rupture de l’arche si la corde de l’arc ne touche pas l’arc interne. » Il a également formulé l’une des plus belles et élégantes définitions de l’arc : « L'arc n’est rien d’autre qu’une forteresse causée par deux faiblesses. L'arc dans les bâtiments est composé de deux quarts de cercle très faibles par eux-mêmes voulant tomber, et s'opposer à la ruine de l'autre, les deux faiblesses se transforment en une seule forteresse[17] », mais jusqu'en 1670, le problème n'est pas formulé en termes scientifiques.
Robert Hooke (1635-1703) mentionne l'arc à la fin d'un de ses livres A Description of Helioscopes, and Some Other Instruments, publié en 1676[note 1], sous la forme d'une anagramme en latin qui décrit l'arc comme ressemblant à une caténaire inversée : « Ut pendet continuum flexile, sic stabit contiguum rigidum inversum », qui signifie approximativement : « De même que pend un fil flexible, de même, en inversant, on trouve les pièces contiguës d'une arche[18]. Robert Hooke n'a pas fourni de son vivant, les traductions latines de ses anagrammes, celles-ci ont été données par son exécuteur testamentaire en 1705, deux ans après sa mort[19]. »
Robert Hooke conclut de cette même manière, juste après avoir collaboré avec Christopher Wren à la réalisation du dôme de la cathédrale Saint-Paul de Londres. Hooke se rend compte qu'un arc se soutient si une caténaire inversée est contenue dans son épaisseur. Bien que les deux architectes, Christopher Wren et Robert Hooke, aient eu connaissance des propriétés remarquables de cette courbe (« catenary curve »), ils étaient incapables à l'époque, d'en trouver une formulation mathématique exacte (qui n'est venue qu'en 1691 avec Jacques Bernoulli, Leibniz et Huygens). On retrouve dans l'esquisse pour la construction du dôme, datant de 1690[note 2], une « approximation » de la courbe de la chaînette renversée : cette courbe est une parabole cubique (voir la figure 2 du document en référence, et les trois courbes superposées). Le dôme est formé par le conoïde, décrit par la rotation de la demi-parabole cubique y=x3, sur l'axe des ordonnées[20].
De même, des années plus tard, le mathématicien David Gregory fournit une manière de dimensionner une culée, montrant que si dans la caténaire les forces poussent vers l'intérieur, dans l'arc d'une caténaire inversée, elles le font vers l'extérieur. Le mathématicien français Philippe de La Hire (1640-1718) a une approche différente dans son Traité de mécanique, essayant de trouver quel est le poids approprié des voussoirs pour améliorer la stabilité de l'arcade[21], employant pour la première fois un polygone funiculaire dans la description d'un arc, avec l'hypothèse initiale de non-résistance entre les voussoirs. Plus tard, en l'an 1712, il publie son mémoire sur la Construction des voûtes dans les édifices qui influence les générations postérieures de constructeurs européens comme dans les tables constructives des arcs de ponts élaborés par Jean-Rodolphe Perronet[22]. Ces tables seront populaires dans la construction empirique de ponts européens jusqu'à la moitié du XIXe siècle.
Dans deux mémoires publiés dans les Mémoires de l'Académie royale des sciences, en 1729 et 1730, Pierre Couplet de Tartereaux (1670-1743) étudie l'équilibre des voûtes en partant de l'hypothèse d'une simple rotation autour des arêtes de leurs voussoirs. Il étudie la stabilité de la voûte en la supposant constituée de quatre voussoirs égaux attachés ensemble par des charnières. Augustin Danyzy (1698-1777) fait des expériences en modèle réduit qui démontrent la validité de la théorie de Couplet sur le mode de renversement des voûtes.
En 1743, le physicien italien Giovanni Poleni est mandaté par le pape Benoît XIV pour examiner le dôme de la basilique Saint-Pierre de Rome, et effectuer la vérification statique de l'équilibre de la coupole, qui risquait de s'effondrer. Dans son rapport au pape, Memorie istoriche della Gran Coupola del Tempio Vaticano (publié en 1748), Poleni utilise le modèle de la caténaire[23] ainsi que les travaux du mathématicien écossais James Stirling.
Dans le dernier quart du XVIIIe siècle, avec l'arrivée de la révolution industrielle apparaissent quelques exemples d'arcs continus élaborés en fonte. Un des premiers est un arc de pont bâti en 1779, et dénommé « Iron Bridge » qui franchit la rivière Severn (Royaume-Uni) avec trente mètres de portée[24]. La fonte ouvre la voie à l'utilisation ultérieure, déjà au XIXe siècle, du fer forgé et avec elle la portée des ponts considérablement augmentée. Jean-Victor Poncelet a été l'un des premiers à vérifier que les arcs étaient des structures hyperstatiques (ou redondantes) dont la solution nécessite la résolution d'équations de compatibilité et une loi qui relie les déformations aux tensions.
L'ingénieur Pierre Couplet prend une hypothèse différente de La Hire et obtient de manière analytique une valeur minimale pour l'épaisseur d'un arc. Au-dessous de cette valeur, l'arc s'écroule. La description de la stabilité d'une arche la plus utilisée plus tard est faite par Charles-Augustin Coulomb en l'an 1773[25]. Dans son travail, il montre sept manières possibles de faire s'écrouler une arche. Entre 1830 et 1840, la théorie de la ligne de poussée est développée simultanément par divers chercheurs ingénieurs. L'un d'eux est Henry Moseley qui décrit la stabilité d'une arche[26]. Résultats perfectionnés par Jules Carvallo et Durand-Claye[27]. Les nouvelles théories, confrontées aux vieilles méthodes empiriques, montrent, bien que fondamentalement incorrectes, combien les résultats constructifs étaient étonnamment bons[28].
Avec l'apparition du béton et de l'acier au début du XXe siècle, la construction d'arcs continus cesse de se faire par juxtaposition de pièces de petite taille. Bientôt, des centaines de mètres de portée sont atteints dans les ponts, en raison de l'utilisation de ces matériaux de construction jusqu'à atteindre un millier de mètres dans le cas de ponts à haubans. À ce stade, les théories élaborées sur les arcs nécessitent de nouvelles recherches scientifiques. Dans cette ligne travaillent Kooharian (1952)[29] et Heyman (1966)[30]. Les arcs continus ne possèdent pas les propriétés mécaniques et structurelles des anciennes arches appareillées et leur théorie est beaucoup plus simple à appréhender.
Éléments et dimensionnement des arcs
[modifier | modifier le code]Traditionnellement, certains éléments constitutifs des arcs ont été dénommés. Dans le cas d'arcs construits avec des éléments d'usine, certaines dénominations sont utilisées dans la plupart des traités de construction.
-
Éléments d'une arche.
-
Arc de contrefort représenté par Eugène Viollet-le-Duc.
-
Parfois, l'arc est combiné comme un élément de renforcement constructif.
Éléments matériels constitutifs de l’arc
[modifier | modifier le code]Un arc est tout assemblage de pierre, de moellon ou de brique destiné à franchir un espace plus ou moins grand au moyen d'une courbe (ou par la rencontre de deux éléments courbes), reposant sur deux points d’appui, les piédroits, et destiné à couvrir une baie, une ouverture, ou une distance à l’intérieur d’une maçonnerie de mur plein (arc aveugle)[31]. On distingue de nombreuses sortes d'arc, en fonction de leur forme.
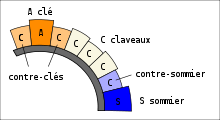
Jusqu'à l'apparition au XXe siècle des arcades continues, les arcs en pierre de taille ou en briques étaient composés de divers éléments et un vocabulaire architectural s'est mis en place qui s'est communiqué dans les différents traités de construction. Les principaux éléments qui composent une arche de pierre sont :
- les claveaux[note 3] ou voussoirs[note 4], pièces en forme de coin qui composent l'arche ou la voûte et qui se caractérisent par leur disposition radiale (dans son sens ancien, le claveau sert à fermer une plate-bande et le voussoir sert à fermer une arcade[32]). Les voussoirs des extrémités et qui reçoivent le poids de l'arche s'appellent « sommier[note 5] » (c'est le claveau/voussoir de départ). La partie interne d'un claveau/voussoir ou d'une arche/voûte s'appelle « intrados[note 6] » (ou « douelle[note 7] ») et son dos qui n'est pas visible à l'intérieur de la construction, se nomme « extrados[note 8] ». La coupe des voussoirs est la manière dont les voussoirs sont disposés par rapport à leur centre. Lorsque les voussoirs suivent les rayons du même centre, on parle d'arche radiale, bien que ce centre ne coïncide pas toujours avec le centre de l'arcade comme dans l'arc outrepassé wisigothique. Les voussoirs peuvent être placés horizontalement jusqu'à une certaine hauteur comme dans l'arche mozarabe ;
- la clef (clef d'arc, clef de voûte[note 9]) est le claveau ou voussoir central qui ferme l'arche ou la voûte. C'est le dernier placé au moment du coffrage, complétant le processus de construction de l'arche. La clé est généralement le plus grand segment et, pour assurer la stabilité de l'arc, le plus lourd. Les deux claveaux/voussoirs adjacents à la clef s'appellent « contre-clés » ou « contre-clefs » ;
- les reins : parties triangulaires des voûtes comprises entre la ligne de leur extrados, celle du prolongement de leurs pieds-droits et la ligne de niveau qui passe par leur sommet ; ces reins sont faits d'une maçonnerie que l'on nomme « remplissage des reins[33] » quand ils ne sont pas le lieu d'élégissements. Cette partie se nomme aussi « écoinçon », ou « tympan ». Toutefois, « tympan » peut aussi désigner l'espace semi-circulaire d'un portail, compris entre le linteau et les archivoltes un arc plein-cintre ou une voûte d'ogive.
Dimensions
[modifier | modifier le code]
L'arc en tas de charge utilise la forte résistance à la flexion sans rupture d'un certain type de pierres. Elles sont maçonnées en pilier avec, à partir d'une certaine hauteur, un léger décrochement en porte-à-faux sur l'assise inférieure de chaque assise horizontale. Des corniches symétriques au-dessus du vide sont constituées pour le franchir (des arcs-poids, des arches de pierres encastrées).
Un arc léger tient selon le principe de la compression. Les claveaux se tiennent mutuellement alors que leurs assises ne sont pas horizontales. L'arc n'est stable que lorsqu'il est complet. C'est pourquoi il est nécessaire de monter d'abord un échafaudage (souvent en bois) appelé cintre afin de créer une structure temporaire sur laquelle on peut placer les pierres ou claveaux. La clef d'arc est la dernière pierre posée, c’est-à-dire celle du milieu. C'est elle qui confère à l'arc sa stabilité.
L'arc repose sur deux appuis : les piédroits. On appelle « sommier » le claveau portant directement sur le piédroit, les contreclefs sont les claveaux sur lesquels s'appuie la clef. Il y a autant de claveaux de part et d'autre de la clef, donc autant de joints de part et d'autre de la clef, ce qui évite un tassement de l'arc dissymétrique.
On appelle « naissance » l'endroit où le sommier repose sur le piédroit. La naissance est aussi le commencement de sa courbure, formé par les premières assises en pierres ou en moellons ; dans le cas d'un arc, on parle de ligne de naissance, dans le cas d'une voûte, on parle de plan de naissance[34].
La largeur d'un arc se nomme « portée » et sa hauteur la « flèche » (prise verticalement entre la naissance et la clef, ou la hauteur de l'arc mesurée à partir de la ligne où il commence jusqu'à la clé). Le centre peut être supérieur ou inférieur à l'imposte, il peut y avoir plus d'un centre.
L'arc en accolade est un faux-arc très infléchi tracé à partir de deux centres intérieurs et de deux centres intérieurs, alternativement convexe et concave, couronnant un linteau monolithique ou composé de claveaux surmontant une porte ou une fenêtre. L'arc en doucine est formé de la même manière, mais en sens inverse[35].
L'arc peut présenter un ou plusieurs segments courbes, chaque segment correspondant à un centre différent, le centre de courbure.
Types d'arcs
[modifier | modifier le code]
Selon la forme géométrique de l'intrados et la forme générale de l'arc, il y a un grand nombre de dénominations d'arc. Chaque style architectural a été caractérisé par son propre type d'arche, chaque époque ou culture. Il est possible que le premier arc ait été l'arc en plein cintre (demi-cercle), duquel découlent les autres arcs. D'autres classifications découlent de la fonction structurelle ou décorative de l'arc (arc boutant, arc aveugle), arcs monumentaux (arc de triomphe), etc.
Arcs commémoratifs
[modifier | modifier le code]Les arcs commémoratifs sont les monuments érigés pour célébrer un événement de grande importance historique, généralement une victoire militaire. Originaires de la Rome antique, leur utilisation a été perpétuée jusqu'à aujourd'hui. Normalement, ce sont de grands monuments en pierre prismatiques, en forme de grande porte terminée par une forme arquée. La mission de l'arc dans ce cas est simplement ornementale. Ce type d'arches est généralement situé à l'entrée de villes importantes, ou capitales. Dans de nombreux cas, ils ont fonction de porte d'accès.
Arcs continus
[modifier | modifier le code]
Les arcs métalliques sont conçus selon des principes totalement différents des arcs en pierre. En effet, les métaux sont des matériaux qui peuvent résister à la fois à la traction et à la compression, contrairement aux constructions en pierre et autres matériaux céramiques, qui ne peuvent résister qu'à des compressions importantes.
La complexité des connaissances et des techniques de construction s'est accrue avec le temps, si bien que la spécialisation a été nécessaire. Pour ces raisons, les arcs structurants des grands travaux publics, tels que les ponts, sont considérés comme des arcs d'ingénierie. Dans certaines œuvres, traditionnellement architecturales, comme dans certains stades, vu la grande portée des arcs, il est nécessaire que l'ingénierie fournisse des solutions à l'architecture.
Il existe essentiellement deux types d'arcs métalliques :
- les arches métalliques rigides en treillis, essentiellement constituées par une multitude de barres jointes à leurs extrémités, travaillant soumises à des efforts axiaux de traction ou de compression le long de l'axe longitudinal des barres ;
- les arcs métalliques flexibles, formés par une pièce prismatique incurvée qui travaille principalement en flexion.
Typologie
[modifier | modifier le code]


Les arcs peuvent être classés en trois grandes catégories :
- les arcs plein cintre, formés par un demi-cercle ;
- les arcs surbaissés, ou en anse de panier, formés par un ovale une demi-ellipse, le grand diamètre à la base ; l'arc déprimé est une variante de l'arc surbaissé (l'arc est alors déprimé au point de former une ligne horizontale droite comme un linteau et recourbé aux deux bouts)[35].
- les arcs brisés (en lancette ou en tiers-point), formés de deux portions de cercle qui se croisent et donnent un angle curviligne plus ou moins aigu au sommet, suivant que les centres sont plus ou moins éloignés l'un de l'autre. On parle d'arc en tiers-point lorsqu'il est élevé sur un triangle équilatéral et formé par deux courbes ayant chacune leur centre à la naissance de l'arc de cercle qui lui est opposé. L'arc en lancette est élevé sur un triangle dont l'angle supérieur est plus aigu que les deux autres[35].
Les arcs plein cintre sont quelquefois surhaussés, qui un trompe-l'œil puisqu'il s'agit d'un arc plein cintre classique dont les impostes sont en dessous des naissances de l'arc. Les arcs peuvent être outrepassés, dits alors en fer à cheval, formant un demi cercle plus ou moins prolongé en dessous du diamètre[36]. Cette formule d'origine paléochrétienne est souvent utilisée dans les monuments islamiques. Il existe également des arcs bombés, lorsque le centre est au-dessous de la naissance. Les Persans ont introduit une forme d'arc angulaire, chaque côté comportant deux arcs de cercle tangents.
-
Vue perspective.
-
Arc plein cintre.
-
Arc parabolique.
-
Arc surbaissé (segmentaire).
-
Arc en anse de panier à 3 centres.
-
Arc en anse de panier à 5 centres (demi-ellipse).
-
Arc en plate-bande.
-
Arc Tudor.
-
Arc brisé en tiers-point.
-
Arc brisé en lancette.
-
Arc outrepassé ou arc en fer à cheval.
L'utilisation de l'arc en architecture commence dès l'Antiquité. Les civilisations égyptienne et babylonienne l'utilisaient principalement dans des structures souterraines. Mais pour franchir un espace important, seuls les linteaux et architraves étaient connus.
L’Égypte pharaonique bâtissait des voûtes à poussée dès la IVe dynastie, tant en brique crue qu'en pierre. Arc et voûte clavés étaient répandus dans le monde grec. En témoigne la remarquable tombe de Vergina datée de 336 av. J.-C. La technique du clavage arrive alors peu à peu en Italie. Les Grecs et les Étrusques y élaborent les premiers modèles connus des Romains qui font aboutir la technique à une maîtrise absolue. Des fouilles ont permis de déterminer que l'embouchure à triple rang emblématique, cloaca maxima, daterait du Ier siècle av. J.-C. au plus tôt, ce qui contredit l'origine étrusque de cette probable reconstruction. La porte de Jupiter de Faléries postérieure à 241 av. J.-C. est par contre un jalon sur[pas clair] dans l'histoire de l'origine des arcs clavés et rien ne permet de croire qu'il y en eût à Rome avant le IIIe siècle av. J.-C. Témoins de maîtrise technique, le pont Fabricius construit sur le Tibre en 62 av. J.-C. aligne deux arcades de 24,5 m qui forcent encore aujourd'hui l'admiration[37].
Jusqu'à la fin du XIe siècle, l'arc en plein cintre avec ses variétés est seul employé dans les constructions, sauf quelques rares exceptions. Quant aux arcs surbaissés que l'on trouve souvent dans les voûtes de l'époque romane, ils ne sont presque toujours que le résultat d'une déformation produite par l'écartement des murs, ayant été construits originairement en plein cintre.
C'est pendant le XIIe siècle que l'arc formé de deux portions de cercle (et que nous désignerons sous le nom d'arc en tiers-point, conformément à la dénomination admise pendant les XVe et XVIe siècles), est adopté successivement dans les provinces de France et dans tout l'Occident. Cet arc n'est en réalité que la conséquence d'un principe de construction complètement nouveau (la croisée d'ogives) ; d'une combinaison de voûtes que l'on peut considérer comme une invention moderne rompant tout à coup avec les traditions antiques. L'arc en tiers-point est toutefois employé en Orient plusieurs siècles avant d'apparaître en Occident[38]. Et il est probable que les Arméniens qui ont fui leur pays après la bataille de Manzikert sont partis pour certains en Occident, pour d'autres dans les vallées du Caucase où ils ont introduit de nouvelles manières de construire l'arc en tiers-point et la voûte en carène qui s'imposeront dans l'architecture cistercienne après être apparus à Cluny III[39].
L'arc en tiers-point disparaît avec les dernières traces de l'art du Moyen Âge, vers le milieu du XVIe siècle ; il est tellement inhérent à la voûte moderne qu'on le voit longtemps encore persister dans la construction de ces voûtes, alors que déjà, dans toutes les autres parties de l'architecture, les formes empruntées à l'Antiquité romaine étaient successivement adoptées. Les architectes de la Renaissance voulant définitivement exclure cette forme d'arc n'ont rien trouvé de mieux que d'y substituer, comme dans l'église Saint-Eustache de Paris, vers la fin du XVIe siècle, des arcs en ellipse, le petit diamètre à la base ; courbe désagréable, difficile à tracer, plus difficile à appareiller et moins résistante que l'arc en tiers-point.
Outre les dénominations précédentes qui distinguent les variétés d'arcs employées dans la construction d'édifices du Moyen Âge, on désigne les arcs par des noms différents, suivant leur destination[40] :
Usages
[modifier | modifier le code]L'usage le plus traditionnel d'une arche a été, depuis l'Antiquité, de créer un jour, une baie, une ouverture dans un mur et plus particulièrement sur la façade d'un bâtiment. En raison de sa capacité particulière à transformer la poussée verticale communiquée par la masse du bâtiment en composantes plus horizontales, il a été utilisé comme support, en même temps que forme d'ouverture des murs. Dans beaucoup de cas, son existence donne lieu à une fenêtre, à une porte ou un accès en général. Dans les contreforts des cathédrales, il a fonction de soutien. Son utilisation dans la construction de ponts (pont en arc) a été fondamentale[41]. L'utilisation d'ensembles d'arcs enchaînés dans une séquence s'appelle « portiques ».
Peu à peu, avec l'apparition de nouveaux matériaux de construction, l'utilisation de l'arche s'est réduite à un usage quasi-exclusif dans certains travaux de génie civil. Les arches sont actuellement employées dans de rares occasions, à usage décoratif et ornemental loin de leur fonction principale, et, dans certains cas, elles servent de monument commémoratif.
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- En p. 31, alinéa 2
- Esquisse du dôme (1690), conservée au British Museum, référence : PD 1881-6-11-203
- Claveau : toutes pierres taillées en forme de coin et qui servent à construire une plate-bande, une architrave. Claveau à crossette : claveau dont la tête est retournée avec les assises de niveau. Claveau à joint dérobé : claveau dont le joint du parement de face est droit et dont celui du derrière est oblique. Dans Morisot (Maçonnerie) 1814, p. 19.
- Voussoir : pierre taillée en forme de pyramide tronquée qui sert à former le cintre d'une voûte, d'une arcade. Voussoir extradossé : voussoir dont la tête est de niveau et qui forme l'extrados de la voûte. Voussoir à branche : voussoir qui a deux branches en fourche pour faire liaison avec le pendentif d'une voûte d'arête. Voussoir à crossette : voussoir dont la partie supérieure fait un angle pour se raccorder avec une assise de niveau. Dans Morisot (Maçonnerie) 1814, p. 101.
- Sommier : première pierre de chaque côté d'un arc ou d'une plate-bande, qui se trouve à l'aplomb d'un pied-droit ou sur une colonne, un pilastre, etc. Dans Morisot (Maçonnerie) 1814, p. 88.
- intrados : surface intérieure ou concave d'une voûte, d'un arc, d'un voussoir. Dans Morisot (Maçonnerie) 1814, p. 44.
- Douelle : parement intérieur d'une voûte ou d'un voussoir, que l'on nomme aussi intrados. Dans Morisot (Maçonnerie) 1814, p. 27.
- Extrados : surface convexe extérieure d'une voûte qui est régulière, comme la surface concave intérieure est intrados ; Extradossé : surface extérieure d'une voûte qui est de niveau dans toute sa surface, c'est-à-dire que tous les voussoirs sont coupés également, en sorte que le parement extérieur est aussi uni que celui de la douelle. Dans Morisot (Maçonnerie) 1814, p. 34.
- Clé de voûte, clé d'arc, clé de plate-bande : dernier voussoir ou claveau que l'on pose au sommet d'une voûte, d'un arc ou d'une plate-bande, pour les fermer et les bander. Dans Morisot (Maçonnerie) 1814, p. 19.
Références
[modifier | modifier le code]- Muy interesante, 2010, no 8, p. 22.
- (en) Mann Herbert A., A History of Civil Engineering : An Outline from Ancient to Modern Times, MIT Press, , 1re éd. (ISBN 978-0-262-69005-8).
- (en) Jacques Heyman, Beams and Framed Structures, Elsevier, , 2e éd., 136 p. (ISBN 978-0-08-017946-9).
- (es) Santiago Huerta Fernández, Árcos, Bóvedas y Cúpulas : geometría y equilibrio en el cálculo tradicional de estructuras de fábrica, Madrid, Instituto Juan de Herrera, , 1re éd., 623 p. (ISBN 978-84-9728-129-4, BNF 40077701).
- (de) J. E. Silberschlag, Ausfürlische Abhandlung der Hydrotechnik oder Wasser bauns, Leipzig, .
- H. Parland, Basic Principies of the Structural Mechanics of Masonry : A Historical Review, vol. 2, International Journal of Masonry Construction, , p. 49.
- (en) Anthony Kooharian, « Limit Analysis of Voussoir (Segmental) and Concrete Archs », Journal American Concrete Institute, vol. 49, no 12, , p. 317-328.
- Roland Besenval, Technologie de la voûte dans l'Orient ancien, Paris, Recherche sur les civilisations, (ISBN 978-2-86538-082-4).
- (en) Kurrer Karl-Eugen, The history of the theory of structures : from arch analysis to computational mechanics, Berlin, Ernst & Sohn Verlag, , 1re éd., 848 p. (ISBN 978-3-433-01838-5, BNF 42002132).
- (es) Amparo Graciani García, La técnica de la arquitectura medieval, Universidad de Sevilla, , 1re éd..
- (es) Ilustración de Madrid : revista de política, ciencias, artes y literatura, vol. 3, Madrid, Imp. El Imparcial, , « El puente del diablo », p. 55.
- (en) H. Hotton, The Elements of Architecture, Londres, .
- (en) Frank Woodward Skinner, Types and Details of Bridge Construction : Arch spans, New York, McGraw Publishing Company, , 1re éd., p. 162.
- (es) Jacques Heyman, La ciencia de las estructuras, Madrid, Instituto Juan de Herrera, , 1re éd., 134 p. (ISBN 978-84-95365-98-9).
- Santiago Huerta Fernández, Diseño estructural de arcos, bóvedas y cúpulas en España, ca. 1500-ca. 1800, Madrid, Escuela Técnica Superior de Arquitectura de Madrid. E.T.S. Arquitectura (UPM), .
- (en) Joseph Gwilt, A Treatise on the Equilibrium of Arches, Londres, Priestley & Weale, , 1re éd..
- (it) Ingegneria con Criterio, « L’arco in muratura – Definizioni, : L'arc en maçonnerie », sur ingegneriaconcriterio.it (consulté le ).
- (en) Robert Hooke, « A Description of Helioscopes, and Some Other Instruments », sur e-rara.ch, (consulté le ).
- (en) Linda Hall Library of Science, Engineering & Technology, « Hooke, Robert (1635-1703) », sur civil.lindahall.org (consulté le ).
- (en) Snezana Lawrence, « The Dome that Touches the Heavens (2014) », sur citeseerx.ist.psu.edu, (consulté le ).
- De La Hire, Traité de mécanique, où l'on explique tout ce qui est nécessaire dans la pratique des arts, et les propriétés des corps pesants lesquelles ont eu plus grand usage dans la physique, Paris, Imprimerie royale, , 1re éd..
- Jean-Rodolphe Perronet, Antoine de Chézy, Pierre Charles Lesage (coll.), « Formule générale pour déterminer l'épaisseur des piles et culées des arches des ponts, soit qu'elles soient en plein cintre ou surbaissées », Recueil de divers mémoires extraits de la Bibliothèque impériale des ponts et chaussées à l'usage de MM. les ingénieurs, Firmin Didot, 1810, books.google.ca (consulté le 1er mai 2019).
- (it) Giovanni Poleni, « Memorie istoriche della gran cupola del tempio vaticano : Livre premier, figure XIV », sur e-rara.ch, (consulté le ).
- Pérez-Fadón Martínez, « Arcos: Evolución y tendencias futuras », Revista de Obras Públicas, Santiago, 2005 (Madrid) 152 (3451), 7-24, Archivado desde el original el 19 de mayo de 2014 (consulté le 28 octobre 2011).
- Charles-Augustin de Coulomb, « Essai sur une application des règles de maximis et minimis à quelques problèmes de statique relatifs à l'architecture », Mémoires de mathématique et de physique, présentés à l’Académie royale des sciences par divers savants et lus dans ses assemblées, Paris, 1773, 7[Quoi ?], p. 343-438.
- H. Moseley, « On the equilibrium of the arch », Cambridge Pbilosophical Transactions (lire le 9 décembre 1833), 1835, 5[Quoi ?], p. 293-313.
- J. Carvallo, « Étude sur la stabilité des voutes », Annales des ponts et chaussées, 1853, vol. 1, 2e sem., p. 1.
- H. I. Dorn, The Art of Building and the Science of Mechanics: An study of the union of theory and practice in the early history of structural analysis in England, 1re édition, Princeton University, 1970, p. 50.
- Anthony Kooharian, « Limit analysis of voussoir (segmental) and concrete archs », Journal American Concrete Institute, 1952, vol. 49, no 12, p. 317-328.
- Jacques Heyman, The Stone Skeleton: Structural engineering of masonry architecture, University of Cambridge, 1997 (ISBN 9780521629638).
- Dictionnaire raisonné de l’architecture française du XIe au XVIe siècle, t. 1, « Arc ».
- Littré. Dictionnaire de la langue française, 1873, t. 1.
- Morisot (Maçonnerie) 1814, p. 80.
- Joseph Alphonse Adhémar, Cours de mathématiques. Traité de la coupe des pierres, deuxième édition revue et augmentée, 1840.
- Claude Augé, Nouveau Larousse illustré, Paris, Larousse, , p. 44, 408
- Adelbert Van de Walle, Comment reconnaître le style des édifices, Paris, Éditions de Montsouris, , p. 39, 40
- Adam 2011, p. 163-177.
- Eugène Lefèvre-Pontalis, « L'arc brisé et ses applications méthodiques dans l'Île-de-France », Comptes rendus des séances de l'Académie des inscriptions et belles-lettres, 38e année, no 3, 1894, p. 177-178, DOI .10.3406/crai.1894.70402.
- Henri Stierlin, Turquie. Des Seldjoukides aux Ottomans, Taschen, 2002, 240 p. (ISBN 978-3822818015).
- Eugène Viollet-le-Duc.
- (es) [PDF] Santiago Pérez-Fadón Martínez, « Arcos: Evolución y tendencias futuras », Revista de Obras Públicas, Santiago, 2005 (Madrid) 152 (3451), p. 7-24 (lire en ligne) (consulté le 3 décembre 2019).
Annexes
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- Jean-Pierre Adam, La Construction romaine : matériaux et techniques, Grands Manuels picards, , 6e éd., 367 p. (ISBN 978-2-7084-0898-2).
- J.-M. Morisot, Tableaux détaillés des prix de tous les ouvrages du bâtiment, Carilian, (lire en ligne).
- Eugène Viollet-le-Duc, Dictionnaire raisonné de l'architecture française du XIe au XVIe siècle, tome 1 : « Arc ».
Articles connexes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]
- Ressource relative aux beaux-arts :
- Notices dans des dictionnaires ou encyclopédies généralistes :