قضیه تالس
این مقاله نیازمند ویکیسازی است. لطفاً با توجه به راهنمای ویرایش و شیوهنامه، محتوای آن را بهبود بخشید. |

قضیه تالس یکی از قضایای مهم در هندسه مقدماتی است که میگوید: اگر دو خط راستِ موازی با یکدیگر، دو خط متقاطع را قطع کنند، آنگاه بر روی آن دو خط متقاطع پاره خطهای متناسب ایجاد میشود.
قضیه تالس نیز مانند سایر قضایا هندسی دو شرطی است (عکس آن برقرار است) بنابراین درعکس قضیه تالس یا شرط دوم آن اگر خطی از دو ضلع مثلث، پاره خطهای متناسب ایجاد کند آن خط موازی ضلع سوم است. (BC موازی با DE)
تاریخچه
[ویرایش]مصریان باستان
[ویرایش]
هزار و سیصد سال قبل از تولد تالس مصریان باستان قضیهٔ تالس را میدانستند؛ درواقع در راه حل مسئلهٔ شماره ۵۳ پاپیروس رایند از معادل قضیهٔ تالس استفاده میشود.[۱]
یونانیان باستان
[ویرایش]با توجه به منابع تاریخی یونان باستان، تالس ریاضیدان یونانی با استفاده از این قضیه توانست ارتفاع هرم خئوپس را به دست آورد.[۲]
قضیهٔ دوم مقالهٔ ششم اصول اقلیدس به اثبات قضیهٔ تالس و عکس آن میپردازد.
اثبات و تعمیم قضیه تالس
[ویرایش]بیان قضیه و اثبات در اصول اقلیدس
[ویرایش]اگر خط راستی موازی با یکی از اضلاع مثلث رسم شود، دو ضلع دیگر را به یک نسبت میبرد.(قضیه ۲ مقالهٔ ششم)
"فرض میکنیم DE موازی با BC یکی از اضلاع مثلث ABC رسم شدهاست. میخواهیم اثبات کنیم نسبت BD به AD مثل نسبت CE است به AE.
E را به B و D را به C وصل میکنیم؛ بنابراین مساحت مثلث BDE با مساحت مثلث CDE مساوی است؛ زیرا هر دو دارای یک قاعدهٔ DE هستند و رأسهای آنها بر خط راست BC، موازی با قاعدهٔ DE قرار دارد؛"

"از آن جایی که نسبتهای کمیتهای متساوی به یک کمیت با هم مساوی اند پس نسبت مساحت مثلث BDE به مثلث ADE مثل نسبت مساحت مثلث CDE است به مثلث ADE. از طرفی نسبت مساحت مثلث BDE به مساحت مثلث ADE، مثل نسبت BD است به DA؛ زیرا دارای یک ارتفاع اند که از E بر AB عمود میشود و نسبت آنها به یکدیگر مثل نسبت قاعدههای آنهاست. بهطور مشابه نسبت مساحت مثلث CDE به مساحت مثلث ADE مثل نسبت CE است به EA. بنابراین نسبت BD به DA نیز مثل نسبت CE است به EA."[۳]
تعمیمهای قضیه تالس
[ویرایش]اگر خطی دو ضلع مثلثی را در دو نقطه قطع کند و با ضلع سوم آن موازی باشد، مثلثی پدید میآید که اندازهٔ ضلعهای آن با اندازهٔ مثلث اصلی متناسب است.
یعنی:
تعمیم اول
[ویرایش]با استفاده از ترکیب نسبت در صورت در عبارت ، عبارت اثبات میشود:
تعمیم دوم
[ویرایش]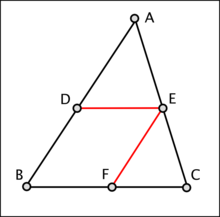
از نقطهٔ E پاره خطی موازی با AB رسم میکنیم EF با BA موازی است پس طبق تعمیم اول قضیهٔ تالس نسبت CE به EA برابر نسبت CF است به FB با استفاده از ترکیب در صورت ثابت میشود که نسبت AC به AE برابر نسبت BC به BF است، از طرفی میدانیم چهار ضلعی BDEF متوازی الاضلاع است پس پاره خط DE با پاره خط BF برابر است. پس میتوان نتیجه گرفت نسبت AC به AE برابر BC به BF است.
اثبات عکس قضیه در اصول اقلیدس
[ویرایش]اگر ضلعهای مثلثی به یک نسبت بریده شده باشند، خط راست واصل بین نقطههای بریدگی با ضلع سوم موازی است.
باز فرض میکنیم در مثلث ABC ضلعهای AB و AC به یک نسبت قطع شدهاند، به طوری که نسبت BD به DA مثل نسبت CE به EA است؛ و فرض میکنیم D به E وصل شدهاست. میخواهیم اثبات کنیم DE با BC موازی است. در همان شکل، چون نسبت BD به DA مثل نسبت CE است به EA اما نسبت BD به DA، مثل نسبت مساحت مثلث BDE است به مثلث ADE، و، نسبت CE به EA، مثل نسبت مساحت مثلث CDE است به مثلث ADE، بنابراین، نسبت مساحت مثلث BDE به مثلث ADE هم، مثل نسبت مساحت مثلث CDE است به مثلثADE. لذا نسبت مساحتهای هر یک از مثلثهای BDE و CDE به ADE، یکی هستند، بنابراین مساحت مثلث BDE با مثلث CDE مساوی است؛ و قاعده هر دو آنها DE است. اما مثلتهای متساوی که یک قاعده داشته باشند رأسهای آنها نیز بر خط راستی موازی با قاعده قرار دارند؛ بنابراین DE با BC موازی است.[۳]
اثبات به کمک بردار
[ویرایش]برای اثبات ابتدا فرض کنیم:

بنابراین:
ولی و بردارهایی در راستا و جهتهای مختلف اند، پس مجموع آنها نمیتواند صفر شود مگر آنکه:
و در نتیجه و از آنجا حکم ثابت میشود.[۴]
اثبات قضیهٔ تالس در فضای سه بعدی
[ویرایش]
صفحههای موازی، روی دو خط که آنها را قطع میکنند، پاره خطهای متناسب ایجاد میکنند.
با فرض آن که صفحه Q بین دو صفحه P و R قرار دارد، خط 'AC را رسم میکنیم. این خط صفحه Q را در نقطه ای مانند M قطع میکند. صفحه شامل دو خط متقاطع AC و 'AC را T و صفحه گذرنده از دو خط متقاطع 'AC و 'A'C را S مینامیم، داریم: صفحه T دو صفحه موازی Q و R را قطع کردهاست، بنابراین فصل مشترکها موازی هستند یعنی 'BM||CC، در نتیجه در مثلث 'ACC با توجه به قضیه تالس میتوان نوشت:
همچنین صفحه S دو صفحه موازی P و Q را قطع کردهاست، بنابراین فصل مشترکها موازی هستند یعنی 'B'M||AA، در نتیجه در مثلث 'ACC با توجه به قضیه تالس میتوان نوشت:
اکنون با توجه به دو رابطهٔ بالا داریم:
البته باید توجه داشت که عکس قضیهٔ تالس در فضا لزوماً برقرار نیست.[۵]
مفاهیم مرتبط
[ویرایش]مثلثهای متشابه
[ویرایش]
قضیهٔ تالس رابطهٔ تنگاتنگی با مفهوم تشابه دارد. در واقع قضایای مثلثهای متشابه به کمک قضیهٔ تالس اثبات میشوند؛ مثلاً با منطبق کردن گوشههای دو مثلث که زوایای یکسانی دارن، میتوان با توجه به موازی بودن دو ضلع پس از انطباق و استفاده از قضیهٔ تالس، متناسب بودن اضلاع دو مثلث را اثبات کرد.
ضرب اسکالر در فضای برداری
[ویرایش]در یک فضای برداری نُرمیده، با کمک اصول موضوعهٔ ضرب اسکالر (مشخصاً و )
میتوان قضیهٔ تالس را به دست آورد.

کاربردها
[ویرایش]به دست آوردن ارتفاع هرم خئوپس
[ویرایش]توضیح زیر استفاده از قضیهٔ تالس برای تعیین ارتفاع هرم خئوپس را شرح میدهد. البته این کار اصلی تالس -که ازبین رفتهاست- را بازگو نمیکند.

ابتدا تالس طول ضلع قاعدهٔ هرم و میله را اندازهگیری میکند. سپس همان موقع طول سایهٔ میله و سایهٔ هرم را اندازهگیری میکند؛ و دادههای زیر به دست میآید:

- طول ارتفاع میله: 1.63 m
- طول سایهٔ میله: 2 m
- طول ضلع مربع قاعدهٔ هرم: 230 m
- طول سایهٔ هرم: 65 m
با کمک دادههای بالا میتوان اطلاعات زیر را به دست آورد: حالا با دانستن B , A و c میتوان از قضیه تالس استفاده کرد. و مقدار D همان ارتفاع هرم میباشد.
ضرب دو پاره خط و پیدا کردن مقدار معکوس پاره خط
[ویرایش]سه مسئلهٔ معروف در هندسه مقدماتی وجود دارد که یونانیان باستان در بحث ترسیم با پرگار و ستاره آن را مطرح کردند.[۶]
دو هزار سال بعد در قرن نوزدهم میلادی با استفاده از جبر مجرد غیرممکن بودن این ترسیمها با پرگار و ستاره مشخص شد. برای بررسی ساختارهای ترسیم پذیر اطمینان یافتن از این موضوع مهم است که با دوخط داده شده خط دیگری میتوان رسم کرد که مقدار آن برابر حاصل ضرب دو خط اولیه باشد (ترسیم حاصل ضرب دو خط) و همینطور نشان دادن اینکه برای هر پاره خط به طول پاره خط دیگری میتوان ترسیم کرد که اندازهٔ آن باشد (ترسیم معکوس یک پاره خط). با استفاده از قضیهٔ تالس میتوان نشان داد که هر دو ساخت ممکن است.
ترسیم حاصلضرب
 |
ترسیم معکوس یک خط
 |
تقسیم پاره خط به نسبت دلخواه برای تقسیم پاره خط داده شدهٔ با نسبت به , نیم خطی را با زاویهٔ دلخواه از رسم میکنیم. بر روی نیم خط ساخته شده نقطه با فاصلهٔ یکسان قرار میدهیم، سپس خط گذرنده از آخرین نقطهٔ ساخته شده و نقطهٔ رسم میکنیم و در ادامه خط دیگری از امین نقطه و موازی با خط قبلی رسم میکنیم حالا پاره خط به نسبت خواسته شده تقسیم میشود. تصویر مقابل پاره خط را نشان میدهد که با نسبت به تقسیم شدهاست.[۷] |
 |
منابع
[ویرایش]- ↑ https://afrolegends.com/2016/11/23/the-rhind-papyrus-or-advanced-ancient-egyptian-mathematics/
- ↑ خطای یادکرد: خطای یادکرد:برچسب
<ref> غیرمجاز؛ متنی برای یادکردهای با نامmactutorوارد نشده است. (صفحهٔ راهنما را مطالعه کنید.). - ↑ ۳٫۰ ۳٫۱ https://mathcs.clarku.edu/~djoyce/java/elements/bookVI/propVI2.html
- ↑ هندسه(3) پایهٔ دوازدهم دورهٔ دوم متوسطه شابک ۹۸۷−۹۶۴−۰۵−۳۱۱۳−۶
- ↑ «نسخه آرشیو شده» (PDF). بایگانیشده از اصلی (PDF) در ۲۳ فوریه ۲۰۱۴. دریافتشده در ۷ مارس ۲۰۲۰.
- ↑ خطای یادکرد: خطای یادکرد:برچسب
<ref> غیرمجاز؛ متنی برای یادکردهای با نامKunzوارد نشده است. (صفحهٔ راهنما را مطالعه کنید.). - ↑ خطای یادکرد: خطای یادکرد:برچسب
<ref> غیرمجاز؛ متنی برای یادکردهای با نامOstermannوارد نشده است. (صفحهٔ راهنما را مطالعه کنید.).
- ↑ No original work of Thales has survived. All historical sources that attribute the intercept theorem or related knowledge to him were written centuries after his death. Diogenes Laertius and Pliny give a description that strictly speaking does not require the intercept theorem, but can rely on a simple observation only, namely that at a certain point of the day the length of an object's shadow will match its height. Laertius quotes a statement of the philosopher Hieronymus (3rd century BC) about Thales: "Hieronymus says that [Thales] measured the height of the pyramids by the shadow they cast, taking the observation at the hour when our shadow is of the same length as ourselves (i.e. as our own height).". Pliny writes: "Thales discovered how to obtain the height of pyramids and all other similar objects, namely, by measuring the shadow of the object at the time when a body and its shadow are equal in length.". However Plutarch gives an account, that may suggest Thales knowing the intercept theorem or at least a special case of it:".. without trouble or the assistance of any instrument [he] merely set up a stick at the extremity of the shadow cast by the pyramid and, having thus made two triangles by the intercept of the sun's rays, … showed that the pyramid has to the stick the same ratio which the shadow [of the pyramid] has to the shadow [of the stick]". (Source: Thales biography of the MacTutor, the (translated) original works of Plutarch and Laertius are: Moralia, The Dinner of the Seven Wise Men, 147A and Lives of Eminent Philosophers, Chapter 1. Thales, para.27)
- ↑ Kunz, Ernst (1991). Algebra (به آلمانی). Vieweg. pp. 5–7. ISBN 3-528-07243-1.
- ↑ Ostermann, Alexander; Wanner, Gerhard (2012). Geometry by Its History. Springer. pp. 7. ISBN 978-3-642-29163-0. (online copy, p. 7, در گوگل بوکس)









![{\displaystyle {\begin{array}{lcl}{\frac {CE}{AE}}={\frac {CF}{BF}}\Rightarrow {\frac {CE}{AE}}+1={\frac {CF}{BF}}+1\Rightarrow \\{\frac {AC}{AE}}={\frac {BC}{BF}}{\xrightarrow[{}]{BF=DE}}{\frac {AC}{AE}}={\frac {BC}{BF}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2880ca82b4e28cc81ec271797fe818fb8eb6932d)

























