Koniko

Koniko edo sekzio koniko bat kono bat plano baten bitartez ebakitzean lortzen den kurba da.
Hitzaren jatorria
[aldatu | aldatu iturburu kodea]Koniko hitzaren lehen definizioa Antzinako Grezian sortu zen K.a 340 urtean eta kono zirkular baten sekzio zuzen[1] gisa definituak izan ziren. Hiperbola, parabola eta elipse izenak Apolonio de Pergen omenez dira.
Gaur egun, koniken sekzio hauek modu ezberdinetan definitzen dira; definizio hauek matematikako adar ezberdinetatik datoz: geometria analitikotik, geometria proiektibotik ...
Historia
[aldatu | aldatu iturburu kodea]Menekmo
[aldatu | aldatu iturburu kodea]Ustez, Menekmok (K.a. 320), matematikari grekoak, sekzio konikoaren lehen definizioa eman zuen, kuboa bikoizteko problema[2] [3]ebazteko saiakeran. Ez zuten iraun, ez berak egindako lanak, ez kurba horiei erreferentzia egiteko izenek. Definizio hori gaur egun erabiltzen denaren ezberdina da. Konoak honela definitzen ziren: triangelu angeluzuzen bat bere kateto baten (konoaren ardatza) inguruan biratzean hipotenusak (konoaren zuzen sortzailea) sortzen duen gainazala. Konoaren ardatzaren eta zuzen sortzailearen arteko angeluaren arabera, hiru kono mota ezberdintzen ziren. Beraz, konoaren zuzen sortzailearekiko perpendikularra den plano bat hiru kono motekin ebakiz konikoak lortzen ziren: angeluaren bikoitza zorrotza bazen, elipse bat lortzen zen; angeluaren bikoitza zuzena bazen parabola bat lortzen zen; eta angeluaren bikoitza kamutsa bazen hiperbola lortzen zen.[4]
Euklidesek (K.a. 300) konikoei buruzko lau liburu idatzi zituen, baina galdu dira.[5] Arkimedesek (K.a. 212) sekzio konikoak aztertu zituen eta parabolak mugatzen duen azalera kalkulatu zuen. Arkimedes konikoekin erlazionatutako gorputzen azalera eta bolumena kalkulatzean interesatuta zegoen; bere lanaren zati bat "Konoideei eta Esferoideei buruz" liburuan irauten du.
Apolonio
[aldatu | aldatu iturburu kodea]Antzinako Grekoek konikoei buruz egindako azterketan, aurrerapen handiena Apolonio Pergakoak (K.a. 190) egin zuen; zortzi liburu idatzi zituen. Apoloniok Menekmok emandako definizioarekin bat zetorren definizioa eman zuen, gaur egun erabiltzen dena. Lehenengo definizioak ez zuen balio zirkulua definitzeko, aldiz, Apoloniok emandakoak bai. Horregatik, Apoloniok zirkulua konikotzat hartu zuen; gaur egun, zirkulua ez da konikotzat hartzen. Apoloniok hiperbola, parabola eta elipse izenak erabili zituen.
Pappus Alexandriakoak (K.o. 350) fokuaren garrantzia helarazi zuen.
Al-Kuhi
[aldatu | aldatu iturburu kodea]1000. urtean, Al-Kuhi matematikari islamiarrak sekzio konikoak marrazteko instrumentua deskribatu zuen lehen aldiz.[6]
Omar Khayyám
[aldatu | aldatu iturburu kodea]Apolonioren lana arabiarrera itzuli zuen, are gehiago, bere lanaren zati handi batek iraun du bertsio arabiarrean. Omar Khayyam Persiarrak sekzio konikoak erabili zituen ekuazio aljebraikoak ebazteko.[7]
Europa
[aldatu | aldatu iturburu kodea]Johannes Keplerrek konikoen teoria jarraitutasun printzipioaren bidez zabaldu zuen, geroago limitearen kontzeptuan erabilgarria izango zena.[7]
Girard Desarguesek eta Blaise Pascal-ek konikoen teoria garatu zuten, geroago geometria proiektiboa izendatuko zen arloaren oinarriak erabiliz. Hain zuzen ere, Pascalek hexagrammum mysticum izenarekin ezagutzen den teorema aurkeztu zuen, eta honen ondorioz konikoen beste propietate asko ondoriozta daitezke.
René Descartesek eta Pierre Fermat-ek geometria analitikoa aplikatu zuten sekzio konikoen azterketan. Horrek konikoen problema geometrikoak problema aljebraikoetan bilakatzen zituen. Hala ere, John Wallis-ek, 1655eko Tractatus de sectionibus conicis tratuan, sekzio konikoak bigarren mailako ekuazio gisa definitu zituen.
Lehenago idatzita, baina beranduago argitaratua, Jan de Witten Elementa Curvarum Linearum liburuak Keplerren teoria eta ekuazio aljebraikoak jasotzen ditu. Lan hau gaiari buruzko lehen liburutzat hartzen da.
Koniko motak
[aldatu | aldatu iturburu kodea]Sekzio koniko desberdinak lor daitezke, konoaren ardatzarekiko plano ebakitzaileak duen maldaren () eta konikotasun-angeluaren () arteko erlazio desberdinen arabera. Besteak beste:
- : hiperbola (berdea)
- : zirkunferentzia (elipsearen kasu partikularra) (horia)
- : triangeluarra
Plano ebakitzailea konoaren erpinetik pasatzen bada, ebakidurari koniko endekatu deritzo, eta hau froga daiteke:
- denean, ebakidura puntu bakarra da, erpina bera.
- denean, ebakidura konoaren zuzen sortzaile bat da (planoa konoarekiko ukitzailea izango da).
- denean, ebakidura konoaren erpinean elkar ebakitzen duten bi zuzenek osatzen dute.
- denean, zuzenek osaturiko angelua handituz joango da txikitu ahala. Planoak konoaren erpina barne duenean .


Koniken bigarren mailako ekuazio orokorrak
[aldatu | aldatu iturburu kodea]Definizioa
[aldatu | aldatu iturburu kodea]Bigarren mailako ekuazio orokorra edota ekuazio koadratikoa, hurrengo itxurako ekuazio bat da: .
x eta y aldagaiak dira eta A, B, C, D, E, F konstanteak. Behintzat, A, B edo C ez nuluak izanik.
Alde batetik, elipseek, parabolek eta hiperbolek ekuazio hori betetzen dute; ondorioz, sekzio konikoak dira. Bestetik, badaude bigarren mailako ekuazio batzuk sekzio konikoak ez direnak: adibidez, puntu bat, bi zuzen edota zuzen bat irudikatzen dutenak.[8]
Parametro konikoak
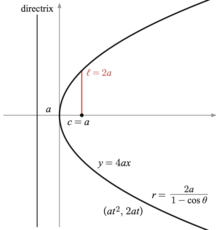
[aldatu | aldatu iturburu kodea]Ardatz nagusia: elipseen edo hiperboleen fokuak lotzen dituen zuzena da; haren erdiko puntua konikaren zentroa da. Parabolak ez du zentrorik.
Eszentrikotasun lineala: fokutik zentrora dagoen distantzia.
Latus rectum: fokutik ardatz nagusiarekiko perpendikularra den zuzen bat marraztean, konikoa mozten duen bi punturen arteko distantzia.
Foku parametroa: fokutik dagokion zuzentzailera dagoen distantzia.
Elipsearen ardatz nagusia: elipse baten ardatz luzeena da.

Elipsearen ardatz txikia: elipse baten ardatz motzena.
| Konikoa | Ekuazio konikoa |
|---|---|
| Zirkulua | |
| Elipsea | |
| Parabola | |
| Hiperbola |
Ekuazio horiek idazteko, koordenatu kartesiarrak erabiltzen dira. Ekuazio horiek guztiak koordenatu polarren bidez adieraz daitezke eta, hurrengo grafikoetan ikusi daitezkeen ekuazio orokorrak lortzen dira.
Grafikoak


Ekuazio kartesiar orokorra
[aldatu | aldatu iturburu kodea],
non baita diskriminatzailea.
Matrizialki:
Kalkulua egiteko determinantea kalkulatu behar da.
Diskriminatzailearen arabera ekuazio ezberdinak sailkatzen dira:
- B2-4AC < 0: elipsea
- A=C eta B=0 bada, zirkunferentzia.
- B2-4AC > 0: hiperbola.
- A+C = 0 bada, hiperbola errektangularra.
- B2-4AC = 0: parabola.
Ezaugarriak
[aldatu | aldatu iturburu kodea]Planoko bi puntuk zuzen bat definitzen duten bezala, bost puntuk koniko bat definitzen dute. Formalki, planoko bost puntu hartuta, horietako hiru (edozein) lerrokatuta ez egonik, existituko da koniko ez-endekatu bat bost puntu horietatik pasatzen dena eta, gainera, bakarra dena. Bost puntu horietatik hiru lerrokatuta badaude, orduan konikoa endekatua izango da eta ez du zertan bakarra izan.
Planoko lau puntu hartuz, koniko bat defini daiteke lehen hiru puntuetatik pasatzen dena eta zentro gisa laugarren puntua duena. Hau da, koniko bat definitzeari dagokionez, kurbako bi puntu ezagutzea zentroa ezagutzearen baliokidea da.
Planoko punturekin eta zuzenekin ere, defini daiteke koniko bat baldin eta . Kasu horretan, puntuetatik pasatzen den eta zuzen ukitzaile dituen konikoa izango da.
Planoko puntu bat konikoarekiko ukitzaile den zuzen bakarrean badago, puntua konikoan egongo da; puntua konikoarekiko ukitzaileak diren bi zuzenetan badago, puntua kanpoko puntua izango da; eta puntua ez badago konikoarekiko ukitzailea den zuzen batean ere, barruko puntua izango da.
Sekzio koniko guztiek islatze-propietatea betetzen dute; honela idatz daiteke: konikoko foku batetik datozen izpi guztiak, konikoan islatzean, beste fokurantz joaten dira. Era berean, konikoan islatu ondoren foku baterantz doazen izpiak beste fokutik etortzen dira. Parabolaren kasuan, bigarren fokutzat infinitua jotzen da, horrela, islapen-izpiak paraleloak dira.
Pascal-en teoremak koniko ez-endekatu batean dauden sei puntu hiru puntu lerrokaturekin erlazionatzen ditu. Pappus-en teorema koniko endekatuetan aplikatzen den teorema da.
Koniko ez-endekatu guztiak lauak dira; hau aplikazio askotarako garrantzitsua da; adibidez, aerodinamikarako.
Aplikazioak
[aldatu | aldatu iturburu kodea]Kurba konikoak astronomian oso garrantzitsuak dira, hainbat fenomeno deskribatzen laguntzen dutelako. Adibidez, grabitate indarraren mende dauden bi gorputzen arteko interakzioaren azterketan: haien gorputzen masa-zentroa mugimenduan ez badago, kurba konikoek egindako ibilbideek sekzio konikoak deskribatzen dituzte; elkarrengandik nahiko hurbil badaude, elipseak irudikatuko dituzte, eta bestela, parabola edota hiperbolak.
Aerodinamikan edota industrian duten aplikazioa ere handia da. Gaur egun, baliabide mekanikoen laguntzaz, sekzio koniko hauek errepikatuz, azalera, forma eta kurba perfektuak lortzen dira.
Plano proiektibo erreala
[aldatu | aldatu iturburu kodea]Plano euklidearrean sekzio konikoek antzeko propietate batzuk betetzen dituzte, hori gertatzearen arrazoia hobeto ulertzen da konikoak geometria handiago baten perspektibatik ikustean. Plano euklidearra plano proiektibo errealean txertatu daiteke eta konikoak geometria horretako objektuak kontsideratu daitezke. Hori egiteko modu bat da koordenatu homogeneoak erabiltzea eta konikoa hiru aldagaietako ekuazio koadratiko irreduzible bat betetzen duten puntuen multzo gisa adieraztea. Zehazki, ekuazio koadratiko baten erroen multzoari koadrika deritzo, eta espazio proiektibo bidimentsional batean irreduzibleak diren koadrikei koniko deritze.
Infinituko ebakidura
[aldatu | aldatu iturburu kodea]Plano proiektibo errealean koniko ez-endekatu guztiak baliokideak dira, hori dela eta geometria proiektiboan konika bakarra kontsideratzen da, motarik zehaztu gabe. Hau da, transformazio proiektibo bat existitzen da zeinak koniko mota bati beste koniko mota bat esleitzen dion.[9]
Koniko motak, plano proiektiboko konikoak infinituko zuzenarekin duen ebakiduraren arabera sailkatzen dira. Espazio afinean elipse bat da infinituko zuzenak ez badu konikoa ebakitzen; parabola bat infinituko zuzenak konikoa ebakitzen badu puntu bikoitz batean (ebakidura erpina litzateke); eta hiperbola infinituko zuzenak konikoa asintotei dagokien bi puntutan ebakitzen badu.[10]
Koordenatu homogeneoak
[aldatu | aldatu iturburu kodea]Koordenatu homogeneoetan sekzio koniko bat ondoko eran adieraz daiteke:
Edo modu baliokidean, notazio matriziala erabiliz:
3x3 dimentsiotako matrize horri sekzio konikoaren matrizea deritzo.
Egile batzuek nahiago dute ekuazio homogeneo orokorra honela idatzi:
modu honetan sekzio konikoaren matrizearen adierazpena sinpleagoa delako, [11]
Sekzio konikoaren matrizearen determinantea nulua bada, sekzio konikoa endekatua da.
Ekuazioaren sei koefizienteak konstante ez-nulu batengatik biderkatzean ekuazioaren erroak berdinak izaten jarraitzen dutenez, konikoak moduan adieraz daitezke bost dimentsiotako espazio proiektiboko puntu gisa.
Plano konplexua
[aldatu | aldatu iturburu kodea]plano konplexuan, elipseak eta hiperbolak ez dira desberdintzen; hiperbola bat ardatz irudikaria duen elipse bat izan daiteke. Adibidez, ekuazioak elipse bat definitzen du plano errealean. Ekuazio horretan biraketa irudikari bat egiten badugu, aldagai aldaketa aplikatuz, ekuazioa lortuko genuke. Ekuazio horrek bi ekuazio koniko deskriba ditzake: elipse/hiperbola edo parabola.
plano proiektiboan, berriz, koniko ez-endekatuak ezin dira bereizi haien artean; transformazio lineal bat erabilita ekuazio batetik bestea lor genezake.
Froga daiteke, -n dauden edozein bi sekzio konikok lau puntu berdin dituztela; eta ondorioz, gutxienez ebaki-puntu bat eta gehienez lau izango dituzte. Ebaki-puntuen aukerak hurrengoak dira anizkoiztasunaren arabera :
- Lau puntu singular.
- Bi puntu singular eta anizkoiztasun bikoitzeko bat.
- Anizkoiztasun bikoitzeko bi puntu.
- Puntu singular bat eta anizkoiztasun hirukoitzeko puntu bat.
- Anizkoiztasun laukoitzeko puntu bat. [12]
Ebaki-puntu baten anizkoiztasuna > 1 bada, bi kurbei kurba ukitzaile deritze. Gutxienez anizkoiztasuna hiru duen ebaki-puntu bat badago, bi kurbak oskulatzaileak direla esaten da. Anizkoiztasun laukoitza duen ebaki-puntu bat eta bakarra badago, bi kurbak super-oskulatzaileak dira.
Gainera, zuzen bakoitzak sekzio koniko bakoitza bi aldiz ebakitzen du. Ebaki-puntua bikoitza bada, zuzen horri ukitzaile deritzo. Ebakitzen duen zuzena infinitura hedatzean, sekzio koniko bakoitzak bi puntu ditu infinituan. Bi puntu horiek errealak badira hiperbola bat dugu; irudikari konjugatuak badira elipse bat; eta puntu bikoitza badugu parabola. Ohartzekoa da, elipsearen kasuan puntu horiek eta badira, sekzio konikoa zirkulu bat dela.
Erreferentziak
[aldatu | aldatu iturburu kodea]- ↑ Veblen, Oswald; Young, John Wesley. (1908-10). «A Set of Assumptions for Projective Geometry» American Journal of Mathematics 30 (4): 347. doi:. ISSN 0002-9327. (Noiz kontsultatua: 2019-11-15).
- ↑ «From Plato to Plutarch» Philosopher-Kings of Antiquity (Continuum) ISBN 978-0-8264-3475-3. (Noiz kontsultatua: 2019-12-04).
- ↑ «The value of nursing» Nursing Standard 18 (18): 17–17. 2004-01-14 doi:. ISSN 0029-6570. (Noiz kontsultatua: 2019-12-04).
- ↑ Taharlev, Linda.. (1997-1998). Finishing touches : for 12th grade 4 points. Eric Cohen Books ISBN 965-368-181-8. PMC 234190357. (Noiz kontsultatua: 2019-12-04).
- ↑ Sarton, George. (1928-03). «The Thirteen Books of Euclid's Elements. Thomas L. Heath , Heiberg» Isis 10 (1): 60–62. doi:. ISSN 0021-1753. (Noiz kontsultatua: 2019-12-04).
- ↑ Stillwell, John.. (2010). Mathematics and its history. (3rd ed. argitaraldia) Springer ISBN 978-1-4419-6053-5. PMC 663096669. (Noiz kontsultatua: 2019-12-04).
- ↑ a b «JOHN WILEY & SONS, Inc.» Analytical Chemistry 40 (2): 113A–113A. 1968-02 doi:. ISSN 0003-2700. (Noiz kontsultatua: 2019-12-04).
- ↑ Vieira, Aldo Freitas. Ensino de cálculo diferencial e integral: das técnicas ao humans-with-media. Universidade de Sao Paulo Sistema Integrado de Bibliotecas - SIBiUSP (Noiz kontsultatua: 2019-12-04).
- ↑ Guyot, B.. (2008-01). «Contre la médicalisation de la ménopause avec le THM» Gynécologie Obstétrique & Fertilité 36 (1): 104–109. doi:. ISSN 1297-9589. (Noiz kontsultatua: 2019-12-04).
- ↑ Artzy, Michal. (2015-06-29). «¿Qué hay en un nombre? –Akko-Ptolemais–´Akka-Acre» Complutum 26 (1) doi:. ISSN 1988-2327. (Noiz kontsultatua: 2019-12-04).
- ↑ BLISS, SUZANNE; FERNÁNDEZ, JORDI. (2011-12). «DOES THE SUPERVENIENCE ARGUMENT GENERALIZE?» The Southern Journal of Philosophy 49 (4): 321–346. doi:. ISSN 0038-4283. (Noiz kontsultatua: 2019-12-04).
- ↑ (Ingelesez) Wilczynski, E. J.. (1916-04-01). «Some remarks on the historical development and the future prospects of the differential geometry of plane curves» Bulletin of the American Mathematical Society 22 (7): 317–330. doi:. ISSN 0002-9904. (Noiz kontsultatua: 2019-12-04).

































