Gorputz beltzaren erradiazio

Gorputz beltzaren erradiazioa edozein objektu berok igorritako erradiazio elektromagnetikoari deritzo. Gorputz beltz, idealizatutako gorputz opako eta ez islatzaile bati esaten zaio. Uhin-luzeren espektro espezifikoa du, gorputzaren tenperaturaren menpeko intentsitatearekiko alderantzizko proportzionala dena non kalkulu eta teoriagatik uniformea eta konstantea dela suposatzen den[1][2][3][4]. Objektu arrunt askok berez igorritako erradiazio termikoa, gorputz beltzaren erradiazio gisa hurbil daiteke. Oreka termikoan dagoen guztiz isolatutako itxiturak gorputz beltzaren erradiazioa igortzen du eta horman egindako zirrikitu batetik zehar igorriko da, badin eta egindako zuloak orekan eragindako efektua arbuiagarritzat har badaiteke.
Gela ilun batean giro tenperaturan dagoen gorputza, beltz agertzen da igortzen duen energia gehiena espektro infragorrian dagoelako eta gizakiaren begiak ezin duelako hauteman. Giza begiak tarte ikuskorraren azpitik dauden argi-uhinak ikusi ezin dituenez, tenperatura ikusgai baxuenean gorputz beltza gris ikusten da, nahiz eta, haren espektro fisikoaren maximoa eremu infragorrian kokatzen den[5]. Funtsean, giza begiak argi maila baxuetan ez du kolorerik ikusten, baina, objektua apur bat berotzen denean gorri kolorez agertzen da eta tenperatura areagotu ahala gorri distiratsua, laranja, hori, zuri eta urdin-zurian bihurtzen da.
Planeta eta izarrak haien inguruarekin oreka termikoan egon ez arren eta gorputz beltz perfektuak ez izan arren, haiek igorritako energiaren lehen hurbilketa gisa gorputz beltzaren erradiazioa hartzen da[6]. Zulo beltzak gorputz beltz ia perfektuak dira, bertan erortzen den erradiazio guztia xurgatzen dutelako. Zulo beltzek gorputz beltzaren erradiazioa igortzen dutela proposatua izan da, Hawking-en erradiazioa deiturikoa, non tenperatura zulo beltzaren masaren araberako den [7].
Kontextu historikoa
[aldatu | aldatu iturburu kodea]Balfour Stewart
[aldatu | aldatu iturburu kodea]1858. urtean, Balfour Stewartek hainbat substantzien xafla leunduen erradiazio termikoaren emisio eta xurgatze ahalmenen inguruko esperimentuak deskribatu zituen, tenperatura berean gainazalen beltzen ahalmenekin alderatuta[8].Stewart-ek azalera beltzak aukeratu zituen haren erreferentzia gisa lehenagoko zenbait aurkikuntza esperimental zirela eta, batez ere Pierre Prevost eta John Leslie-renak. Honela idatzi zuen: "Gainazal beltzak, gainean erortzen diren izpi guztiak xurgatzen ditu eta, beraz, ahalik eta xurgatze ahalmen handiena duenak, ahalik eta erradiazio ahalmen handiena izango du".
Stewartek ez zuen adierazi bere aldarrikapenak printzipio orokor abstraktu bat aurresuposatzen zuela: idealki teorian edo benetan errealitatean, gorputz edo gainazalak non ahalik eta xurgatzeko ahalmen unibertsal handiena eta berdina duten, baita irradiatzeko potentzia ere, uhin-luzera eta oreka-tenperatura bakoitzerako existitzen direla.
Stewartek igorritako potentzia neurtu zuen mikroskopioarekin irakurritako termopilarekin eta galbanometro sentikorrarekin. Erradiazio termiko selektiboak kezkatzen zuen, eta erradiazio-kalitate desberdinak irradiatu eta xurgatzen zituzten substantzien plakekin ikertu zuen. Esperimentuak islatu eta errefrakta zitezkeen izpien inguruan eztabaidatu zituen eta Stokes-Helmholtz elkarrekikotasun printzipioa betetzen zuten (horretarako eponimorik erabili ez zuen arren). Artikulu honetan ez zuen aipatu izpien nolakotasunak haien uhin-luzeren arabera deskriba zitezkeenik, eta ez zituen espektroki ebazteko aparatuak erabili ere, hala nola prismak edo difrakzio-sareak.
Bere lana kuantitatiboa zen muga horien barruan. Neurketak giro-tenperaturan egin zituen, eta azkar, berak esperimentuetan erabilitako gorputzak oreka termikotik gertu zeuden egoeran harrapatzeko, irakiten ari zen urarekin orekara berotuz. Bere neurketek baieztatu zuten oreka termikoan igorpen eta xurgapen selektibo berdintasunaren printzipioa errespetatzen dutela modu selektiboan xurgatzen eta igortzen duten substantziek.
Stewartek, eskaini zuen hautatutako erradiazio termiko bakoitzerako hala beharko lukeela frogatzen zuen azalpen teoriko bat, baina, egindako kalkulu matematikoak ez ziren beharko lukeeten bezain zorrotzak baliozkotzak jotzeko[9]. Artikulu honetan ez zuen termodinamikaren inguruko aipamenik egin, nahiz eta energia zinetikoaren kontserbazioa aipatu zuen. Bere neurketek hurrengoa inplikatzen zutela proposatu zuen: erradiazioa propagatzen den materialaren sakonera ezberdinetan dauden partikulek xurgatu eta igortzen dute. Helmholtzen elkarrekikotasun printzipioa aplikatu zuen materialaren interfaze prozesuak barneko materialeko prozesuetatik bereizteko. Ez zituen erabateko gainazal beltz eginezinak postulatzen.
Bere esperimentuek hurrengo ondorioztatu zuten. Oreka termikoan dagoen barrunbe batek edozein zatitatik erradiatutako beroa eta material beltzez osatutako forma eta posizio bereko gainazalak igorritakoa berdinak dira, barrunbea edozein materialekoa izanik ere. Ez zuen esplizituki esan erreferentzia gisa erabiltzen zituen material beltzez estalitako gorputzek tenperaturaren araberako emisio espektraleko funtzio arrunta izan behar zutela.
Gustav Kirchhoff
[aldatu | aldatu iturburu kodea]1859an, Stewarten lanaren berririk izan gabe, Gustav Robert Kirchhoffek espektroki ebaztutako xurgatze-lerroen eta argi ikusgaiaren igorpenaren uhin-luzeren kointzidentziaren berri eman zuen. Halaber, fisika termikoaren onurarako, ikusi zuen lerro distiratsuak edo lerro ilunak, igorlearen eta xurgatzailearen arteko tenperatura diferentziaren araberakoak zirela[10].
Jarraian, Kirchhoff-ek itxitura opako edo barrunbe batean oreka tenperaturan dauden bero erradiazioa igortzen eta xurgatzen duten zenbait gorputz aztertzeari ekin zion.
Hemen Kirchhoff-ek erabili ez zuen notazioa erabiliko da. igorle potentziak dimentsiodun kantitate bat adierazten du: indizeko tenperaturan dagoen gorputzak igorritako erradiazio osoa. Gorputz horren erabateko xurgapen erlazioa dimentsio gabea da, barrunbean tenperaturan xurgatutako erradiazioen eta proportzioaren arteko erlazioa. (Balfour Stewartenarekin alderatuta, Kirchhoffen xurgapen-erlazioaren definizioak ez zuen kolore beltzezko gainazalik aipatzen erradiazio erasotzailearen iturri gisa).
Beraz, erlazioa Igorpen-potentziaren eta xurgapenaren arteko erlazioa dimentsiduna da, igorpen-potentziaren dimentsioekin, -k ez baitu dimentsiorik. Bestalde, gorputzaren uhin-luzeraren igorpen espezifikoa tenperaturan eta uhin-luzera xurgapen espezifikoaren erlazioa adierazten da. Berriro ere, igorpen-potentziaren eta xurgapenaren arteko erlazioaren erlazioa neurri dimentsioduna da, igorpen-potentziaren dimentsioekin.
1859an egindako bigarren txosten batean, Kirchhoffek printzipio edo lege orokor berri bat iragarri zuen eta horretarako froga teoriko eta matematikoak eskaini zituen, nahiz eta ez zuen erradiazioaren potentzien neurketa kuantitatiborik eskaini [11]. Haren froga teorikoa hainbat idazleren artean baliogabetzat joa izan da [9][12]. Hala ere, bere printzipioak iraun du: uhin-luzera bereko bero-izpientzat, tenperatura jakin batean orekan, uhin-luzera espezifikoak igortzearen eta xurgapenaren arteko erlazioak balio komun bera du uhin-luzera horretan igortzen eta xurgatzen duten gorputz guztientzat. Matematikoki legeak dio uhin luzera erlazio espezifikoak balio bera duela gorputz guztientzat, hau da, i indizearen balio guztientzat.
1860an, Stewartek burututako lanaren berririk izan gabe, Kirchhoffek adierazi zuen orekako gorputz batek, igorri eta xurgatzen duen bero erradiazio osoarentzako, erlazioak, indizearen balio bakoitzerako balio bera duela [13]. Berriro ere, potentzia erradiaktiboen neurketarik edo beste datu esperimentalik egin gabe, Kirchhoff-ek uhin-luzera erlazio espezifikoaren balioaren unibertsaltasunaren printzipio berriaren froga teorikoa eskaini zuen. Oraingoan ere, zenbait matematikariek froga teorikoa berri hau baliogabetzat jo izan dute [9][12].
Honela idatz daiteke Kirchhoffen erradiazio termikoaren legea: Oreka termodinamikoan erradiazioa igortzen eta xurgatzen duen edozein tenperaturan, uhin-luzera bakoitzerako, igorpen-potentziaren eta xurgatze-ahalmenaren arteko erlazioak balio unibertsala du, berezkoa gorputz beltz perfektuetan. Hemen bidez irudikatzen dugun igorpen ahalmena da. (Guk deritzoguna, Kirchhoffen jatorrizko idazkeran ikurraz adierazten zen) [13][14][15][16][17][18]
Helge Kraghen arabera, "teoria kuantikoak erradiazio termikoaren azterketari zor dio jatorria, bereziki Robert Kirchhoffek 1859-1860 urteetan lehen definitu zuen gorputz beltzaren erradiazioari" [19].
Teoria
[aldatu | aldatu iturburu kodea]Teoria klasikoa
[aldatu | aldatu iturburu kodea]Gertaera hau klasikoki azaltzeko, Rayleigh eta Jeans orduko teoriak erabiltzen saiatu ziren. Hurbilketa honetan, gorputz beltza orekan dagoela suposatzen da, non bertako atomo guztiak maiztasunarekin oszilatu dezaketen. Bolumen unitateko eta tarteko oszilazio modo kopurua ondorengoa da:
.
Mekanika estatistikoa erabiliz, osziladore klasiko batek energia izateko probabilitatea denez, ondorengo erlazioa lortzen da:
non Boltzmann-en konstantea eta gorputz beltzaren tenperatura diren. Bestalde, oszilatzailearen energia klasikoki da, anplitudeak edozein balio hartu dezakeelarik, beraz, goiko adierazpenaren proportzionaltasun konstantea horrela lortzen da:
.
Mekanika klasikoan, beraz, osziladore baten energiaren batez bestekoa honako hau da:
.
Ondorioz, gorputz beltzaren barruan, eta tarteko moduen bolumen unitateko energia ondorengoa da:
.
Energia dentsitate hau uhin-luzeraren menpe ere idatzi daiteke, ondorengo erlazioa erabiliz:

,
eta azkenik, energia dentsitate hauetatik, erradiantzia kalkulatu daiteke:
,
.
Azken hau lortu ondoren, ebidentzia esperimentalarekin bat ez datorrela argi dago, izan ere, uhin-luzeraren espresioa hartuta, gertatzen da, hau da, uhin-luzera geroz eta txikiagoa denean, energia -rantz doa, esperimentalki energia hori 0-rantz joan beharko litzatekenean. Honi, hondamendi ultramorea deritzo, eta arazo hau konpontzeak fisika kuantikoari hasiera eman zion.
Planck-en teoria
[aldatu | aldatu iturburu kodea]1900. urtean Max Planck zientzialariak datu experimentalekin bat zetorren teoria aurkitu zuela adierazi zuen. Planck-ek aurkitu zuen gorputz beltzaren erradiazioaren formula deribatu zezakeela batezbesteko energia kalkulatzean solidoan dauden oszi- ladoreek igorritako energia diskretua zela adieraziz. Hori dela eta, ondorioztatu zuen energia osziladorearen frekuentziaren propotzioanala zela eta hurrengo eran adierazi zuen:
non propotzionaltasun konstantea Planck-en konstantea den. Orduan, sistema batean hainbat osziladore egon daitekeenez energia bakoitza duen osziladore kopurua Boltzmannen adierazpenak emango du. Kasu honetan, energiaren espektroa diskretua dela hartu behar da kontuan. Hortaz,
.
Ohartu konstantea normalizatuta egon behar dela probabilitatea normalizatua egon behar delako .Hau da, probabilitate guztien batura 1 izan behar da:
.
Orduan, -garren mailan egoteko probabilitatea hurrengoa izango da,
eta adirazpen honetik batezbesteko energia atera daiteke:
Ondorioz, solidoa orekan dagoenean partikulek eta tartean izango duten batezbesteko energia:
Hemendik, maiztasun bakoitzean dagoen bolumen unitateko osziladorea kopurua kontuan hartzean, gorputz beltzaren energia kalkulatu daiteke
Era berean, uhin-luzeraren funtzioan idatzik daiteke
Adierazpen hauetatik solidoak igorritako erradiantzia neurtzen da
Hau guztia dela eta ondoriozta daiteke igorritako erradiazioa tenperaturaren funtzioa dela. Bestalde, maiztasuna oso txikia edo handia denean igorritako potentzioaren balioa txikia izango da. Uhin-luzeraren funtzioan efektu berbera gertatuko da
Wien-en legea
[aldatu | aldatu iturburu kodea]Erradiantzaren adierapena hartuz,
-ren maximoa bilatuz eta T finkoa hartuz Wien-en legearen adierazpena frogatu daiteke, hau da,
T tenperaturan, igorritako potentzia osoa kalkulatu daiteke Planck-en eredua erabiliz
non T tenperatura den eta Stefan–Boltzmann-en konstantea den eta hurrengo balioa hartzen duen:
Aplikazioak
[aldatu | aldatu iturburu kodea]Giza gorputzaren igorpena
[aldatu | aldatu iturburu kodea]Giza gorputzak energia gehiena argi infragorri moduan igortzen du. Igorritako energia osoa, emititutako eta xurgatutako energien diferentzia da:
Stefan-Boltzmann-en legea aplikatuz,

|

|
| Pertsonaren energiaren zati handi bat argi infragorriaren moduan erradiatzen da. Zenbait material gardenak dira infragorrian, baina argi ikusgaiarekiko opakoak dira, infragorriko irudi honetako (beheako) plastikozko poltsa bezala. Beste material batzuk argi ikusgarrirako gardenak dira, baina opakuak edo islatzaileak infragorrian, gizonaren betaurrekoen iluntasunak nabarmentzen ditu. |
non A eta T gorputzaren gainazal azalera eta tenperatura diren, emisibitatea da eta giro tenperatura.
Heldu baten gainazal azalera osoa gutxi
gorabeherea 2-koa da eta larruazalaren eta arropa gehienaren infragorri ertaineko eta urruneko emisibitatea unitatetik gertu dago, gainazal ez metaliko gehienen moduan [20]. Larruazalaren tenperatura 33 °C [21] ingurukoa da, baina arropak gainazaleko tenperatura 28 °C-ra murrizten du giro-tenperatura 20 °C denean [22]. Horregatik, bero erradiatiboaren galera garbia gutxi gorabehera honako hau da:
Egun batean erradiatutako energia osoa 8 MJ ingurukoa da, edo 2000 kcal (janari kaloria). 40 urteko gizonezko baten metabolismo basala [23] ingurukoa da, hau da, eguneko 1700 kcal baliokidea da, 2 -ko azalera bera suposatuz. Hala ere, heldu sedentarioen batez besteko tasa metabolikoa haien tasa basala baino %50 eta %70 inguru handiagoa da.
Galera termiko garrantzitsuen beste mekanismo batzuk ere badaude, konbekzioa eta lurrunketa barne. Kondukzioa arbuiagarria da, Nusselt zenbakia unitatea baino askoz ere handiago da eta. Izerditze bidezko lurrunketari dagokionez, beharrezkoa da soilik erradiazioa eta konbekzioa egoera egonkorreko tenperatura mantentzeko nahikoa ez direnean (baina hala ere, biriketako lurruntzea ematen da). Konbekzio libreko tasak erradiazio tasak baino zertxobait txikiagoak izan arren, hauekin konparagarriak dira [24]. Horrela, erradiazioak energia termikoaren galeraren bi heren inguru hartzen ditu aire fresko eta geldian. Suposizio askoren gutxi gorabeherako izaera kontuan hartuta, estimazio gordin gisa soilik har daiteke. Inguruneko airearen mugimenduak, konbekzio bortxatu edo lurruntzeak eraginez, erradiazioaren garrantzi erlatiboa murrizten du galera termikoko mekanismo gisa.
Wien-en legea giza gorputzaren igorpenetan aplikatuz, uhin luzera maximoa lortzen da:
Arrazoi honengatik, gizakien azterkuntzarako irudi termikoen gailuak sentikortasunik handiena 7-14 mikrometroko uhin-luzera tartean emango da.
Kosmologia
[aldatu | aldatu iturburu kodea]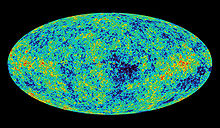
Gaur egun ikusitako hondoko mikrouhin erradiazio kosmikoa naturan inoiz ikusi den gorputz beltzaren erradiaziorik perfektuena da, 2,7 K inguruko tenperatura duena.[25] Unibertsoaren hastapeneko erradiazioaren "argazki" bat da.
Kondepudi eta Prigogineren arabera, oso tenperatura altuetan (1010 K-tik gora; tenperatura horiek oso unibertso goiztiarrean zeuden), non mugimendu termikoak protoiak eta neutroiak bereizten dituen, indar nuklear bortitza egon arren, elektroi-positroi bikoteak agertu eta berez desagertzen dira eta erradiazio elektromagnetikoarekin oreka termikoan daude. Partikula hauek gorputz beltzaren espektroaren zati bat osatzen dute, erradiazio elektromagnetikoaz gain.[26]
Izar baten eta orbitan dagoen planeta baten tenperaturen erlazioa
[aldatu | aldatu iturburu kodea]Gorputz beltza izar bat orbitatzen dagoen planeta baten tenperatura estimatzeko erabili daiteke.

Planeta baten tenperatura zenbait faktoreen menpe dago, hala nola:
- Izarraren erradiazioa.
- Planteak igorritako erradiazioa.
- Albedo efektuak sortzen duen planetak eragindako argiaren islapena.
- Atmosfera duten planeten berotegi efektua.
- Planetak berak sortutako barne energia.
Erlazioa lortzeko eguzkiaren tenperatura kontsideratuz Steffan-Boltzmannen legea erabiltzean igorritako potentzia osoa:
non Steffan-Boltzmannen konstantea eguzkiaren tenperatura eta eguzkiaren erradioa diren.
Eguzkiak potentzia leku guztietara igortzen duenez planetek frakzio oso txiki bat jasotzen dute. Orduan, planetek jasotako potentzia

non planetaren erradioa eta eguzkia eta planetaren arteko distantzia diren.
Tenperatura altuen eraginez, Eguzkiak igorritako espektro elektromagnetiko ultramore edo ikusgarrian kokatzen dira. Frekuentzia hauetan, planetak frakzio bat islatuko du non albedo edo islapen konstantea den. Orduan, planetak xurgatzen duen eguzkiaren frakzioa izango da. Hortaz, xurgatutako potentzia:
Planetak bakarrik sekzio zirkularrean xurgatzen duen arren direkzio guztietan igortzen du. Orduan, Steffan-Boltzmannen legea erabiliz planeta gorputz-beltz bezala hartuta:
non planetaren tenperatua den. Planetaren benetako tenperatura nahiko desber- dina izango da atmosfera eta gainazala kontuan hartzean. Atmosfera eta berotegi efektua arbuiatuz planetak infragorriaren espektroan igorriko du. Frekuentzia honetan, -ko erradiazioa igortzen du non gorputz beltzak igorritako batez-besteko emisibitatea den. Ondorioz, planetak igorrtiako potentzia:
Ekuazioak ordezkatuz planetaren tenperatra lortu daiteke.
Erreferentziak
[aldatu | aldatu iturburu kodea]- ↑ (Loudon 2000), Chapter 1.
- ↑ (Mandel & Wolf 1995), Chapter 13.
- ↑ (Kondepudi & Prigogine 1998), Chapter 11
- ↑ (Landsberg 1990), Chapter 13.
- ↑ Partington, J.R. (1949), p. 466.
- ↑ Ian Morison (2008). Introduction to Astronomy and Cosmology. J Wiley & Sons. p.48. ISBN 978-0-470-03333-3.
- ↑ Alessandro Fabbri; José Navarro-Salas (2005). "Chapter 1: Introduction". Modeling black hole evaporation. Imperial College Press. ISBN1-86094-527-9.
- ↑ (Stewart 1858)
- ↑ a b c (Siegel 1976)
- ↑ (Kirchhoff 1860a)
- ↑ (Kirchhoff 1860b)
- ↑ a b (Schirrmacher 2001)
- ↑ a b (Kirchhoff 1860c)
- ↑ (Chandrasekhar 1950, 8 orr. )
- ↑ (Milne 1930, 80 orr. )
- ↑ (Rybicki & Lightman 1979, 16–17 orr. )
- ↑ (Mihalas & Weibel-Mihalas 1984, 328 orr. )
- ↑ (Goody & Yung 1989, 27–28 orr. )
- ↑ (Kragh 1999, 58 orr. )
- ↑ Infrared Services. "Emissivity Values for Common Materials". Retrieved 2007-06-24.
- ↑ Farzana, Abanty (2001). "Temperature of a Healthy Human (Skin Temperature)". The Physics Factbook. Retrieved 2007-06-24.
- ↑ Lee, B. "Theoretical Prediction and Measurement of the Fabric Surface Apparent Temperature in a Simulated Man/Fabric/Environment System" (PDF). Archived from the original (PDF) on 2006-09-02. Retrieved 2007-06-24.
- ↑ Harris J, Benedict F; Benedict (1918). "A Biometric Study of Human Basal Metabolism".
- ↑ DrPhysics.com. "Heat Transfer and the Human Body". Retrieved 2007-06-24.
- ↑ Bibcode: 1999dpf..conf.....W..
- ↑ (Kondepudi & Prigogine 1998, 227–228 orr. ); also Section 11.6, pages 294–296.





































































