Klotoido

La spiralo de Eŭlero kun ĝiaj du branĉoj. La kurbo konverĝas al du punktoj laŭ ke t alproksimiĝas al pozitiva aŭ negativa infinito.

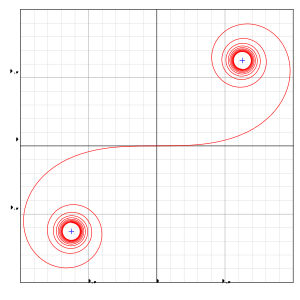
Klotoido, ankaŭ nomata Eŭlera spiralo kaj Spiralo de Cornu, estas ebena kurbo, kies kurbeco varias proporcie al la distanco mezurita laŭ la kurbo.

La ekvacioj de la klotoido unue estis papere dokumentitaj en 1694 fare de la svisa matematikisto Jakob Bernoulli. Tamen, li nek desegnis ĝin nek kalkulis ĝin nombre. Tio estis farita fare de la svisa fizikisto Leonhard Euler en 1743, kiam li retrovis la ekvaciojn dum studado de spirale volvitaj risortoj. Tamen, li ne sukcesis pri determini la limesojn finpunktojn ĝis 1781. En 1874, la ekvacioj denove estis sendepende malkovritaj kaj ekzamenitaj fare de la franca fizikisto Alfred Cornu en difraktokalkuloj. En anglosaksa literaturo, ĝi estas tial kutime referita kiel la spiralo de Euler (Cornu).

Matematikaj superrigardoj de la klotoido

Proprecoj

Ekvacio

Laŭ sia difino klotoido esprimiĝas matematike per la jena formulo: :

$\kappa ={\frac {1}{R}}={\frac {1}{k^{2}}}\cdot l$ (kun $k^{2}>0$),

kie :

$\kappa$ estas la kurbeco kaj $R$ la radiuso de la kurbecocirklo ;

$l$ estas la orientita distanco (pozitiva aŭ negativa laŭ la direkto) sur la kurbo ;

$k$ estas koeficiento (dimensio de longo).

Se l estas pozitiva la kurbeco estas pozitiva, se l estas negativa la kurbeco estas negativa, kaj la origino estas trafleksa punkto. Sekvas ankaŭ ke ${\frac {\mathrm {d} \kappa }{\mathrm {d} l}}={\frac {1}{k^{2}}}=\mathrm {konstanto} \,$, t.e. ke la vario de la kurbeco estas konstanta por ĉiuj punktoj de la kurbo.

Pri ĉiuj punktoj de la kurbo la angulo de la tanĝanto dependas de la distanco el la origino laŭ la formulo $\varphi ={\frac {1}{2}}l^{2}\cdot k^{2}$  ; notu ke la dua derivaĵo laŭ $l$ de tiu angulo estas ankaŭ konstanta, pro la difino de kurbeco.

Unuoklotoido kaj ĝeneraligo

La koeficiento ${\frac {1}{k^{2}}}$ estas pozitiva skalkoeficiento, kiu alĝustigas la grandecon de la klotoido sen modifo de ĝia formo. Do ni ne reduktas la ĝeneralecon de la problemo per postulado ke la "unuoklotoido" estas ebena kurbo tia ke:

• $k=1$ ;
• la origino de la kurbo estas la origino de koordinatoj ;
• la deklivo ĉe la origino estas nula.

Tial la koordinatoj de iu ajn klotoido estas deduktitaj de la "unuoklotoido" per la kombinaĵo de homotetio kun parametro m kaj rotacio de angulo θ kaj translacio de valoro ${\binom {x_{0}}{y_{0}}}$. Tio estas ke se la koordinatoj de la "unuoklotoido" estas ${\binom {X}{Y}}$, la koordinatoj de iu ajn klotoido deduktatas per :

${\binom {x}{y}}=m{\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}{\binom {X}{Y}}+{\binom {x_{0}}{y_{0}}}$.

Por facileco de kalkulado ofte konsideritas la sekvanta formulado: $\,\kappa ={\frac {1}{R}}={\frac {2}{a^{2}}}\cdot l$.

Proprecoj de la unuoklotoido

Ekvacio

La ekvacio estas sendependa de koordinatsistemo :

$R\cdot l=1\,$ aŭ

$l=\kappa \,$ .

Tiu difino ne estas tutmonde adoptata. Anglalingvanoj konsideras la norman Eŭleran spiralon (normalized Euler spiral), kaj adoptas la ekvacion

$\,\,2R\cdot l=1\,$; estas la difinon adoptotan suben.

Parametra formulado

Eblas difini parametre la Eŭleran spiralon per la sekvantaj ekvacioj

$\left\{{\begin{matrix}x(t)&=&\int _{0}^{t}\cos {u^{2}}\,du\\y(t)&=&\int _{0}^{t}\sin {u^{2}}\,du\end{matrix}}\right.$

kie t estas la parametro, u variablo de kaj la integraloj estas la integraloj de Fresnel.

Ĝeneraligo

Ĉiam pri $2R\cdot t=1\,$ : la ĉi-supraj parametraj ekvavioj ekvivalentas al unu nura ekvacio formulata en la kompleksa ebeno :

$p(t)=\int _{0}^{t}e^{iu^{2}}\,du$

kun:
Longo de la kurbo ĝis la loka punkto : $l=t$
Angulo de la tanĝanto ĉe tiu punkto : $\varphi =t^{2}$
Loka radiuso de kurbeco : $R={\frac {1}{2t}}$

Limesaj punktoj

La norma Eŭlera spiralo konverĝas al limesaj punktoj kiam l alproksimiĝas al infinito (vidu bildon):

$x^{p}=\lim _{L\to \infty }\int _{0}^{L}\cos \left(s^{2}\right)\,ds={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx 0.6267\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y^{p}=\lim _{L\to \infty }\int _{0}^{L}\sin \left(s^{2}\right)\,ds={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx 0.6267$;

$x^{n}=\lim _{L\to -\infty }\int _{0}^{L}\cos \left(s^{2}\right)\,ds=-{\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx -0.6267\,,\,\,\,\,y^{n}=\lim _{L\to -\infty }\int _{0}^{L}\sin \left(s^{2}\right)\,ds=-{\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx -0.6267$.

Utileco kaj aplikoj

La kurbo, kiu kunigas la rektan linion al la cirklo estas la klotoido. Ĝi estas karakterizita per konstanta kaj eta variaĵo (= ${\frac {1}{k^{2}}}$) de sia kurbeco el la rekto
($\kappa =0$) al la cirklo kun donita kurbeco ($\kappa ={\frac {1}{r}}$).

Klotoidoj havas aplikojn en optiko por difraktokomputadoj. Ili ankaŭ estas vaste uzitaj en fervoja kaj aŭtovoja inĝenierarto por dezajni transirkurbojn inter rektaj kaj kurbaj sekcioj de fervojoj aŭ vojoj. Simila aplikiĝo ankaŭ estas trovita en fotonaj integraj cirkvitoj.

Desegnado de vojaj kaj fervojaj itineroj

La problemo unue ekestis en la fervoja domajno, kiam la rapideco de trajnoj kreskis. Studite de la usona inĝeniero Arthur Talbot (dum fino de la 19-a jarcento), li trovis ke ligo de la rekta linio kaj la arko de cirklo per segmento de klotoido ebligas forigi flankajn ŝokojn kaj permesi moderan linearan pliiĝon de la centrifuga forto.

Sur aŭtovojo, la trajektorio sekvata de aŭtomobilo veturanta kun konstanta rapido kiam la aŭtomobilisto turnas la stirilon je konstanta rapido (t.e. la modifo de la stira angulo estas konstanta) estas klotoido.

Ne estas analitika solvo de la ekvacioj de klotoido, necesas procedi per cifereca integriĝo. Estas tabeloj, kiuj donas la parojn $x(l)$ kaj $y(l)$ por diversaj valoroj de $k^{2}$ por interkonekti rekton kun cirklon aŭ rekton kun alia rekto.

Noto: estas ankaŭ necese kalkuli la deklivon (kiu varias kun $l$, ĉar la radiusa akcelo pliiĝas kun $l$) de la trafikvojo tiel ke la reago de la veturilo estu kiel eble plej orta al la vojo.

Telferoj

Sammaniere, la "ŝuoj" muntitaj sur la pilonoj de telferoj, kaj kiuj subtenas la portantkablon, adoptas klotoidan formon (per sukcedo de du segmentoj de klotoido) por cirkuligi la kabinon je maksimuma rapido sur la pilonoj sen ĝeni la pasaĝerojn.

Eksteraj ligiloj

• Spiralo de Cornu (france). Enciklopedio pri rimarkindaj matematikaj formoj.