Gamma (eclipse)
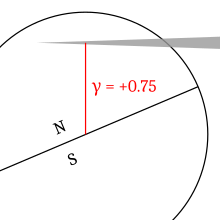
Gamma (denoted as γ) of an eclipse describes how centrally the shadow of the Moon or Earth strikes the other body. This distance, measured at the moment when the axis of the shadow cone passes closest to the center of the Earth or Moon, is stated as a fraction of the equatorial radius of the earth (6378.137 km).[1]
Sign
[edit]The sign of gamma defines, for a solar eclipse, if the axis of the shadow passes north or south of the center of the Earth; a positive value means north. The Earth is defined as that half which is exposed to the Sun (this changes with the seasons and is not related directly to the Earth's poles or equator; thus, the Earth's center is wherever the Sun is directly overhead).
For a lunar eclipse, it defines whether the axis of the Earth's shadow passes north or south of the Moon; a positive value means south.
Gamma changes monotonically throughout any single saros series. The change in gamma is larger when Earth is near its aphelion (June to July) than when it is near perihelion (December to January). For odd numbered series (ascending node for solar eclipses and descending node for lunar eclipses), gamma decreases for solar eclipses and gamma increases for lunar eclipses, while for even numbered series (descending node for solar eclipses and ascending node for lunar eclipses), gamma increases for solar eclipses and gamma decreases for lunar eclipses. This simple rule describes the current behavior of gamma, but this has not always been the case. The eccentricity of Earth's orbit is presently 0.0167, and is slowly decreasing. It was 0.0181 in the year −2000 and will be 0.0163 in +3000. In the past, when the eccentricity was larger, there were saros series in which the trend in gamma reversed for one or more saros cycles before resuming its original direction, most noticeable in series 0 where the temporary reversal caused a series of 3 partial eclipses to occur after 6 umbral eclipses had already occurred, before resuming with a series of 45 annular eclipses, due to gamma decreasing from −0.9882 in member 14 to −1.0050 in member 19 before resuming the positive trend.[2] These instances occur near perihelion when the Sun's apparent motion is highest and may, in fact, overtake the eastward shift of the node. The resulting effect is a relative shift west of the node after one saros cycle instead of the usual eastward shift. Consequently, gamma reverses direction.
Gamma for solar eclipses
[edit]Gamma at a solar eclipse is related to the minimal value of the elongation of the moon (its angular distance from the sun) as it would appear to a hypothetical observer at the centre of the earth, and to the distance of the moon from the earth. Gamma is the sine of the elongation times the lunar distance divided by the equatorial radius of the earth. Since the equatorial radius of the earth is 6378 km and the distance to the moon at new moon varies between about 356,353 and 406,720 km (see lunar distance), gamma for an elongation of 1° is between 0.975 and 1.113.
The absolute value of gamma (denoted as |γ|) distinguishes between different types of solar eclipses that are seen on Earth.[3]
If the Earth were a perfect sphere, the maximum value of |γ| that a central eclipse[α] could have would be 1.0. However, due to the oblateness of the Earth (which causes the length of the Earth's polar radius to be about 20 km shorter than the equatorial radius), the maximum value of |γ| that a central eclipse could have is 0.9972.[4]
| |γ| | Type of eclipse | Notes |
|---|---|---|
| 0 | Central[α] | The axis of the shadow cone is exactly between the northern and southern halves of the sunlit side of the Earth |
| between 0 and 0.9677826 | Central[α] | |
| between 0.9677826 and 0.9972 | Central[α] (one limit) | One edge of the shadow cone misses the Earth |
| between 0.9972 and 1.0266174 | non-central | The axis of the shadow cone misses Earth, but, portions of the umbra or antumbra do intersect the Earth (generally in the polar regions) given the shadow cone's nonzero width. |
| between 1.0266174 and approximately 1.55[β] | Partial | |
| Greater than approximately 1.55[β] | No eclipse |
- ^ a b c d Defined as locations on Earth exist in which the Moon can be seen centered in front of the Sun. The eclipse can either be total or annular depending on the exact distance separating the earth from the moon (total eclipse occurs for shorter distances, annular eclipse occurs for longer distances)
- ^ a b See discussion below.
The exact upper limiting value of |γ| for a partial eclipse depends on the exact distance separating the earth from the moon. It is made of three parts:
- varies between 0.2558 and 0.3018
This gives a range for |γ| of 1.525, when the sun is near and the moon far, to 1.571 in the opposite situation.[5] Note that for a |γ| value of 1.55, a smaller moon (further away) gives a partial eclipse whereas a larger moon (closer to Earth) does not produce an eclipse. Eclipses cannot occur if the elongation (for a hypothetical observer an the centre of the earth or on the surface at the location where the moon is at the zenith) is greater than 1.573° (corresponding to |γ|≈1.534, with both the sun and the moon at their minimum distances), whereas an eclipse will definitely occur if the elongation is below 1.40° (corresponding to |γ|≈1.561, with the sun and moon at their maximum distances).
The Solar eclipse of April 29, 2014, with a gamma of −0.99996, is an example of the special case of a non-central annular eclipse. The axis of the shadow cone barely missed Earth's south pole. Thus, no central line could be specified for the zone of annular visibility.[6]
The next non-central eclipse in 21st century is total solar eclipse of April 9, 2043.
Limiting cases for lunar eclipses on the Moon with respect to Earth's umbral and penumbral shadows
[edit]There are three types of lunar eclipses:
- Penumbral lunar eclipse = The Moon passes through Earth's penumbra, but the Earth's umbra misses the Moon.
- Partial lunar eclipse = The Moon passes through Earth's umbra, but not completely.
- Total lunar eclipse = The Moon passes through Earth's umbra, completely.
We have the following cases:
- If |γ| is 0, the Moon's center passes exactly through the axis of the Earth's umbra.
- If |γ| is lower than 0.2725, this lunar eclipse is central.
- If |γ| is between 0.2725 and 0.48, this lunar eclipse is total.
- If |γ| is between 0.44 and 0.9972, this lunar eclipse is partial with a penumbral magnitude greater than 1.
- If |γ| is between 0.987 and 1.0266174, this lunar eclipse is total penumbral or partial with a penumbral magnitude less than 1.
- If |γ| is between 1.0266174 and approximately 1.55, this lunar eclipse is penumbral with penumbral magnitude less than 1, the Moon traverses only the Earth's penumbra.
- If |γ| exceeds approximately 1.55, the Earth's penumbra misses the Moon completely, and no eclipse occurs. The exact value depends on the distance of the moon and of the sun, exactly as for solar eclipses (see above).
References
[edit]- ^ "Key to catalog of solar eclipses". NASA Eclipse Website. NASA., "Key to catalog of lunar eclipses". NASA Eclipse Website. NASA.
- ^ "NASA - Catalog of Solar Eclipses of Saros 0".
- ^ J. Meeus: Astronomical Algorithms. 2nd ed., Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Chapter 54
- ^ J. Meeus: Mathematical Astronomy Morsels III. Willmann-Bell, Richmond 2004, ISBN 0-943396-81-6, Chapter 6
- ^ See J. Meeus: Mathematical Astronomy, Morsels, Willmann-Bell, 2000, ISBN 0-943396-51-4, Fig. 10.c. and J. Meeus: Mathematical Astronomy, Morsels III, Willmann-Bell, 2004, ISBN 0-943396-81-6, Page 46
- ^ "Path of Annular Solar Eclipse of 2014 Apr 29". eclipse.gsfc.nasa.gov. Retrieved 2024-04-09.










