Quantitative Analysis of the Conservation of the Tertiary Structure of Protein Segments

 

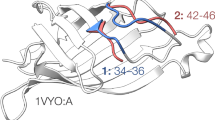
The publication of the crystallographic structure of calmodulin protein has offered an example leading us to believe that it is possible for many protein sequence segments to exhibit multiple 3D structures referred to as multi-structural segments. To this end, this paper presents statistical analysis of uniqueness of the 3D-structure of all possible protein sequence segments stored in the Protein Data Bank (PDB, Jan. of 2003, release 103) that occur at least twice and whose lengths are greater than 10 amino acids (AAs). We refined the set of segments by choosing only those that are not parts of longer segments, which resulted in 9297 segments called a sponge set. By adding 8197 signature segments, which occur uniquely in the PDB, into the sponge set we have generated a benchmark set. Statistical analysis of the sponge set demonstrates that rotating, missing and disarranging operations described in the text, result in the segments becoming multi-structural. It turns out that missing segments do not exhibit a change of shape in the 3D-structure of a multi-structural segment. We use the root mean square distance for unit vector sequence (URMSD) as an improved measure to describe the characteristics of hinge rotations, missing, and disarranging segments. We estimated the rate of occurrence for rotating and disarranging segments in the sponge set and divided it by the number of sequences in the benchmark set which is found to be less than 0.85%. Since two of the structure changing operations concern negligible number of segment and the third one is found not to have impact on the structure, we conclude that the 3D-structure of proteins is conserved statistically for more than 98% of the segments. At the same time, the remaining 2% of the sequences may pose problems for the sequence alignment based structure prediction methods.

Appendix 1

For proving that an absolutely conserved segment must be a conserved segment, we first consider the definition of URMSD. We need to prove the following statement mathematically.

Let

$$ d(\{v_i\},\{w_i\})=\min\nolimits_\phi\left\{{\sqrt{\frac{1}{n} \sum\limits_{i=1}^n {\vert\vert v_i-\phi (w_i)\vert\vert^2}}}\right\} $$

be the URMSD between the two unit vector sequences $\left\{{v_i}\right\}_{i=1}^n$ and $\left\{{w_i}\right\}_{i=1}^n$, and let d _i be the URMSD between the pair of $v_{i+1},\ldots,v_{i+5}$ and $\phi (w_{i+1}),\ldots,\phi (w_{i+5})$.

Then $d(\{v_i\},\{w_i\})\leq \max\{d_i\;\vert \;i=0,1,2,\ldots,n-5\}$ for all $n\geq 10$.

Proof. It is easily followed that

$$\begin{array}{l} \min_\phi \left\{\sqrt{\frac{1}{n}\sum\limits_{i=1}^n {\vert\vert v_i-\phi (w_i)\vert\vert^2}}\right\}\\ \mathop{=}\limits^{y_i =\phi (w_i)}\min_{\{\phi\}} \left\{{\sqrt{\frac{1}{n}\sum\limits_{i=1}^n {\vert\vert v_i-\phi (w_i)\vert\vert^2}}} \right\}\\ =\min_{\{\phi\}} \left\{{\sqrt{\frac{1}{n}\sum\limits_{i=1}^n {\vert \vert v_i\vert\vert^2+\vert\vert\phi (w_i)\vert\vert^2-2(v_i,\phi (w_i))}}}\right\}\\ =\min_{\{\phi\}} \left\{{\sqrt {\frac{1}{n}\sum\limits_{i=1}^n {[2-2(v_i,\phi (w_i))]}}}\right\}\\ =\min_{\{\phi\}} \left\{\sqrt{2-\frac{2}{n}\sum\limits_{i=1}^n {(v_i,\phi (w_i))}}\right\}\\ \end{array}$$

We can regard that $\sum\limits_{i=1}^n (v_i,\phi (w_i))$ as the trace of the correlation matrix R(n), where

$$ R(n,\phi)=\left({\begin{array}{l} (v_1,\phi (w_1))\;(v_1,\phi (w_2 ))\;\ldots\;(v_1,\phi (w_n))\\ (v_2,\phi (w_1))\;(v_2,\phi (w_2 ))\;\ldots\;(v_2,\phi (w_n))\\ \quad\ldots \;\ldots \\ (v_n,\phi (w_1))\;(v_n,\phi (w_2))\;\ldots\;(v_n,\phi (w_n))\\ \end{array}}\right). $$

That is, we have

$$ d(\{v_i\},\{w_i\})=\min\nolimits_{\{\phi\}} \sqrt{\frac{2n-2\times \hbox{trace}(R(n,\phi))}{n}} $$

For a fixed ϕ and every pair of five-unit-vector $v_{i+1}, \ldots ,v_{i+5}$ and $\phi (w_{i+1}),\ldots ,\phi (w_{i+5})$, we have a correlation matrix

$$ R_i (5)=\left({\begin{array}{l} (v_{i+1},\phi (w_{i+1}))\;(v_{i+1},\phi (w_{i+2}))\;\ldots \;(v_{i+1}, \phi (w_{i+5}))\\ (v_{i+2},\phi (w_{i+1}))\;(v_{i+2},\phi (w_{i+2}))\;\ldots \;(v_{i+2}, \phi (w_{i+5}))\\ \quad\ldots \;\ldots .\\ (v_{i+5},\phi (w_{i+1}))\;(v_{i+5},\phi (w_{i+2}))\;\ldots \;(v_{i+5}, \phi (w_{i+5}))\\ \end{array}}\right) $$

Let $d_i =\sqrt{\hbox{trace}(R_i (5)^\prime R_i (5))}$ for $i=0,1,2,\ldots ,n-5$. For convenience, then we may assume $d_0 =\max\{d_i\;\vert \;i=0,1,2,\ldots ,n-5\}$, then

$$ \sqrt {\sum\limits_{j=1}^5 {\sum\limits_{j=1}^5 (v_i,\phi (w_j))^2}} \geq\sqrt{\sum\limits_{j=1}^5 {\sum\limits_{j=1}^5 (v_{i+k},\phi (w_{j+k}))^2}}\hbox{ for all }k\geq 1. $$

Considering the relationship

$$ \begin{array}{l} \sqrt{\hbox{tr}(R(n)^\prime R(n))} =\sqrt{\sum\limits_{j=1}^n \sum\limits_{i=1}^n {(v_i,\phi (w_j))^2}} =\sqrt {\sum\limits_{j=1}^n (\sum\limits_{i=1}^5 (v_i,\phi (w_j))^2+\sum\limits_{i=5}^n (v_i,\phi (w_j))^2)}\\ =\sqrt{\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,\phi (w_j))^2+} \sum\limits_{j=6}^n\sum\limits_{i=1}^5 {(v_i,\phi (w_j))^2+ \sum\limits_{j=1}^5\sum\limits_{i=6}^n {(v_i,\phi (w_j))^2+ \sum\limits_{j=6}^n\sum\limits_{i=6}^n {(v_i,\phi (w_j))^2}}}}\\ \end{array} $$

By ordinary fact of structure of protein: for most AAs, the state at site i is not more frequently correlated to the state at site j if the distance between the two sites is greater than 5 AAs. That is, we may assume that $R(n)^\prime R(n)$ has the following relations mathematically:

• The number of the set $\left\{{k\;\vert \;\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,\phi (w_j))^2 <\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_{i+k},\phi (w_j))^2}}} \right\}$ related to n − 5 is very small.

• The number of the set $\left\{{k\;\vert \;\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,\phi (w_j))^2 <\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,\phi (w_{j+k}))^2}}} \right\}$ is also very small related to n − 5.

• $(v_i,\phi (w_j))^2>(v_{i+k},\phi (w_j))^2$ and $(v_i,\phi (w_j))^2>(v_i,\phi (w_{j+k}))^2$ for all $i,j\leq 5$ and almost all k > 6.

Then let $y_i =\phi (w_i)$, we have

• $\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,y_j)^2 \geq\sum\limits_{j=5}^5 \sum\limits_{i=1}^5 {(v_{i+k},y_j)^2}}$,

• $\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,y_j)^2 \geq\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,y_{j+k})^2}}$

• $\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,y_j)^2 \geq\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_{i+k},y_{j+k})^2}}$

for all k > 6. Without lost the generality, we may assume that $n=0\;(\hbox{mod}5)$, and then we have

$$ \begin{array}{l} \frac{1}{n}\sqrt{\hbox{tr}(R(n)^{\prime}R(n))} =\sqrt{\frac{1}{n^2} \sum\limits_{j=1}^n\sum\limits_{i=1}^n {(v_i,y_j)^2}}\\ =\sqrt{\frac{1}{n^2}\left({\sum\limits_{j=1}^5\sum\limits_{i=1}^5 {(v_i,y_j)^2+}\sum\limits_{j=6}^n\sum\limits_{i=1}^5 {(v_i,y_j)^2+ \sum\limits_{j=1}^5\sum\limits_{i=6}^n {(v_i,y_j)^2+ \sum\limits_{j=6}^n\sum\limits_{i=6}^n {(v_i,y_j)^2}}}}\right)}\\ =\sqrt{\frac{1}{n^2}\left({\frac{n}{5}\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,y_j)^2+}\sum\limits_{j=6}^n\sum\limits_{i=1}^5 {(v_i,y_j)^2+\sum\limits_{j=1}^5\sum\limits_{i=6}^n {(v_i,y_j)^2}}} \right)}\\ \quad \leq\sqrt{\frac{1}{n^2}\left({\frac{n}{5}\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,y_j)^2+} \frac{n-5}{5}\sum\limits_{i=1}^5 {(v_i,y_j)^2+\frac{n-5}{5}\sum\limits_{j=1}^5 {(v_i,y_j)^2}}}\right)}\\ \quad \leq\sqrt{\frac{1}{n^2}\left({\frac{n}{5}\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,y_j)^2+} \frac{n-5}{5}\sum\limits_{i=1}^5 {\sum\limits_{j=1}^5 {(v_i,y_j)^2}}}\right)}\\ =\sqrt{\frac{2n-5}{5n^2}\left({\sum\limits_{j=1}^5\sum\limits_{i=1}^5 {(v_i,y_j)^2}}\right)} <\sqrt {\frac{2}{5n}\left({\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,y_j)^2}} \right)} \mathop{\leq} \limits^{n\geq 10} \frac{1}{5}\sqrt {\hbox{trace}(R(5)^{\prime}R(5)}\\ \end{array} $$

That is, we have proved that

$$ \frac{\sqrt{\sigma_1 (n)^2+\sigma_2 (n)^2+\cdots +\sigma_n(n)^2}} {n}<\frac{\sqrt{\sigma_1 (5)^2+\sigma_2 (5)^2+\cdots +\sigma_5 (5)^2}}{5}\hbox{ if }n\geq 10. $$

where $\sigma_i (j)$ for $j=5,n$ and $i\leq j$, are the singular value of R(5) and R(n) respectively. Replacing R(n) and R(5) by their “squared root”:

$$ R^{\frac{1}{2}}(n)=\left({\begin{array}{l} \sqrt{\vert (v_1,y_1)\vert} \;\sqrt{\vert (v_1,y_2)\vert} \;\ldots.\;\sqrt{\vert (v_1,y_n)\vert}\\ \sqrt{\vert (v_2,y_1)\vert} \;\sqrt{\vert (v_2,y_2)\vert} \;\ldots .\;\sqrt{\vert (v_2,y_n)\vert}\\ \quad\ldots .\;\ldots .\\ \sqrt{\vert (v_n,y_1)\vert} \;\sqrt{\vert (v_n,y_2)\vert} \;\ldots .\;\sqrt{\vert (v_n,y_n)\vert}\\ \end{array}} \right) $$

and with the same argument, we have

$$ \frac{\sigma_1 (n)+\sigma_2 (n)+\cdots +\sigma_n (n)}{n}< \frac{\sigma_1(5)+\sigma_2 (5)+\cdots +\sigma_5 (5)}{5} \quad \hbox{ if }n\geq 10. $$

That is, $\frac{\hbox{trace}(svd\;R(5))}{5}>\frac{\hbox{trace}(svd\;R(n))}{n}$ for $n\geq 10$.

Therefore, the maximal URMD among the all five-unit-vectors is greater than the URMSD for the whole segment. This ends the proof.