Singulární rozklad
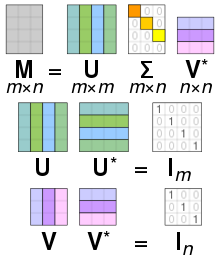
Singulární rozklad (zkratkou SVD podle anglického názvu Singular Value Decomposition) matice je rozklad komplexní nebo reálné matice na maticový součin . Přitom je reálná nebo komplexní unitární matice o rozměrech , je reálná nebo komplexní unitární matice a je matice nulová až na případná nezáporná čísla na hlavní diagonále; čísla na její hlavní diagonále se označují jako singulární hodnoty matice . Hvězdička označuje konjugovanou matici, tedy transponovanou matici komplexně sdružených prvků. Požadujeme-li, jak je obvyklé, aby singulární hodnoty byly seřazeny sestupně, je matice určena jednoznačně, naopak matice a jednoznačné být nemusejí. Singulární rozklad vždy existuje a používá se k řadě teoretických i praktických účelů. Lze ho chápat také jako zobecnění Schurova rozkladu na matice obecného tvaru. Nevýhodou je, že výpočetní náročnost konstrukce singulárního rozkladu roste se třetí mocninou rozměru matic. O vypracování teorie singulárních hodnot se zasloužili matematici Eugenio Beltrami (1873), Camille Jordan (1874), James Joseph Sylvester (1889), Erhard Schmidt (1907), Émile Picard (1910) a Eckart a Young (1936). První algoritmus SVD rozkladu publikovali Gene H. Golub a William Kahan (1965), jeho vylepšenou a dodnes často používanou variantu uveřejnili Golub a Christian Reinsch (1970).
Geometricky existence singulárního rozkladu znamená, že každý lineární operátor mezi reálnými vektorovými prostory konečných dimenzí lze rozložit na rotaci vzorů (matice ), vynásobení (části) rotovaných vektorů nezápornými koeficienty (singulárními hodnotami) a opětnou rotaci (případně rotaci kombinovanou se zrcadlením) v prostoru obrazů (matice ). Anebo můžeme matice a interpretovat jako matice přechodu mezi bázemi a říci, že pro každý lineární operátor mezi reálnými konečněrozměrnými vektorovými prostory lze najít dvojici ortonormálních bází (v prostoru vzorů a v prostoru obrazů) tak, že daný operátor se v těchto bázích zapíše jako matice s nezápornými čísly na hlavní diagonále a nulami všude jinde, tj. i-tou složku vzoru v první bázi násobí i-tou singulární hodnotou, čímž získá i-tou složku zápisu obrazu ve druhé bázi.











