Тиҙлек
| Тиҙлек | |
 | |
| Алдағы | перемещение[d] |
|---|---|
| Тәртип буйынса һуңыраҡ килеүсе | тиҙләнеш |
| Асыусы йәки уйлап табыусы | Пьер Вариньон[d] |
| Үлсәме | |
| Закон йәки теорема формулаһы | [1][2] |
| Обозначение в формуле | , һәм |
| Дәүмәл символы (LaTeX) | [2], , , , һәм |
| Вики-проект | Проект:Математика[d] |
| Рекомендуемая единица измерения | метр в секунду[d][2][3] һәм километр в час[d][4] |
| Скорость | |
| Үлсәнеш |
LT−1 |
|---|---|
| Үлсәү берәмеге | |
| СИ |
м/с |
| СГС |
см/с |
| Примечания | |
|
вектор | |
Тиҙлек (стандарт тамғаланышы , ингл. velocity йәки франц. vitesse һүҙҙәренән) — векторлы физик дәүмәл, ул материаль нөктәнең һайланған иҫәпләү системаһына ҡарата күсеш етеҙлеген һәм хәрәкәт йүнәлешен күрһәтә. Билдәләмә буйынса нөктәнең радиус-векторының ваҡыт буйынса сығарылмаһына тигеҙ. СИ системаһында секундына метрҙарҙа үлсәнә.
Рус телендә ошо уҡ һүҙ менән скаляр дәүмәлде — йәки нөктәнең тиҙлек векторының модулен, йәки алгебраик тиҙлеген, йәғни векторының нөктә траекторияһына тейеүсе проекцияһын атайҙар[5]. Ҡайһы бер башҡа телдәрҙә скаляр тиҙлек өсөн айырым атамалар бар, мәҫәлән ингл. speed, лат. celeritas.
«Тиҙлек» термины фәндә һәм, уны ниндәйҙер дәүмәлдең (мотлаҡ радиус-векторҙың ғына түгел) икенсеһенә бәйле үҙгәреү тиҙлеге (йышыраҡ ваҡытта үҙгәреүе күҙ уңында тотола, ләкин шулай уҡ арауыҡта йәки башҡа) тип аңлап, киң мәғәнәлә лә ҡулланыла. Шулай, мәҫәлән, мөйөш тиҙлеге, температураның үҙгәреү тиҙлеге, химик реакция тиҙлеге, тҡркөм тиҙлеге, берләшеү тиҙлеге һәм башҡалар тураһында һөйләнелә. Математикала «үҙгәреү тиҙлеге» ҡаралған дәүмәлдең сығарылмаһы менән характерлана.
Классик механикала «тиҙлек» төшөнсәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Материаль нөктә осрағы
[үҙгәртергә | сығанаҡты үҙгәртеү]Материаль нөктәнең һәр ваҡыт моментында тиҙлек векторы (моменталь тиҙлек) был нөктәнең ағымдағы торошоноң радиус-векторының ваҡыт буйынса сығарылмаһы түбәндәгесә билдәләнә[6]:
бында — траекторияның ағымдағы нөктәһе аша үткән тейеүсенең берәмек векторы (ул хәрәкәт итеүсе нөктәнең дуға координатаһының үҫеү яғына йүнәлгән), ә — дуға координатаһының ваҡыт буйынса сығарылмаһына тигеҙ булған һәм нөктәнең алгебраик тиҙлеге тип аталған, тиҙлек векторының телгә алынған берәмек вектор йүнәлешенә проекцияһы. Килтерелгән формулаларға ярашлы, нөктәнең тиҙлек векторы һәр ваҡыт тейеүсе буйлап йүнәлгән, ә нөктәнең алгебраик тиҙлеге был векторының модуленән тик тамғаһы менән генә айырылырға мөмкин[7]. Был ваҡытта:
- әгәр дуға координатаһы үҫһә, һәм векторҙары бер йүнәлешле, ә алгебраик тиҙлек ыңғай;
- әгәр дуға координатаһы кәмеһә, һәм векторҙары ҡапма-ҡаршы йүнәлешле, ә алгебраик тиҙлек тиҫкәре.
Нөктәнең -дән алып -ға тиклем ваҡыт аралығында үткән юлы ошолай табыла
- .
Нөктәнең алгебраик тиҙлеге һәр ваҡыт тиҫкәре булмаһа, юл дуға координатаһының -дән алып -ға тиклемге ваҡыт эсендә ҡушымтаһы менән тап килә (әгәр шул уҡ ваҡытта дуға координатаһының иҫәпләү башы хәрәкәт итеүсе нөктәнең башланғыс торошо менән тап килһә, менән тап киләсәк).

Әгәр нөктәнең алгебраик тиҙлеге ваҡыт үтеү менән үҙгәрмәһә (йәки, шул уҡ, тиҙлек модуле даими булһа), нөктәнең хәрәкәте [8] тигеҙ хәрәкәт тип атала (алгебраик тейеүсе тиҙләнеш был ваҡытта тождестволы нулгә тигеҙ).
тип уйлайыҡ. Ул саҡта тигеҙ хәрәкәттә нөктәнең тиҙлеге (алгебраик) үтелгән юлының был юл үтелгән ваҡыт аралығына бүлендегенә тигеҙ була:
Дөйөм осраҡта
- һәм
сағыштырмалары ярашлы рәүештә нөктәнең уртаса тиҙлеген [9] һәм уның урта алгебраик тиҙлеген билдәләйҙәр; әгәр «уртаса тиҙлек» термины менән ҡулланғанда, һәм дәүмәлдәре тураһында (буталмаҫ өсөн) моменталь тиҙлек һымаҡ әйтелә.
Юғарыла индерелгән уртаса тиҙлектең ике төшөнсәһе араһында айырма шунан тоа. Беренсенән, — вектор, ә — скаляр. Икенсенән, был дәүмәлдәр модуле буйынса тап килмәҫкә мөмкиндәр. Шулай, нөктә винт һыҙығы буйлап хәрәкәт итһен ти, һәм үҙенең хәрәкәте ваҡытында бер уратым үтһен; ул саҡта был нөктәнең уртаса тиҙлек модуле винт һыҙығының аҙымының (йәғни уның уратымдары араһындағы алыҫлыҡтың) хәрәкәт ваҡытына бүлендегенә тигеҙ, ә урта алгебраик тиҙлектең модуле — уратым оҙонлоғоноң хәрәкәт ваҡытына бүлендегенә тигеҙ.
Сикле үлсәмле есем осрағы
[үҙгәртергә | сығанаҡты үҙгәртеү]Киңәйтелгән үлсәмле есем өсөн «тиҙлек» төшөнсәһен (есемдең үҙенең, ә уның нөктәләренең береһенең түгел) билдәләп булмай; моменталь-ынтылышлы хәрәкәт осрағы ҡағиҙәнән ситләшеү булып тора. Әгәр бирелгән ваҡыт моментында есемде төҙөүсе бөтә нөктәләрҙең тиҙлектәре тигеҙ булһа, абсолют ҡаты есем моменталь-ынтылышлы хәрәкәт яһай тип әйтәләр[10]; ул саҡта, аңлашылыуынса, есемдең тиҙлеге уның теләһә ниндәй нөктәһенең тиҙлегенә тигеҙ тип иҫәпләп була. Шулай, мәҫәлән, күҙәтеү ҡуласаһы кабинаһының бөтә нөктәләренең тиҙлеге тигеҙ (әлбиттә әгәр кабинаның тирбәлеүҙәрен иҫәпкә алмағанда).
Дөйөм осраҡта ҡаты есемде төҙөүсе бөтә нөктәләрҙең тиҙлектәре үҙ-ара тигеҙ түгел. Шулай, мәҫәлән, шыумайынса тәгәрләп хәрәкәт итеүсе тәгәрмәс өсөн юлға ҡарата нөктәләрҙең тиҙлек модулдәре нулдән алып (юл менән тейеү нөктәһендә) тәгәрмәс үҙәге тиҙлегенең икеләтелгән ҡиммәтенә тиклем (тейеү нөктәһенә диаметраль рәүештә ҡапма-ҡаршы нөктәлә) ҡиммәттәр ҡабул итә. Абсолют ҡаты есем нөктәләренең тиҙлектәре бүленеше Эйлерҙың кинематик формулаһы менән тасуирлана.
Төрлө координаталар системаларында тиҙлектең яҙылышы
[үҙгәртергә | сығанаҡты үҙгәртеү]Декарт координаттар системаһы
[үҙгәртергә | сығанаҡты үҙгәртеү]Тура мөйөшлө декарт координаталар системаһында[11]::
, шуға күрә
Шулай итеп, тиҙлек векторының компоненттары — материаль нөктәнең ярашлы координаталарының үҙгәреү тиҙлеге ул[11]:
- .
Цилиндрик координаталарҙа
[үҙгәртергә | сығанаҡты үҙгәртеү]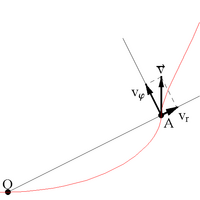
Цилиндрик координаталарҙа [11]:
арҡыры тиҙлек, — радиаль тиҙлек тип атала.
Сферик координаталарҙа
[үҙгәртергә | сығанаҡты үҙгәртеү]сферик координаталар системаһында [11]:
Яҫы хәрәкәтте тасуирлау өсөн ҡайһы берҙә поляр координаталар ҡулланыла, уны цилиндрик координаталарҙың ( const булғанда) йәки сферик координаталарҙың ( булғанда) айырым осрағы итеп ҡарап була.
Физик һәм координата тиҙлектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Аналитик механикала юғарыла килтерелгән һәм башҡа кәкре һыҙыҡлы координаталар дөйөмләштерелгән координаталар ролен уйнайҙар; есем торошоноң үҙгәреүе уларҙың ваҡытҡа бәйлелеге менән тасуирлана. Есем координаталарының ваҡыт буйынса сығарылмалары координата тиҙлектәре тип аталалар (уларҙың үлсәме м/c-тан айырмалы булырға мөмкин). Физик тиҙлек радиус-векторҙың ваҡыт буйынса сығарылмаһы була, ә уның төҙөүселәре һәр осраҡта ярашлы орт алдында торған бөтә аңлатма менән бирелә.
Тиҙлек менән бәйле ҡайһы бер төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]Классик механикала бер нисә дәүмәл тиҙлек аша күрһәтелә.
Импульс, йәки хәрәкәт миҡдары, — был нөктәнең механик хәрәкәтенең үлсәме, нөктәнең массаһының уның тиҙлегенә ҡабатландығы булараҡ билдәләнә
- .
Импульс вектор дәүмәл, уның йүнәлеше тиҙлек йүнәлеше менән тап килә. Йомоҡ система өсөн импульс һаҡланыу законы үтәлә.
Шулай уҡ механик системаның кинетик энергияһы тиҙлеккә бәйле. Абсолют ҡаты есем өсөн тулы кинетик энергияны ынтылышлы һәм әйләнмәле хәрәкәттең кинетик энергиялары суммалары күренешендә яҙырға мөмкин[12][13]:
бында — масса тела, — есемдең масса үҙәгенең тиҙлеге, — есемдең инерция моменты, — есемдең мөйөш тиҙлеге.
Тиҙлектең ваҡытта үҙгәреүе тиҙләнеш менән характерлана. Тиҙләнеш тиҙлектең дәүмәле буйынса үҙгәреүен дә (тангенциаль тиҙләнеш), шулай уҡ йүнәлеше буйынса үҙгәреүен дә (үҙәккә ынтылышлы тиҙләнеш) сағылдыра[14]:
бында — нөктә траекторияһының кәкрелек радиусы.
Тиҙлек өсөн Галилей һәм Лоренц үҙгәртеүҙәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Ньютондың классик механикаһында тиҙлектәр бер инерциаль иҫәпләү системаһынан икенсеһенә күскәндә Галилей үҙгәртеүҙәренә ярашлы үҙгәрәләр. Әгәр есемдең тиҙлеге иҫәпләү системаһында -ға тигеҙ булһа, ә иҫәпләү системаһының иҫәпләү системаһына ҡарата тиҙлеге -ға тигеҙ булһа, есемдең иҫәпләү системаһына күскәндә тиҙлеге[11]
- тигеҙ була
Яҡтылыҡ тиҙлегенә яҡын тиҙлектәр өсөн, Галилей үҙгәртеүҙәре дөрөҫ булмай башлай. системаһынан системаһына күскәндә тиҙлек өсөн Лоренц үҙгәртеүҙәрен ҡулланырға кәрәк[11]:
тиҙлеге системаһының күсәре буйлап йүнәлгән тип уйлағанда. Релятивистик булмаған тиҙлектәр сигендә Лоренц үҙгәртеүҙәре Галилей үҙгәртеүҙәренә ҡайтып ҡала.
Релятивистик механикала тиҙлек
[үҙгәртергә | сығанаҡты үҙгәртеү]Дүрт үлсәмле тиҙлек
[үҙгәртергә | сығанаҡты үҙгәртеү]Тиҙлек төшөнсәһенең дөйөмләштереүҙәренең береһе булып дүрт үлсәмле тиҙлек (релятивистстик механикала тора[11]). Махсус сағыштырмалылыҡ теорияһында һәр ваҡиғаға Минковский арауығының нөктәһе ярашлы ҡуйыла, уның өс координатаһы өс үлсәмле Евклид арауығының Декарт координаталары, ә дүртенсе ― ваҡыт координатаһы , бында ― яҡтылыҡ тиҙлеге, ― ваҡиға ваҡыты. Дүрт үлсәмле тиҙлек векторының компоненттары өс үлсәмле тиҙлек векторы проекцияларына түбәндәгесә бәйле.[11]:
Дүрт үлсәмле тиҙлек векторы ваҡытҡа оҡшаш вектор, йәғни яҡтылыҡ конусының эсендә ята[11].
Шулай уҡ дүртимпульс төшөнсәһе бар, уның ваҡытлы компоненты -ға тигеҙ (бында — энергия). Дүрт үлсәмле импульс өсөн түбәндәге тигеҙлек үтәлә[15]:
- ,
бында — дүрт үлсәмле тиҙлек.
«Йәһәтлек» төшөнсәһе
[үҙгәртергә | сығанаҡты үҙгәртеү]Релятивистик механикала киҫәксәнең йыһан һыҙығына тейеүсеһе һәм база иҫәпләү системаһында ваҡыт күсәре араһындағы мөйөш йәһәтлек тип атала ( тип тамғалана). Йәһәтлек түбәндәге формула менән күрһәтелә
бында — арктангенс, йәки гиперболик арктангенс. Тиҙлек яҡтылыҡ тиҙлегенә яҡынайғанда йәһәтлек сикһеҙлеккә ынтыла. Лоренц үҙгәртеүен ҡулланырға кәрәк булған тиҙлектән айырмалы рәүештә, йәһәтлек аддитив, йәғни
бында — иҫәпләү системаһының иҫәпләү системаһына ҡарата йәһәтлеге.
Ҡайһы бер тиҙлектәр
[үҙгәртергә | сығанаҡты үҙгәртеү]Космик тиҙлектәр
[үҙгәртергә | сығанаҡты үҙгәртеү]
Күк механикаһы Ҡояш системаһы есемдәренең һәм башҡа Күк есемдәренең тәртибен өйрәнә. Яһалма космик есемдәрҙең хәрәкәте астродинамикала өйрәнелә. Шул уҡ ваҡытта есемдәрҙең хәрәкәтенең бер нисә варианты ҡарала, уларҙың һәр береһенә билдәле бер тиҙлек бирергә кәрәк. Юлдашты түңәрәк орбитаға сығарыу өсөн уға беренсе космик тиҙлек бирергә кәрәк (мәҫәлән, Ерҙең яһалма юлдашы); преодолеть гравитацион тартыу көсөн еңеү өсөн икенсе космик тиҙлек бирергә кәрәк (мәҫәлән, Ерҙән осоролған, уның орбитаһынан сыҡҡан, ләкин Ҡояш системаһында ҡалған объект); өсөнсө космик тиҙлек, йондоҙҙоң тартыу көсөн еңеп, йондоҙ системаһын ташлап китеү өсөн кәрәк (мәҫәлән, Ерҙән осоролған, уның орбитаһынан һәм Ҡояш системаһы сиктәренән сыҡҡан объект); дүртенсе космик тиҙлек галактиканы ташлап китергә мөмкинлек бирәсәк.
Күк механикаһында Орбиталь тиҙлек тип есемдең система бариүҙәге (Барицентр — бариүҙәк — Ҡояш системаһының масса үҙәге) тирәләй әйләнеү тиҙлеген аңлайҙар.
Тулҡындарҙың таралыу тиҙлеге
[үҙгәртергә | сығанаҡты үҙгәртеү]Тауыш тиҙлеге
[үҙгәртергә | сығанаҡты үҙгәртеү]Тауыш тиҙлеге — мөхиттең һығылмалылығы һәм тығыҙлығы менән билдәләнгән һығылмалы тулҡындарҙың мөхиттә таралыу тиҙлеге. Тауыш тиҙлеге даими дәүмәл түгел һәм температураға (газдарҙа), тулҡындың таралыу йүнәлешенә (монокристалдарҙа) бәйле. Бирелгән тышҡы шарттарҙа ғәҙәттә тулҡын йышлығына һәм уның амплитудаһына бәйле түгел. Был үтәлмәгән осраҡта һәм тауыш тиҙлеге йышлыҡҡа бәйле булһа, тауыш дисперсияһы тураһында һүҙ бара. Беренсе тапҡыр Уильям Дерхам тарафынан үлсәнгән. Ҡағиҙә булараҡ, газдарҙа тауыш тиҙлеге шыйыҡсаларҙағынан бәләкәйерәк, ә шыйыҡсаларҙа тауыш тиҙлеге ҡаты есемдәрҙәгенән бәләкәйерәк, шуға күрә газды шыйығайтҡанда тауыш тиҙлеге арта.
Газ ағымының бирелгән нөктәләге ағым тиҙлегенең хәрәкәт итеүсе мөхиттә урындағы тауыштың таралыу тиҙлегенә нисбәте австрия ғалимы Эрнст Мах исеме буйынса Мах һаны тип атала. Ябайыраҡ әйткәндә, 1 атм баҫымында 1 Махҡа ярашлы тиҙлек (ерҙә диңгеҙ кимәлендә), тауыштың һауалағы тиҙлегенә тигеҙ була. Аппараттарҙың тауыш тиҙлегенә тиңләтелгән тиҙлек менән хәрәкәте тауыш барьеры тип аталған бер нисә күренеш оҙатыуында бара. 1,2-нән алып 5-кә тиклемге Мах тиҙлектәр тауыштан шәберәк тиҙлек тип атала, 5 Махтан юғарыраҡ тиҙлектәр — Гипертауышлы тиҙлек тип аталалар.
Яҡтылыҡ тиҙлеге
[үҙгәртергә | сығанаҡты үҙгәртеү]
Вакуумда яҡтылыҡ тиҙлеге — электромагнит тулҡындарының вакуумдағы таралыу тиҙлегенең абсолют дәүмәле. Ғәҙәти «c» латин хәрефе менән тамғалана ([це] тип уҡыла). Вакуумда яҡтылыҡ тиҙлеге — фундаменталь даими, инерциаль иҫәпләү системаһын (ИСО) һайлауға бәйле түгел. Ул Фундаменталь физичк даимиларға инә, айырым есемдәрҙе йәки ҡырҙарҙы ғына түгел, ә арауыҡ-ваҡыттың үҙсәнлектәрен тулыһынса характерлай. Хәҙерге заман ҡарашы буйынса, вакуумда яҡтылыҡ тиҙлеге — предельная скорость движения киҫәксәләр хәрәкәтенең һәм үҙ-ара тәьҫирләүеү таралыуының сикке тиҙлеге.
Яҡтылыҡ тиҙлеген иң теүәл үлсәү 299 792 458 ± 1,2 м/с эталон метр нигеҙендә 1975 йылда башҡарыла. Хәҙер метрҙың хәҙерге заман билдәләмәһе айҡанлы яҡтылыҡ тиҙлеге теүәл 299792458 м/с тип иҫәпләнә[16].
Гравитация тиҙлеге
[үҙгәртергә | сығанаҡты үҙгәртеү]Гравитация тиҙлеге — гравитацион йоғонтоноң, ҡуҙғыуҙарҙың һәм тулҡындарҙың таралыу тиҙлеге. Хәҙергә тиклем эксперименталь юл менән билдәләнмәгән көйө ҡала, әммә дөйөм сағыштырмалыҡ теориһына ярашлы яҡтылыҡ тиҙлеге менән тап килергә тейеш.
Тиҙлек рекордтары
[үҙгәртергә | сығанаҡты үҙгәртеү]Тиҙлек үлсәү берәмектәре
[үҙгәртергә | сығанаҡты үҙгәртеү]Һыҙыҡлы тиҙлек:
- Секундына метр, (м/с), СИ системаһының сығарылма берәмеге
- Сәғәтенә километр, (км/сәғ)
- узел (сәғәтенә диңгеҙ миле)
- Мах һаны, 1 Мах тауыш тиҙлегенә тигеҙ; Max n n тапҡыр шәберәк. Конкрет шарттарға бәйле берәмек булараҡ, өҫтәлмә билдәләнергә тейеш.
- Вакуумда яҡтылыҡ тиҙлеге (c менән тамғалана)
- секундына радиандарҙа, СИ һәм СГС системаларында ҡабул ителгән. Физик үлсәме 1/с.
- Секундына әйләнештәр (техникала)
- секундына градустар, секундына градтар
Тиҙлек берәмектәре араһында нисбәттәр
[үҙгәртергә | сығанаҡты үҙгәртеү]- 1 м/с = 3,6 км/сәғ
- 1 узел = 1,852 км/сәғ = 0,514 м/c
- Мах 1 ~ 330 м/c ~ 1200 км/сәғ (һауа булған шарттарға бәйле)
- c = 299 792 458 м/c
Тәбиғәттә һәм техникала тиҙлек
[үҙгәртергә | сығанаҡты үҙгәртеү]| Секундына метрҙарҙа | |
|---|---|
| Яҡтылыҡ тиҙлеге | 299 792 458 |
| Иң алыҫ галактикаларҙың хәрәкәт тиҙлеге | |
| Телевизор кинескобында электрондарҙың тиҙлеге | |
| Ҡояштың Галактика үҙәге тирәләй орбита буйлап хәрәкәт итеү тиҙлеге | |
| Ерҙең Ҡояш тирәләй орбита буйлап хәрәкәт итеү тиҙлеге | |
| Ерҙең яһалма юлдашының тиҙлеге | |
| Айҙың Ер тирәләй орбита буйлап хәрәкәт итеү тиҙлеге | |
| Пассажирҙар реактив самолётының максималь тиҙлеге | |
| 0 град С температураһында азот молекулаһының уртаса тиҙлеге | |
| Автомобилдең максималь тиҙлеге | [18] |
| Локомотивтың тимер юлда максималь тиҙлеге | |
| Ыласындың максималь осоу тиҙлеге | |
| Гепардтың тиҙлеге | |
| Кешенең 100 м дистанцияла тиҙлек рекорды | |
| Кешенең 50 километрға йәйәү йөрөүҙә тиҙлек рекорды | |
| Ташбаҡа тиҙлеге | |
| Ҡусҡар тиҙлеге |
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]| Тиҙлек Викимилектә |
- Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
- Старжинский В. М. Теоретическая механика. — М.: Наука, 1980. — 464 с.
- Яковлев В. И. Предыстория аналитической механики. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 328 с.
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ 3-8.1 // Quantities and units—Part 3: Space and time (ингл.) — 1 — ISO, 2006. — 19 p.
- ↑ 2,0 2,1 2,2 3-10.1 // Quantities and units — Part 3: Space and time, Grandeurs et unités — Partie 3: Espace et temps (ингл.) — 2 — ISO, 2019. — 11 p.
- ↑ 3-8.a // Quantities and units—Part 3: Space and time (ингл.) — 1 — ISO, 2006. — 19 p.
- ↑ 3-8.b // Quantities and units—Part 3: Space and time (ингл.) — 1 — ISO, 2006. — 19 p.
- ↑ Старжинский, 1980, с. 154
- ↑ Маркеев, 1990, с. 15—17
- ↑ Старжинский, 1980, с. 154—155
- ↑ Старжинский, 1980, с. 163
- ↑ Старжинский, 1980, с. 152
- ↑ Маркеев, 1990, с. 46—47
- ↑ 11,0 11,1 11,2 11,3 11,4 11,5 11,6 11,7 11,8 Скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
- ↑ Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
- ↑ Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь.. — 1983. Физическая энциклопедия
- ↑ Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
- ↑ Определение метра (инг.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
- ↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44
- ↑ FIA World Land Speed Records (ингл.). Federation Internationale de l'Automobile (10 июнь 2012). Дата обращения: 3 декабрь 2020.




















































































