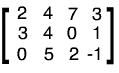Algebra lineare

La storia dell'algebra lineare moderna inizia fra il 1843 e il 1844. Nel 1843 William Rowan Hamilton (che ha introdotto il termine vettore) inventò i quaternioni. Nel 1844 Hermann Grassmann pubblicò il suo libro Die lineale Ausdehnungslehre. Arthur Cayley introdusse le matrici (2×2), una delle idee fondamentali dell'algebra lineare, nel 1857.

L'algebra lineare ha le sue origini nello studio dei vettori negli spazi cartesiani a due e a tre dimensioni. Un vettore, in questo caso, è un segmento orientato, caratterizzato da lunghezza (o magnitudine), direzione e verso. I vettori possono essere usati per rappresentare determinate entità fisiche come le forze, e possono essere sommati fra loro e moltiplicati per uno scalare, formando quindi il primo esempio di spazio vettoriale sui reali.

L'algebra lineare moderna è stata estesa per comprendere spazi di dimensione arbitraria o infinita. Uno spazio vettoriale di dimensione n è chiamato n-spazio. Molti dei risultati utili nel 2-spazio e nel 3-spazio possono essere estesi agli spazi di dimensione maggiore. Anche se molte persone non sanno visualizzare facilmente i vettori negli n-spazi, questi vettori o n-uple sono utili per rappresentare dati. Poiché i vettori, come n-uple, sono liste ordinate di n componenti, molte persone comprendono e manipolano i dati efficientemente in questa struttura. Ad esempio, in economia, si può creare e usare vettori 8-dimensionali (ottuple) per rappresentare il Prodotto Interno Lordo di 8 stati. Si può decidere di visualizzare il PIL di 8 stati per un particolare anno, ad esempio (Italia, Stati Uniti, Gran Bretagna, Francia, Germania, Spagna, Giappone, Australia), usando un vettore (v₁, v₂, v₃, v₄, v₅, v₆, v₇, v₈) dove il PIL di ogni stato è nella sua rispettiva posizione.

Uno spazio vettoriale è definito sopra un campo, come il campo dei numeri reali o il campo dei numeri complessi. Gli operatori lineari mappano elementi da uno spazio vettoriale su un altro (o su sé stesso), in modo che sia mantenuta la compatibilità con l'addizione e la moltiplicazione scalare definiti negli spazi vettoriali. L'insieme di tutte queste trasformazioni è anch'esso uno spazio vettoriale. Se è fissata una base per uno spazio vettoriale, ogni trasformazione lineare può essere rappresentata da una tabella chiamata matrice. Nell'algebra lineare si studiano quindi le proprietà delle matrici, e gli algoritmi per calcolare delle quantità importanti che le caratterizzano, quali il rango, il determinante e l'insieme dei suoi autovalori.

Uno spazio vettoriale (o spazio lineare), come concetto puramente astratto sul quale si provano teoremi, è parte dell'algebra astratta, e ben integrato in questo campo: alcuni oggetti algebrici correlati ad esempio sono l'anello delle mappe lineari da uno spazio vettoriale in sé, o il gruppo delle mappe lineari (o matrici) invertibili. L'algebra lineare gioca anche un ruolo importante in analisi, specialmente nella descrizione delle derivate di ordine superiore nell'analisi vettoriale e nella risoluzione delle equazioni differenziali.

Concludendo, si può dire semplicemente che i problemi lineari della matematica - quelli che esibiscono "linearità" nel loro comportamento - sono quelli più facili da risolvere, e che i problemi "non lineari" vengono spesso studiati approssimandoli con situazioni lineari. Ad esempio nell'analisi, la derivata è un primo tentativo di approssimazione lineare di una funzione. La differenza rispetto ai problemi non lineari è molto importante in pratica: il metodo generale di trovare una formulazione lineare di un problema, in termini di algebra lineare, e risolverlo, se necessario con calcoli matriciali, è uno dei metodi più generali applicabili in matematica.

La nozione più importante in algebra lineare è quella di spazio vettoriale. Uno spazio vettoriale è un insieme ${\displaystyle V}$  di elementi, detti vettori, aventi delle proprietà che li rendono simili ai vettori applicati in un punto fissato (l'origine) del piano o dello spazio.

Più precisamente, sono definite su ${\displaystyle V}$  un paio di operazioni binarie:^[1]

• due vettori ${\displaystyle v}$  e ${\displaystyle w}$  possono essere sommati, dando così luogo ad un nuovo vettore ${\displaystyle v+w}$ . Le proprietà della somma vettoriale sono associatività, commutatività, esistenza dell'elemento neutro, esistenza dell'elemento inverso;
• un vettore ${\displaystyle v}$  può essere riscalato, cioè moltiplicato per uno scalare, cioè un numero ${\displaystyle k}$ , dando così luogo ad un nuovo vettore ${\displaystyle kv}$ . le proprietà della moltiplicazione per scalare sono associatività, esistenza di un neutro;
• la somma vettoriale è distributiva rispetto al prodotto, mentre il prodotto è distributivo rispetto alla somma.

Il numero ${\displaystyle k}$  (detto scalare) appartiene ad un campo che viene fissato fin dall'inizio: questo può essere ad esempio il campo ${\displaystyle \mathbb {R} }$  dei numeri reali o il campo ${\displaystyle \mathbb {C} }$  dei numeri complessi.

Il piano cartesiano è l'esempio fondamentale di spazio vettoriale. Ogni punto del piano è in realtà identificato univocamente come una coppia ${\displaystyle (x,y)}$  di numeri reali. L'origine è il punto ${\displaystyle (0,0)}$ . Il punto ${\displaystyle (x,y)}$  può essere interpretato alternativamente come punto del piano o come vettore applicato nell'origine che parte da ${\displaystyle (0,0)}$  e arriva in ${\displaystyle (x,y)}$ .

Analogamente lo spazio cartesiano è formato da triple di punti ${\displaystyle (x,y,z)}$ . Più in generale, le ennuple di ${\displaystyle n}$  numeri reali

${\displaystyle (x_{1},\ldots ,x_{n})}$ 

formano uno spazio vettoriale che viene indicato con ${\displaystyle \mathbb {R} ^{n}}$ . Ancora più in generale, si può sostituire ${\displaystyle \mathbb {R} }$  con un altro campo ${\displaystyle K}$  e ottenere quindi lo spazio vettoriale ${\displaystyle K^{n}}$ .

Un'applicazione lineare è una funzione fra due spazi vettoriali

${\displaystyle f:V\to W}$ 

che sia compatibile con le operazioni definite su entrambi. Devono cioè valere le proprietà seguenti:

${\displaystyle f(v+w)=f(v)+f(w)}$ 

${\displaystyle f(kv)=kf(v).}$ 

per ogni coppia di vettori ${\displaystyle v,w}$  in ${\displaystyle V}$  e ogni scalare ${\displaystyle k}$ . I termini "applicazione", "funzione", "trasformazione", "mappa" e "omomorfismo" sono in questo contesto tutti sinonimi. Il termine "lineare" sta a indicare la compatibilità con le operazioni. Un'applicazione lineare manda necessariamente l'origine (di ${\displaystyle V}$ ) nell'origine (di ${\displaystyle W}$ ):

${\displaystyle f(0)=0.}$ 

Gli spazi ${\displaystyle V}$  e ${\displaystyle W}$  possono coincidere. In questo caso l'applicazione è più propriamente una trasformazione di ${\displaystyle V}$ , ovvero una funzione che sposta i punti di ${\displaystyle V}$ , chiamata anche endomorfismo. Una trasformazione di ${\displaystyle V}$  deve necessariamente tenere fissa l'origine O.

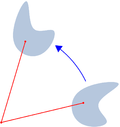
Molte trasformazioni del piano cartesiano o dello spazio che tengono fissa l'origine O sono lineari: tra queste, le rotazioni (intorno a O), le riflessioni rispetto ad una retta o un piano (passante per O), le omotetie (centrate in O) e le proiezioni (su una retta o piano passante per O).

Le applicazioni lineari compaiono in contesti molto differenti. Ad esempio, il funzionale

${\displaystyle \Psi (f)=\int _{0}^{1}f(x)}$ 

che associa ad una funzione ${\displaystyle f}$  il suo integrale è un'applicazione lineare

${\displaystyle \Psi :C([0,1])\to \mathbb {R} }$ 

dallo spazio ${\displaystyle C([0,1])}$  delle funzioni continue a valori reali in ${\displaystyle \mathbb {R} }$ .

Un punto ha dimensione zero, una retta ha dimensione uno, un piano ha dimensione due e uno spazio ha dimensione tre. L'algebra lineare permette di definire e trattare in modo rigoroso spazi di dimensione superiore alla terza. Lo spazio fondamentale di dimensione ${\displaystyle n}$  è lo spazio vettoriale delle ennuple, indicato con ${\displaystyle \mathbb {R} ^{n}}$ . Per ${\displaystyle n=2}$ , questo è l'usuale piano cartesiano.

Ogni spazio vettoriale ${\displaystyle V}$  ha una dimensione. Questa è definita in modo algebrico, come il numero di elementi in una base per ${\displaystyle V}$ : una base è un insieme di vettori che funge da sistema di riferimento per ${\displaystyle V}$ . Rigorosamente, una base è una successione

${\displaystyle {\mathcal {B}}=\{v_{1},\ldots ,v_{n}\}}$ 

di vettori indipendenti che generano lo spazio ${\displaystyle V}$ . Uno spazio vettoriale può avere anche dimensione infinita: gli spazi vettoriali di dimensione infinita sono spesso più complicati, e molti teoremi di algebra lineare richiedono come ipotesi che ${\displaystyle V}$  abbia dimensione finita.

Le nozioni di base e dimensione si applicano a ${\displaystyle \mathbb {R} ^{n}}$  (che ha dimensione ${\displaystyle n}$ ) e ai sottospazi ivi contenuti. Essendo però definite in modo puramente algebrico, si applicano anche in contesti molto differenti: ad esempio, le matrici ${\displaystyle m\times n}$  formano uno spazio vettoriale di dimensione ${\displaystyle mn}$ . I polinomi in una variabile formano uno spazio vettoriale di dimensione infinita: restringendo però il grado dei polinomi ad un certo valore massimo ${\displaystyle n}$  si ottiene uno spazio vettoriale di dimensione ${\displaystyle n+1}$ .

Due vettori ${\displaystyle v}$  e ${\displaystyle w}$  di uno spazio vettoriale possono essere sommati: il risultato è un vettore ${\displaystyle v+w}$ . Inoltre un vettore ${\displaystyle v}$  e uno scalare ${\displaystyle k}$  possono essere moltiplicati: il risultato è un vettore ${\displaystyle kv}$ . Nella definizione di spazio vettoriale non è però prevista un'operazione di prodotto fra due vettori.

In alcuni contesti è però utile aggiungere un'ulteriore operazione binaria fra vettori, che si comporti come un prodotto. Il risultato di questo prodotto può essere a sua volta un vettore o uno scalare. Nel primo caso, questa operazione si chiama prodotto vettoriale, e nel secondo prodotto scalare. L'operazione di prodotto vettoriale risulta però interessante solo in dimensione tre, mentre i prodotti scalari esistono (e sono utili) in tutte le dimensioni: per questo motivo questi ultimi sono molto più studiati.

Nella definizione di spazio vettoriale non è inoltre neppure prevista una nozione di lunghezza (equivalentemente, norma) per i vettori, né di angolo fra due di questi. Entrambe le nozioni di lunghezza e angolo risultano però definite se è fissato un opportuno prodotto scalare.^[2]

Un sistema di equazioni lineari è il dato di un certo numero ${\displaystyle k}$  di equazioni lineari in alcune variabili ${\displaystyle x_{1},\ldots ,x_{n}}$ . Usando le matrici e la moltiplicazione riga per colonne, un sistema può essere scritto in modo stringato nel modo seguente:

${\displaystyle Ax=b.}$ 

In questa espressione ${\displaystyle A}$  è una matrice ${\displaystyle k\times n}$ , ${\displaystyle x}$  è il vettore delle variabili ${\displaystyle x_{1}}$ , ..., ${\displaystyle x_{n}}$  e ${\displaystyle b}$  è un altro vettore formato da costanti.

L'algebra lineare fornisce molti algoritmi per determinare le soluzioni di un sistema lineare. Il legame fra i sistemi di equazioni e l'algebra lineare sta nel fatto che la matrice ${\displaystyle A}$  può essere interpretata come applicazione lineare da ${\displaystyle \mathbb {R} ^{n}}$  in ${\displaystyle \mathbb {R} ^{k}}$ : secondo questa interpretazione, le soluzioni ${\displaystyle x}$  sono esattamente le controimmagini di ${\displaystyle b}$ .

Il teorema di Rouché-Capelli fornisce un metodo per contare le soluzioni, senza necessariamente determinarle completamente.^[3] Nel caso in cui il sistema sia quadrato e abbia una sola soluzione, questa può essere scritta esplicitamente usando la regola di Cramer. Però tale soluzione teorica è praticamente utilizzabile solo per risolvere sistemi molto piccoli.^[4] Mentre i metodi di eliminazione (es. Gauss) e quelli iterativi (es. Gauss-Seidel) consentono di calcolare effettivamente le soluzioni di un sistema lineare, anche di grandi dimensioni.

In geometria analitica una retta o un piano sono descritti da sistemi di equazioni lineari: come si è appena visto, questi possono essere agevolmente studiati con gli strumenti dell'algebra lineare. Si possono quindi affrontare problemi quali le posizioni reciproche di due rette (o piani) nello spazio (che possono essere incidenti, paralleli o sghembi), e come queste variano per trasformazioni lineari.

Le coniche nel piano come ellisse, parabola e iperbole sono determinate da equazioni di secondo grado. Queste equazioni sono più complicate di quelle lineari, che sono di primo grado. Nonostante ciò, la classificazione delle coniche è realizzata in modo efficace con gli strumenti dell'algebra lineare, grazie a teoremi non banali quali il teorema spettrale e il teorema di Sylvester. Con gli stessi strumenti si classificano le quadriche nello spazio.

L'analisi matematica delle funzioni in una variabile non fa uso dell'algebra lineare. L'analisi delle funzioni in più variabili invece dipende fortemente da questo settore. La nozione di derivata è infatti estesa in più variabili a quella di differenziale: mentre la derivata è un semplice numero reale che indica la pendenza di una funzione in un punto, il differenziale è un'applicazione lineare, che indica sempre la "pendenza" di una funzione (a più variabili) in un punto.

Anche la nozione di derivata seconda si estende a più variabili: il risultato è una matrice detta matrice hessiana. Se questa matrice è simmetrica, ad esempio quando valgono le ipotesi del teorema di Schwarz, può essere agevolmente rappresentata come diagonale grazie al teorema spettrale.

Molti problemi dell'analisi funzionale, quali la ricerca di una soluzione per un'equazione differenziale, vengono affrontati analizzando un particolare spazio di funzioni. Uno spazio di funzioni è uno spazio vettoriale i cui elementi sono funzioni di un certo tipo (ad esempio continue, integrabili, derivabili... definite su un dominio fissato). Spazi di questo tipo sono generalmente di dimensione infinita, e sono dotati di alcune strutture aggiuntive, quali ad esempio un prodotto scalare (negli spazi di Hilbert), una norma (negli spazi di Banach) o una più generale topologia (negli spazi vettoriali topologici).

Esempi di spazi di funzioni includono gli spazi Lp e gli spazi di Sobolev.

La meccanica quantistica fa ampio uso dei teoremi più avanzati dell'algebra lineare. Il modello matematico usato in questo settore della fisica (formalizzato principalmente da Paul Dirac e John Von Neumann) descrive i possibili stati di un sistema quantistico come elementi di un particolare spazio di Hilbert e le grandezze osservabili (quali posizione, velocità, etc.) come operatori autoaggiunti. I valori che possono assumere queste grandezze quando vengono effettivamente misurate sono gli autovalori dell'operatore.

L'introduzione e l'uso di questi concetti matematici non banali nella fisica quantistica è stato uno dei maggiori stimoli allo sviluppo dell'algebra lineare nel XX secolo.

Una matrice è una tabella di numeri, come ad esempio:

${\displaystyle A={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}.}$ 

Le matrici sono utili in algebra lineare per rappresentare le applicazioni lineari. Questo viene fatto tramite la moltiplicazione riga per colonna. Ad esempio, la matrice descritta ${\displaystyle A}$  rappresenta una trasformazione del piano cartesiano ${\displaystyle \mathbb {R} ^{2}}$  in sé. Questa trasformazione manda il punto ${\displaystyle (x,y)}$  nel punto

${\displaystyle A{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}-y\\x\end{pmatrix}}.}$ 

Questa trasformazione non è nient'altro che una rotazione antioraria di 90º con centro l'origine.

La relazione fra matrici e applicazioni lineari è molto forte. Ogni applicazione lineare fra spazi vettoriali di dimensione ${\displaystyle m}$  e ${\displaystyle n}$  è descrivibile tramite una matrice associata di tipo ${\displaystyle n\times m}$ , purché in entrambi gli spazi vettoriali siano fissate delle basi. L'effetto di un cambiamento di base è codificato dalla matrice di cambiamento di base e la composizione di funzioni si traduce in una moltiplicazione fra matrici.

L'eliminazione di Gauss è un algoritmo che consente di ridurre una matrice in una forma più semplice tramite opportune mosse sulle righe. Questo algoritmo è usato principalmente per determinare le soluzioni di un sistema di equazioni lineari, ma ha anche applicazioni più interne all'algebra lineare: con l'eliminazione di Gauss si può determinare il rango, il determinante o l'inversa di una matrice, si può estrarre una base da un insieme di generatori.

Il determinante è un numero associato ad una matrice quadrata ${\displaystyle A}$ , generalmente indicato come ${\displaystyle \det A}$ . Da un punto di vista algebrico, il determinante è importante perché vale zero precisamente quando la matrice non è invertibile; quando non è zero, fornisce inoltre un metodo per descrivere la matrice inversa tramite la regola di Cramer.

Da un punto di vista geometrico, il determinante fornisce molte informazioni sulla trasformazione associata ad ${\displaystyle A}$ : il suo segno (sui numeri reali) indica se la trasformazione mantiene l'orientazione dello spazio, ed il suo valore assoluto indica come cambiano le aree degli oggetti dopo la trasformazione.

Per caratterizzare un endomorfismo è utile studiare alcuni vettori, chiamati autovettori. Geometricamente, un autovettore è un vettore che non cambia direzione. Da un punto di vista algebrico, si tratta di un vettore ${\displaystyle v}$  tale che

${\displaystyle Av=\lambda v}$ 

per qualche scalare ${\displaystyle \lambda }$ , detto autovalore. L'endomorfismo è particolarmente semplice da descrivere se è diagonalizzabile: geometricamente, questo vuol dire che esiste una base di autovettori; algebricamente, vuol dire che l'endomorfismo può essere rappresentato tramite una matrice diagonale, come ad esempio

${\displaystyle {\begin{pmatrix}2&0\\0&-1\end{pmatrix}}.}$ 

Gli autovalori possono essere trovati agevolmente calcolando il polinomio caratteristico della matrice associata, definito come

${\displaystyle p(\lambda )=\det(A-\lambda I).}$ 

Gli autovalori di ${\displaystyle A}$  sono precisamente le radici di questo polinomio. Gli autovettori si organizzano in sottospazi vettoriali chiamati autospazi. Quando lo spazio vettoriale è uno spazio di funzioni, l'autovalore è una particolare funzione, chiamata autofunzione.

Un endomorfismo diagonalizzabile è rappresentabile in modo agevole tramite una matrice diagonale. Non tutti gli endomorfismi sono però diagonalizzabili: ad esempio, una rotazione antioraria del piano cartesiano ${\displaystyle \mathbb {R} ^{2}}$  di angolo ${\displaystyle \theta }$  è rappresentata dalla matrice

${\displaystyle {\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}}$ 

che (per ${\displaystyle \theta }$  diverso da 0 e ${\displaystyle \pi }$ ) non ha autovalori né autovettori, e quindi a maggior ragione non può essere diagonalizzabile. Un altro esempio di matrice non diagonalizzabile è la seguente

${\displaystyle {\begin{pmatrix}1&1\\0&1\end{pmatrix}}.}$ 

Se il campo considerato è però il campo ${\displaystyle \mathbb {C} }$  dei numeri complessi, è comunque possibile rappresentare l'endomorfismo tramite una matrice che assomiglia il più possibile ad una matrice diagonale, come nel secondo esempio mostrato. Questa rappresentazione, detta forma canonica di Jordan, caratterizza completamente gli endomorfismi. Esiste un'analoga rappresentazione nel campo reale, leggermente più complicata.

Similmente ad un endomorfismo, anche un prodotto scalare può essere rappresentato da una matrice quadrata. Anche in questo contesto, la forma più semplice da trattare è quella in cui la matrice risulta essere diagonale, e questo accade precisamente quando si fissa una base ortogonale.

A differenza degli endomorfismi, in questo contesto è sempre possibile trovare una matrice diagonale. In altre parole, per qualsiasi prodotto scalare è possibile trovare basi ortogonali. Se il prodotto scalare è definito positivo, un algoritmo efficiente a questo scopo è l'ortogonalizzazione di Gram-Schmidt. Per prodotti scalari più generali si può usare l'algoritmo di Lagrange.

Il teorema della dimensione (o del rango) è un teorema che mette in relazione le dimensioni del nucleo e dell'immagine di un'applicazione lineare ${\displaystyle f}$ , secondo la formula:

${\displaystyle \dim \operatorname {Im} (f)+\dim \operatorname {Ker} (f)=n.}$ 

Qui Im e Ker denotano immagine e nucleo, mentre ${\displaystyle n}$  è la dimensione del dominio di ${\displaystyle f}$ . Questo risultato è anche chiamato teorema del rango, perché tradotto nel linguaggio delle matrici assume la forma seguente:

${\displaystyle \operatorname {rk} (A)+\operatorname {null} (A)=n.}$ 

Qui rk e null indicano rispettivamente il rango e l'indice di nullità di una matrice ${\displaystyle A}$  del tipo ${\displaystyle m\times n}$ .

Il teorema di Rouché-Capelli dà alcune informazioni sull'insieme delle soluzioni di un generico sistema lineare:

${\displaystyle Ax=b.}$ 

Il teorema afferma due cose:

• il sistema ha soluzione se e solo se le matrici ${\displaystyle A}$  e ${\displaystyle (A|b)}$  hanno lo stesso rango ${\displaystyle r}$ ;
• se ci sono soluzioni, queste formano un sottospazio affine di dimensione ${\displaystyle n-r}$ , dove ${\displaystyle n}$  è il numero di incognite (cioè il numero di colonne di ${\displaystyle A}$ ).

In particolare, il numero di soluzioni può essere solo zero, uno o infinito (se le equazioni sono a coefficienti reali o complessi).

Il teorema è generalmente usato per determinare rapidamente se un sistema ammette una o più soluzioni: non può però essere usato per determinarle esplicitamente. Uno strumento per questo scopo è il metodo di eliminazione di Gauss.

La formula di Grassmann mette in relazione le dimensioni di vari sottospazi, definiti a partire da due sottospazi ${\displaystyle V}$  e ${\displaystyle W}$  entrambi contenuti uno spazio fissato ${\displaystyle U}$ . La formula è la seguente:

${\displaystyle \dim V+\dim W=\dim(V+W)+\dim(V\cap W).}$ 

Nell'espressione compaiono i sottospazi ottenuti come somma e intersezione di ${\displaystyle V}$  e ${\displaystyle W}$ .

Il teorema spettrale fornisce una condizione forte di diagonalizzabilità per alcuni endomorfismi, detti simmetrici o autoaggiunti (a volte il termine operatore è usato come sinonimo di endomorfismo). La nozione di endomorfismo simmetrico (o operatore autoaggiunto) dipende dalla presenza di un fissato prodotto scalare definito positivo (o hermitiano se si usano spazi vettoriali complessi). Il teorema spettrale asserisce che un tale endomorfismo ha una base ortonormale formata da autovettori.

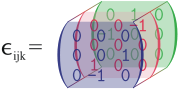
I metodi dell'algebra lineare sono stati estesi ad altre branche della matematica, grazie al loro successo. Nella teoria dei moduli si sostituisce il campo degli scalari con un anello. L'algebra multilineare si occupa dei problemi che mappano linearmente 'molte variabili' in un numero differente di variabili, portando inevitabilmente al concetto di tensore. Nella teoria spettrale degli operatori si riescono a gestire matrici di dimensione infinita applicando l'analisi matematica in una teoria non puramente algebrica. In tutti questi casi le difficoltà tecniche sono maggiori. Inoltre, l'algebra lineare viene a essere fondamentale per ambiti riguardanti l'ottimizzazione, in particolare la ricerca operativa.

• (IT) Ciro Ciliberto (1994): Algebra lineare, Boringhieri
• (IT) Serge Lang (2014): Algebra lineare, Boringhieri
• (EN) Steven Roman (1992): Advanced linear algebra, Springer, ISBN 0-387-97837-2
• (EN) de Boor, Carl, Applied Linear Algebra, (University of Wisconsin-Madison, 2002).
• (EN) Rife, Susan A, Matrix Algebra.^{[collegamento interrotto]} (Naval Postgraduate School, Monterey, California, 1996)
• (EN) Delatorre, Anthony R. e Cooke, William K., Matrix Algebra.^{[collegamento interrotto]} (Naval Postgraduate School, Monterey, California, 1998)
• (EN) Beezer, Rob, A First Course in Linear Algebra, licenza GFDL.
• (EN) J. H. M. Wedderburn Lectures on Matrices (American Mathematical Society, Providence, 1934) ISBN 0-8218-3204-2
• (EN) Fearnley-Sander, Desmond, Hermann Grassmann and the Creation of Linear Algebra, American Mathematical Monthly 86 (1979), pp. 809 – 817.
• (EN) Grassmann, Hermann, Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert, O. Wigand, Leipzig, 1844.
• (EN) Shafarevich, Igor R., Remizov, Alexey O. Linear Algebra and Geometry, Springer, 2012, ISBN 978-3-642-30993-9

• Algoritmo di Lagrange
• Autovalore e autovettore
• Base (algebra lineare)
• Determinante
• Dimensione (spazio vettoriale)
• Eliminazione di Gauss
• Forma canonica di Jordan
• Formula di Grassmann
• Matrice
• Ortogonalizzazione di Gram-Schmidt
• Prodotto scalare
• Sistema di equazioni lineari
• Spazio vettoriale
• Teorema della dimensione
• Teorema di Rouché-Capelli
• Teorema spettrale
• Trasformazione lineare

•   Wikibooks contiene testi o manuali sull'algebra lineare
•   Wikizionario contiene il lemma di dizionario «algebra lineare»
•   Wikiversità contiene risorse sull'algebra lineare
•   Wikimedia Commons contiene immagini o altri file sull'algebra lineare

• Dario A. Bini e Luca Gemignani, ALGEBRA LINEARE, in Enciclopedia Italiana, VII Appendice, Istituto dell'Enciclopedia Italiana, 2006.  
• àlgebra lineàre, su sapere.it, De Agostini.  
• algebra lineare, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.  
• (EN) Mark Andrew Ronan, linear algebra, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.  
• (EN) Eric W. Weisstein, Algebra lineare, su MathWorld, Wolfram Research.  
• (EN) Algebra lineare, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.  
• (EN) Linear Algebra Toolkit.
• (EN) Linear Algebra Workbench: moltiplica e inverte matrici, risolve sistemi, trova autovalori, ecc.